- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Нахождение экстремумов функции; авторы: Курушин П.Д., Дубоделов С.И.
Содержание
- 2. Экстре́мум (лат. extremum — крайний) в математике —
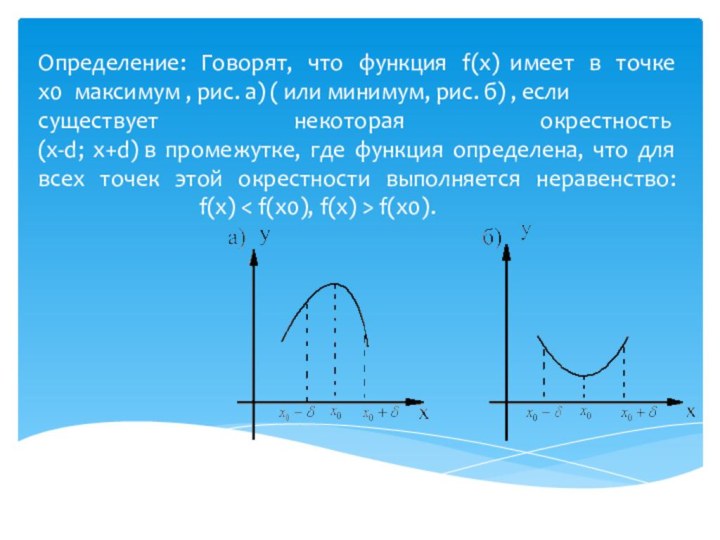
- 3. Определение: Говорят, что функция f(x) имеет в точке
- 4. Необходимое условие экстремума (Теорема Ферма): Пусть функция определена
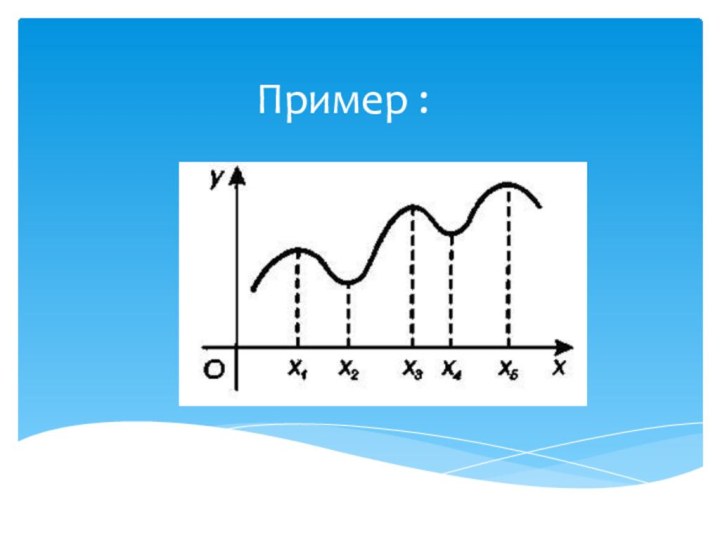
- 5. Пример :
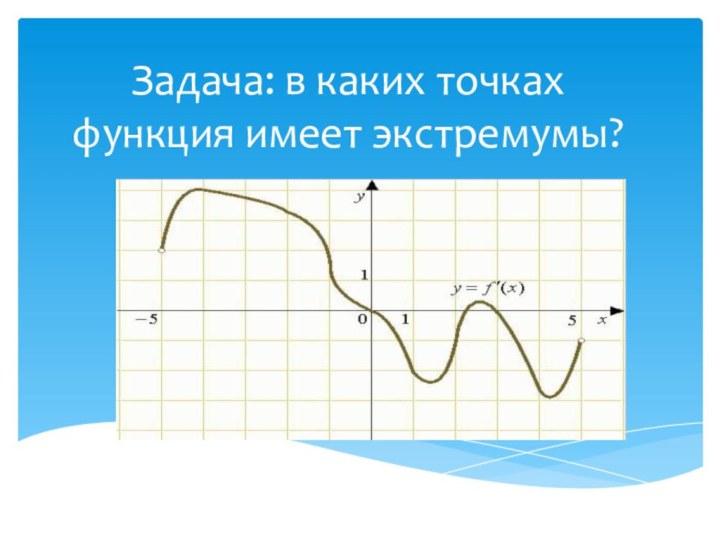
- 6. Задача: в каких точках функция имеет экстремумы?
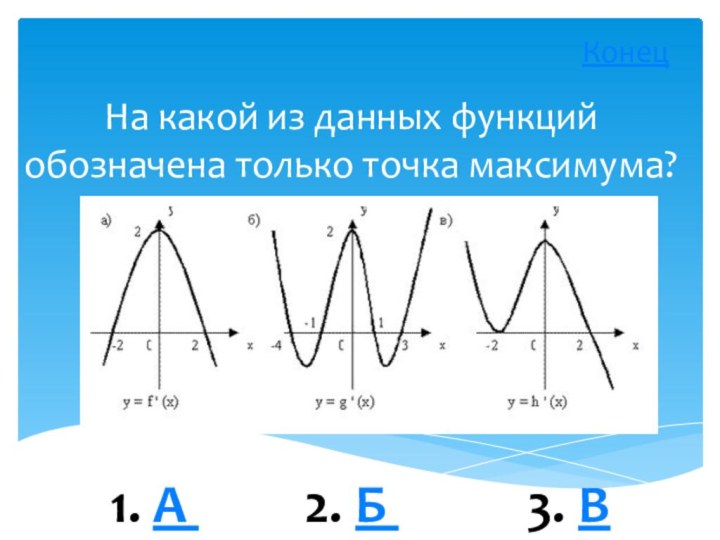
- 7. На какой из данных функций обозначена только
- 8. Правильно!!Назад
- 9. Неправильно!Назад
- 10. Скачать презентацию
- 11. Похожие презентации
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.