уравнение может быть переписано в виде a1x+b1
= с1y=k1x+b1
y=k2x+b2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




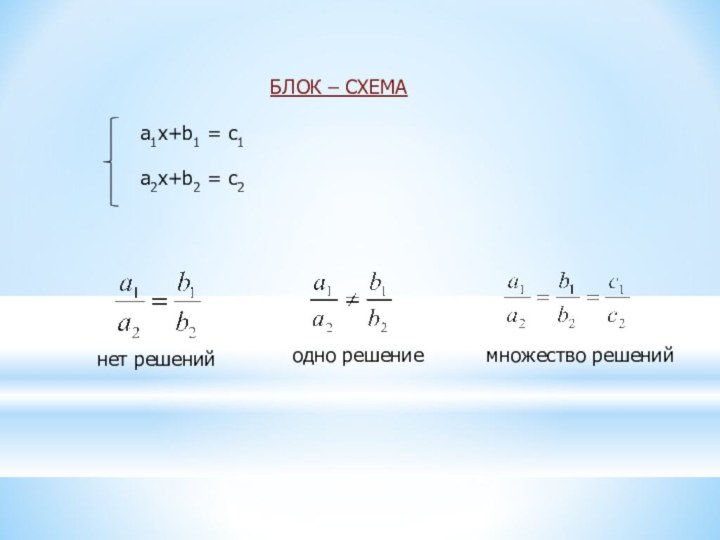






y=k1x+b1
y=k2x+b2
ах-6у = 14:
а)имеет бесконечное множество решений;
б) имеет единственное решение?
б) Система имеет единственное решение, если:
2 способ: выразим из первого уравнения х, х=1,5у+3,5 и подставим во второе уравнение, получим (1,5а-6)у=14-3,5а, тогда
а=4, 0у=0, система имеет бесконечное
множество решений,а≠4, у=
, система имеет единственное решение.
Ответ:
а) если а = 4, то система имеет бесконечное множество решений;
б) если а ≠4, то решение единственное.
то х=-2 является
решением следующей системы:
у=(4-а)х+а,
у=ах+2;
тогда имеем:
у=(4-а)(-2)+а,
у=а(-2)+2;
у=-8+3а,
у=-2а+2;
-8+3а=-2а+2; 5а=10; а=2.
Найдем ординату у, подставив х и а в любое уравнение системы:у=2 • (-2)+ 2,
у = -2.
Ответ:
- 2
а) Найдите b и к.
б)Найдите точку пересечения этих графиков.
b = 4, а графики пересекаются в некоторой точке (х; 0). Получим систему:
2х + 4 = 0,
kх-4 = 0;
х = -2,
к = -2.
В результате точка пересечения графиков у = кх-4 и
у = 2х + b (-2;0).
Ответ:
а) b= 4, к = -2; б) (-2; 0).