Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике Диагональ сыры

Содержание

Мақсаты: Қарапайым фигура ретінде үшбұрышты алып, фигураларды зерттейміз. Олардың диагональдарының қасиеттерін қолдана отырып, аудандарын табамыз. Сонымен қатар өмірдегі маңызын анықтаймыз.
Диагональ сыры Мақсаты: Қарапайым фигура ретінде үшбұрышты алып, фигураларды зерттейміз. Олардың диагональдарының қасиеттерін Кіріспе Нүкте, түзу және кесінділерді қосу арқылы геометриялық фигуралар: - үшбұрыш: тік бұрышты, 1.Үшбұрыш Үшбұрыш - ең Егер АВС үшбұрышының ВЕ биссектрисасын жүргізсек, онда АВЕ және ЕВС Үшбұрыштың ауданын құрамындағы үшбұрыштар ауданынан тауып көрейік. ТөртбұрышТөртбұрыш -төрт нүктеден тұратын және оларды тізбектей қосатын кесінділерден тұратын фигура.Сонда үш Параллелограмм Параллелограмм – қарама-қарсы қабырғалары параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш. Егер АВСD параллелограммның диагональ жүргізсек, онда параллелограмның АВС және СДА үшбұрыштарынан тұрады.Екінші Параллелограммның ауданын мына формуламен табуға болады Тіктөртбұрыш Барлық бұрыштары тік болып келетін параллелограммды тіктөртбұрыш дейміз. Тіктөртбұрыштың диагональдары тең болады. Екі ABC CDA үшбұрышты қосу арқылы ABCD тіктөртбұрыш пайда болады. AC диагоналі. Ромб Барлық қабырғалары тең параллелограмм ромб деп аталады.Ромбының диагональдары өзара перпендикуляр ЕсепБер: ромб, =6см, =8смТ/к: SШешуі: = *a*b ,a= ТрапецияЕкі қабырғасы ғана параллель болатын дөңес төртбұрыш трапеция деп аталады.Қарсы жатқан төбелерін Есеп. Бер: a= 8м, b= 6м, h= 3м Т/к: S Шешуі: КөпбұрыштарКөпбұрыш – жазықтықтағы кез келген тұйық сынық Есеп. Бер: a=2 Т/к: S Шешуі: = Фигуралар үшбұрыштардан тұрады 1.ПараллелепипедАВЕКМТН Егер призманың табаны параллелограмм болса, онда Есеп. Бер: a=2м Т/к: S Шешуі: = 12* Дастархан үлгісін безендіреміз Әшекей бұйымдарын жасаймыз Құрылыста жаңа ғимараттар Адам сұлулығы үшін Киім үлгісі Үй безендіруде
Слайды презентации

Слайд 2 Мақсаты: Қарапайым фигура ретінде үшбұрышты алып, фигураларды

Мақсаты: Қарапайым фигура ретінде үшбұрышты алып, фигураларды зерттейміз. Олардың диагональдарының

зерттейміз. Олардың диагональдарының қасиеттерін қолдана отырып, аудандарын табамыз. Сонымен

қатар өмірдегі маңызын анықтаймыз.

Слайд 3 Кіріспе

Кіріспе Геометрия геометриялық фигуралардың қасиеттері

Геометрия
геометриялық фигуралардың қасиеттері

туралы ғылым



Планиметрия
геометрияның жазықтықтағы
фигураларды зерттейді

Стереометрия
геометрияның кеңістіктегі
фигураларды зерттейді

Слайд 4 Нүкте, түзу және кесінділерді қосу арқылы геометриялық фигуралар:

Нүкте, түзу және кесінділерді қосу арқылы геометриялық фигуралар: - үшбұрыш: тік

- үшбұрыш: тік бұрышты, теңбүйірлі, теңқабырғалы, сүйір бұрышты, доғалбұрышты;

- төртбұрыш: параллелограмм, тіктөртбұрыш, ромб, трапеция;
- көпбұрыштар: бесбұрыш, алтыбұрыш.
- дөңгелек



Слайд 5

1.Үшбұрыш Үшбұрыш - ең қарапайым көпбұрыш. Үш

1.Үшбұрыш
Үшбұрыш - ең қарапайым көпбұрыш.
Үш нүктеден,

үш қабырғадан және үш
бұрыштан тұрады немесе бір түзу
бойында жатпайтын үш нүктені қосатын
кесінділер шектейтін жазықтық бөлігі .
Үшбұрыштардың түрлері:
теңқабырғалы, теңбүйірлі,
сүйірбұрышты, тік бұрышты,
доғал бұрышты.

Слайд 6 Егер АВС үшбұрышының ВЕ биссектрисасын жүргізсек,

Егер АВС үшбұрышының ВЕ биссектрисасын жүргізсек, онда АВЕ және ЕВС

онда АВЕ және ЕВС үшбұрыштарынан тұратындығын көреміз. Мысалға АВЕ

үшбұрышын қарастырайық. АВЕ үшбұрышынан ЕК биссектрисасын түсірсек, АВС үшбұрышының өзі бірнеше үшбұрыштардан тұратындығын көреміз.

А

В

С

Е



А

В

Е

К

К

Е

В

М

Слайд 7 Үшбұрыштың ауданын құрамындағы үшбұрыштар ауданынан тауып көрейік.

Үшбұрыштың ауданын құрамындағы үшбұрыштар ауданынан тауып көрейік.

бұл үлкен үшбұрыш құрамындағы кіші үшбұрыш ауданы, үлкен үшбұрыш ауданын табу үшін кіші үшбұрыш аудандарын қосамыз.






Есеп.
Бер: АВС. а=34.5 дм, h=12.6дм.
Т/к:S
Шешуі:


Тексеріп көрейік ,


Жауабы: S= 217.34(ДМ2)





Е




































А

С

В

Слайд 8 Төртбұрыш
Төртбұрыш -төрт нүктеден тұратын және оларды тізбектей қосатын

ТөртбұрышТөртбұрыш -төрт нүктеден тұратын және оларды тізбектей қосатын кесінділерден тұратын фигура.Сонда

кесінділерден тұратын фигура.Сонда үш нүкте бір түзу бойында жатпауы

тиіс, ал оларды қосатын кесінділер қиылыспау керек. Төртбұрыш түрлері: тіктөртбұрыш, параллелограмм, ромб,
трапеция, квадрат.



Слайд 9 Параллелограмм
Параллелограмм – қарама-қарсы қабырғалары

Параллелограмм Параллелограмм – қарама-қарсы қабырғалары параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш.

параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш.





Слайд 10 Егер АВСD параллелограммның диагональ жүргізсек, онда параллелограмның АВС

Егер АВСD параллелограммның диагональ жүргізсек, онда параллелограмның АВС және СДА үшбұрыштарынан

және СДА үшбұрыштарынан тұрады.Екінші диагональ жүргізсек, параллелограмм AOB, BOC,

COD, AOD теңбүйірлі үшбұрыштан тұратындығын көреміз.



А

В

С

D

O

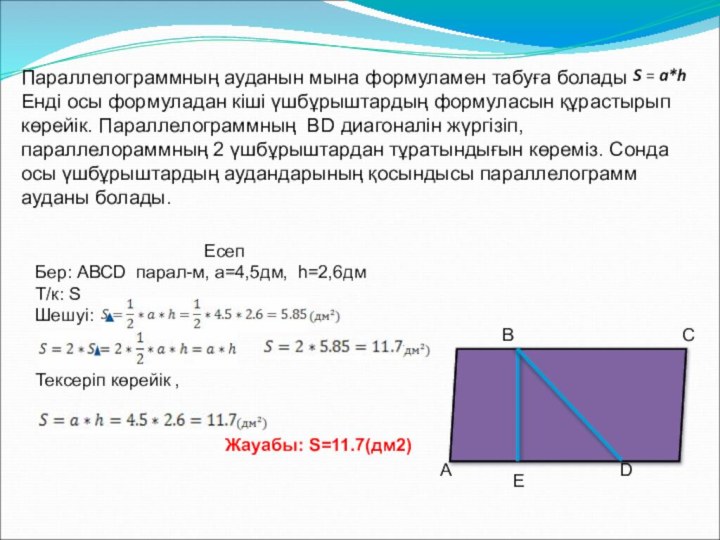
Слайд 11 Параллелограммның ауданын мына формуламен табуға болады

Параллелограммның ауданын мына формуламен табуға болады Енді осы

Енді осы формуладан кіші үшбұрыштардың

формуласын құрастырып көрейік. Параллелограммның BD диагоналін жүргізіп, параллелораммның 2 үшбұрыштардан тұратындығын көреміз. Сонда осы үшбұрыштардың аудандарының қосындысы параллелограмм ауданы болады.

S = a*h

Есеп
Бер: АВСD парал-м, а=4,5дм, h=2,6дм
Т/к: S
Шешуі:


Тексеріп көрейік ,


Жауабы: S=11.7(дм2)










А

В

С

D

Е











Слайд 12 Тіктөртбұрыш
Барлық бұрыштары тік болып

Тіктөртбұрыш Барлық бұрыштары тік болып келетін параллелограммды тіктөртбұрыш дейміз. Тіктөртбұрыштың диагональдары тең болады.

келетін параллелограммды тіктөртбұрыш дейміз. Тіктөртбұрыштың диагональдары тең болады.





Слайд 13 Екі ABC CDA үшбұрышты қосу арқылы ABCD тіктөртбұрыш

Екі ABC CDA үшбұрышты қосу арқылы ABCD тіктөртбұрыш пайда болады. AC

пайда болады. AC диагоналі. Енді осы тіктөртбұрыш ауданын табайық.

Негізгі формуланы 2 ге бөлгенде 1 үшбұрыштың ауданы шығады.

Есеп.
Бер:тіктөртбұрыш, а=16см, в=25см
Т/к: S
Шешуі:



Тексеріп көрейік ,


Жауабы: S=400(см2)
















А

В

С

D

Слайд 14 Ромб
Барлық қабырғалары тең параллелограмм ромб деп

Ромб Барлық қабырғалары тең параллелограмм ромб деп аталады.Ромбының диагональдары өзара перпендикуляр

аталады.Ромбының диагональдары өзара перпендикуляр және олар бұрыштарының биссектрисалары болады.



Слайд 15 Есеп
Бер: ромб, =6см, =8см
Т/к: S
Шешуі:

ЕсепБер: ромб, =6см, =8смТ/к: SШешуі: = *a*b ,a= *

= *a*b ,
a= * a=

*6=3(см), b= * b= *8=4(см)
= *3*4=6( )
=4* =4*6=24( )
Тексеріп көрейік , S= ,
= =24
Жауабы: S=24( )
















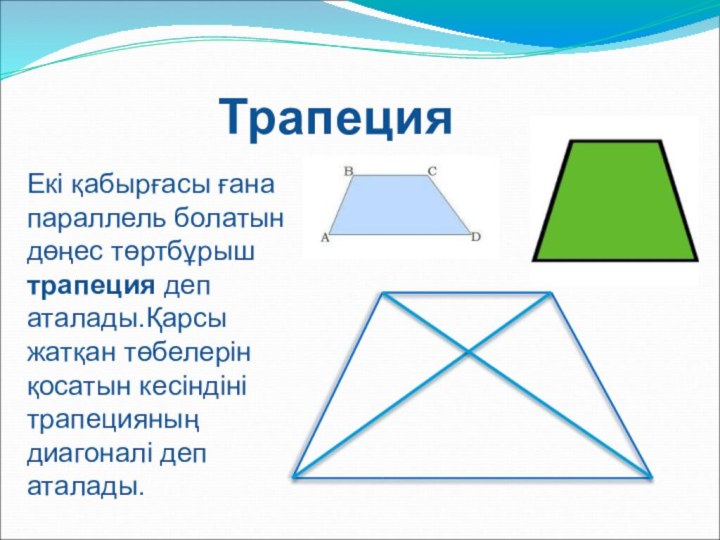
Слайд 16 Трапеция
Екі қабырғасы ғана параллель болатын дөңес төртбұрыш трапеция

ТрапецияЕкі қабырғасы ғана параллель болатын дөңес төртбұрыш трапеция деп аталады.Қарсы жатқан

деп аталады.Қарсы жатқан төбелерін қосатын кесіндіні трапецияның диагоналі деп

аталады.


Слайд 17
Есеп.
Бер: a= 8м, b= 6м, h= 3м

Есеп. Бер: a= 8м, b= 6м, h= 3м Т/к: S Шешуі:

Т/к: S
Шешуі: = *a*h ,

= *8*3=12( )
= *6*3=9( ) =12+9=21( )
 
Тексеріп көрейік, = *h , = *3=21( )
Жауабы: S=21( )









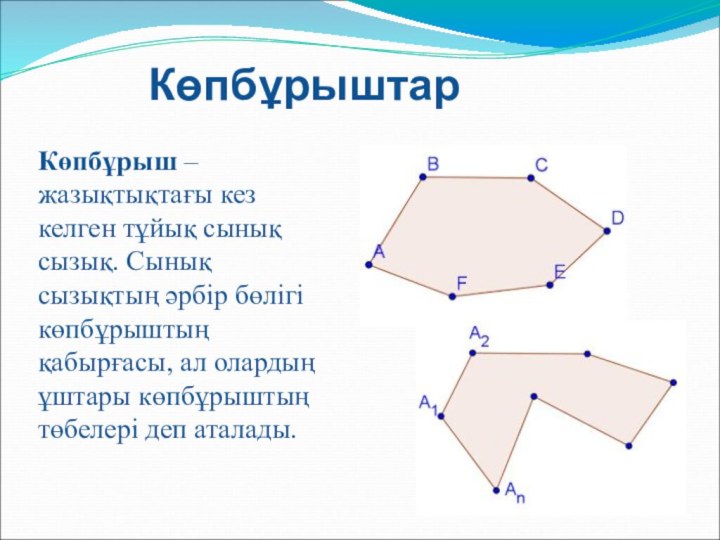
Слайд 18 Көпбұрыштар
Көпбұрыш – жазықтықтағы

КөпбұрыштарКөпбұрыш – жазықтықтағы кез келген тұйық сынық сызық. Сынық

кез келген тұйық сынық сызық. Сынық сызықтың әрбір бөлігі

көпбұрыштың қабырғасы, ал олардың ұштары көпбұрыштың төбелері деп аталады.  




Слайд 19
Есеп.
Бер: a=2
Т/к: S
Шешуі:

Есеп. Бер: a=2 Т/к: S Шешуі: =

= =

=
= 6
Жауабы: S=6








Слайд 20 Фигуралар үшбұрыштардан тұрады

Фигуралар үшбұрыштардан тұрады

Слайд 21 1.Параллелепипед

А
В
Е
К
М
Т
Н
Егер призманың

1.ПараллелепипедАВЕКМТН Егер призманың табаны параллелограмм болса, онда ол параллелепипед

табаны параллелограмм болса, онда ол параллелепипед деп аталады.
Параллелепипедтің жақтарының

диагоналін жүргізіп, параллелепипед жақтарын 2 үшбұрышқа бөлуге болады.

Слайд 22
Есеп.
Бер: a=2м
Т/к: S
Шешуі:

Есеп. Бер: a=2м Т/к: S Шешуі: = 12*

= 12* =

*a*a=
= =2 =12*2=24( )
=6* =6* =24( )
Жауабы: S=24( )













Слайд 23 Дастархан үлгісін безендіреміз

Дастархан үлгісін безендіреміз

Слайд 24 Әшекей бұйымдарын жасаймыз


Әшекей бұйымдарын жасаймыз

Слайд 25 Құрылыста жаңа ғимараттар

Құрылыста жаңа ғимараттар

Слайд 26 Адам сұлулығы үшін









Адам сұлулығы үшін

Слайд 27 Киім үлгісі



Киім үлгісі

Слайд 28 Үй безендіруде




Үй безендіруде
  • Имя файла: prezentatsiya-po-matematike-diagonal-syry.pptx
  • Количество просмотров: 353
  • Количество скачиваний: 0
- Предыдущая Презентация Викторина для 5-х классов В гостях у сказки
Следующая - Презентация по технологии на тему Конструирование фартука (5 класс)

Похожие презентации

Презентация по математике на тему: Применение производной в профессиональной деятельности Презентация по математике на тему: Применение производной в профессиональной деятельности 183
Обобщающий урок по теме: Системы линейных уравнений Обобщающий урок по теме: Системы линейных уравнений 76
../// ../// 134
Презентация по математике на тему Логарифмы в жизни и в быту(10-11класс). Презентация по математике на тему Логарифмы в жизни и в быту(10-11класс). 174
Формула разности квадратов 7 класс Формула разности квадратов 7 класс 162
Тригонометрические формулы Тригонометрические формулы 169
Геометриялық прогрессия 9 класс Геометриялық прогрессия 9 класс 556
Показательная функция Показательная функция 178
Презентация по математике на тему Задачи по теории вероятности. Подготовка к итоговой аттестации Презентация по математике на тему Задачи по теории вероятности. Подготовка к итоговой аттестации 154
Презентация 7 сыныпқа математика пәнінен Презентация 7 сыныпқа математика пәнінен 348
Презентация Обзор УМК по математике Презентация Обзор УМК по математике 185
Презентация пот алгебре 8 класс Презентация пот алгебре 8 класс 156
Презентация по алгебре на тему Произведение одночленов - 2 урок (7 класс) Презентация по алгебре на тему Произведение одночленов - 2 урок (7 класс) 183
Готовимся к ОГЭ по алгебре Готовимся к ОГЭ по алгебре 140
Степенная функция Степенная функция 170
Логарифмы. Логарифмическая функция Логарифмы. Логарифмическая функция 153
Урок Логарифмы Урок Логарифмы 139
Задачи по теории вероятности Задачи по теории вероятности 152
Презентация по алгебре на тему: Квадратичная функция (7 класс) Презентация по алгебре на тему: Квадратичная функция (7 класс) 155
Вычисление пределов Вычисление пределов 146
Подготовка к ОГЭ. Игра по алгебре Подготовка к ОГЭ. Игра по алгебре 144
Презентация к уроку алгебры в 10 классе Четные и нечетные функции Презентация к уроку алгебры в 10 классе Четные и нечетные функции 175
Презентация ро алгебре Решение задач Презентация ро алгебре Решение задач 187
Задачи для устной работы по геометрии Задачи для устной работы по геометрии 137
Презентация по алгебре на тему: Теорема Виета Презентация по алгебре на тему: Теорема Виета 191
Презентация к уроку алгебры решение уравнений Презентация к уроку алгебры решение уравнений 240
Презентация по математике на тему Решение уравнений (7 класс) Презентация по математике на тему Решение уравнений (7 класс) 161
Урок математики 10 класс Урок математики 10 класс 178
Решение квадратных уравнений по формуле Решение квадратных уравнений по формуле 152
Презентация к уроку в 9классе квадратичная функция и квадратные уравнения Презентация к уроку в 9классе квадратичная функция и квадратные уравнения 149