- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определение числовой функции
Содержание
- 2. Определение 1Если даны числовое множество Х и
- 3. Пишут:y=f(x), x∊Xнезависимая переменная или аргументзависимая переменнаяОбласть определения
- 4. Определение 2Если дана функция y=f(x), x∊X и
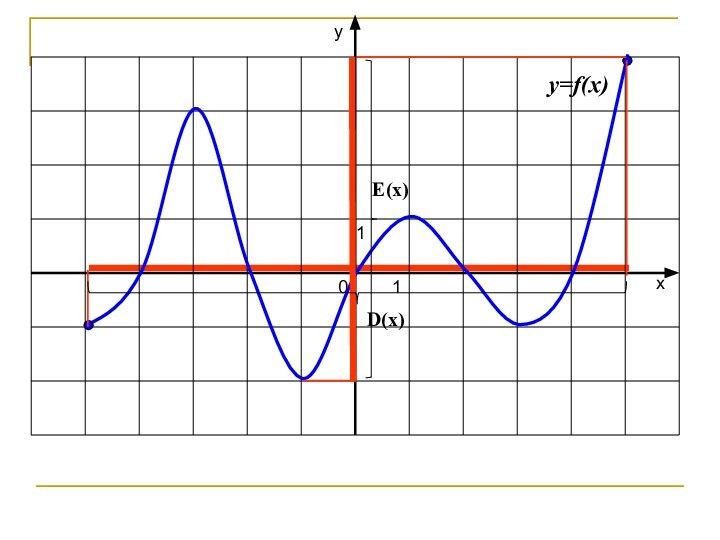
- 5. y=f(x)Е(х)D(х)
- 6. Способы задания функцииЗаключается в задании таблицы отдельных
- 7. Например:
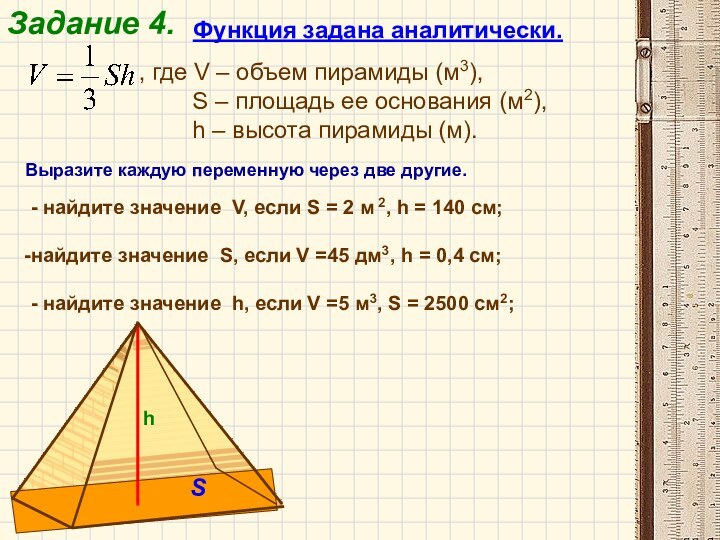
- 8. Аналитический способЧаще всего закон, устанавливающий связь между
- 9. Графический способГрафический способ задания функции не всегда
- 10. Например:
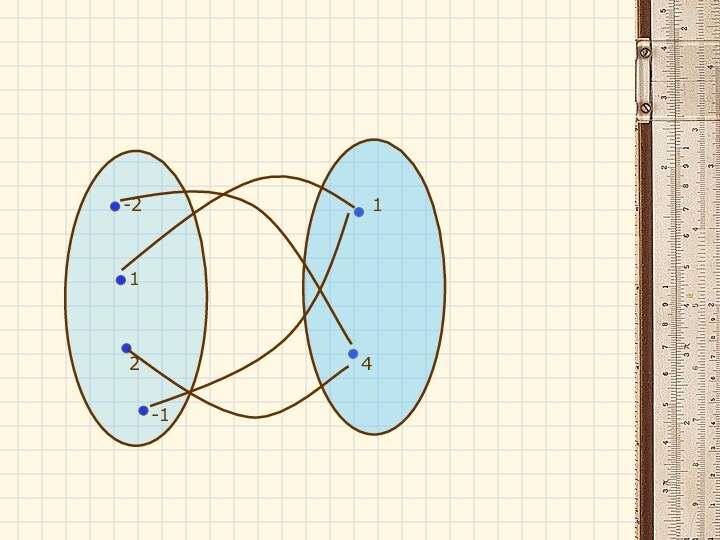
- 11. С помощью графовВо многих задачах теории графов,
- 12. -221-114
- 13. Словесная формулировкаПример: функция у = f(х) задана
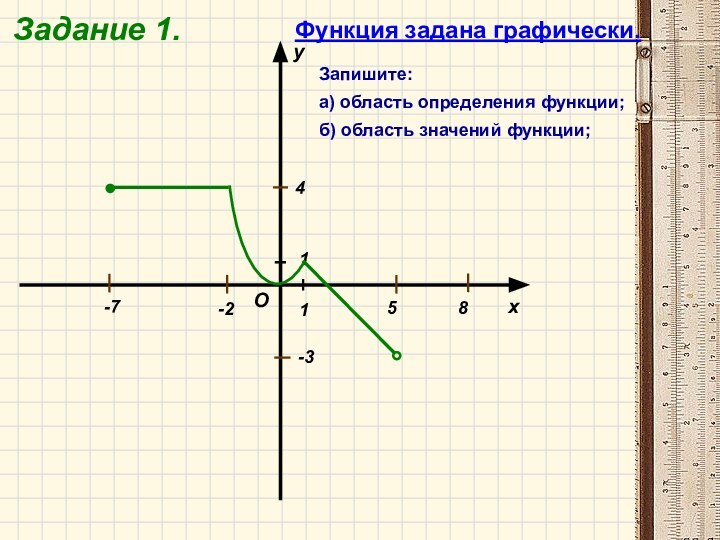
- 14. Задание 1.-7-285-34Функция задана графически.Запишите:а) область определения функции;б) область значений функции;
- 15. Задание 2.
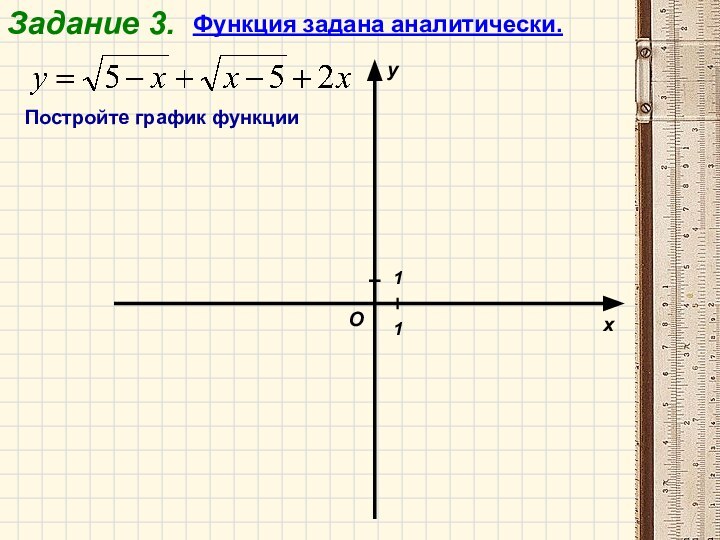
- 16. Задание 3.Функция задана аналитически.Постройте график функции
- 17. Скачать презентацию
- 18. Похожие презентации
Определение 1Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число y, то говорят, что задана функция y=f(x) с областью определения Х.










Слайд 3
Пишут:
y=f(x), x∊X
независимая переменная или аргумент
зависимая переменная
Область определения функции
– это все значения, которые может принимать переменная х.
Обозначается D(f).Область значений функции – это все значения, которые может принимать переменная y. Обозначается E(f).
Слайд 4
Определение 2
Если дана функция y=f(x), x∊X и на
координатной плоскости xOy отмечены все точки вида (x;y), то
множество этих точек называют графиком функции y=f(x), x∊X.
Слайд 6
Способы задания функции
Заключается в задании таблицы отдельных значений
аргумента и соответствующих им значений функции. Применяется в том
случае, когда область определения функции является дискретным конечным множеством.Табличный способ
Слайд 8
Аналитический способ
Чаще всего закон, устанавливающий связь между аргументом
и функцией, задается посредством формул. Такой способ задания функции
называется аналитическим.Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Например, у = 2х + 1,
у = 2х²,
у = ¼х + 8 и т. д.
Слайд 9
Графический способ
Графический способ задания функции не всегда дает
возможность точно определить численные значения аргумента. Однако он имеет
большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Слайд 11
С помощью графов
Во многих задачах теории графов, графы
удобно описывать матрицами, выделяя на матрицу смежности и матрицу
инцидентности.Полный граф – система, в которой между любой парой процессов существует прямая линия связи.
Слайд 13
Словесная формулировка
Пример: функция у = f(х) задана на
множестве всех неотрицательных чисел, с помощью следующего правила: каждому
числу х ≥ 0 ставится в соответствии первый знак после запятой в десятичной записи числа х.
Слайд 14
Задание 1.
-7
-2
8
5
-3
4
Функция задана графически.
Запишите:
а) область определения функции;
б) область
значений функции;
Слайд 15
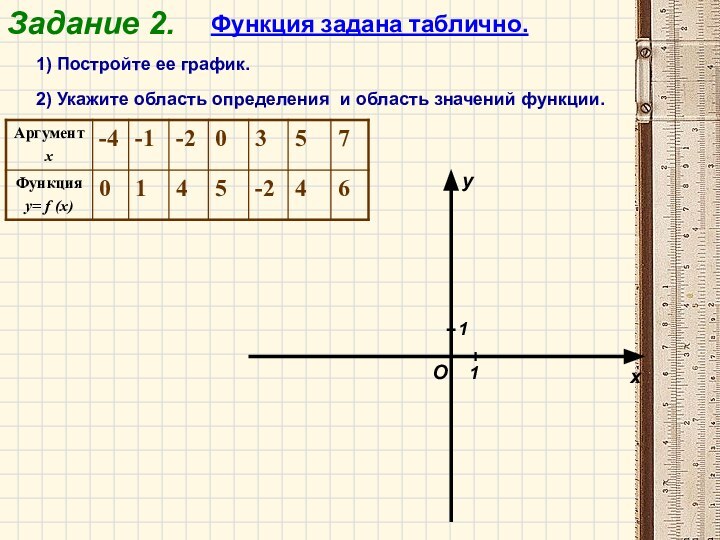
Задание 2.
Функция задана таблично.
1) Постройте ее график.
2) Укажите область определения и область значений функции.
x
y
O
1
1





























