tg α, ctg α.
Формулы приведения.
Косинус суммы и разности двух
углов.Синус суммы и разности двух углов.
5. Сумма и разность синусов и косинусов.
Содержание
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








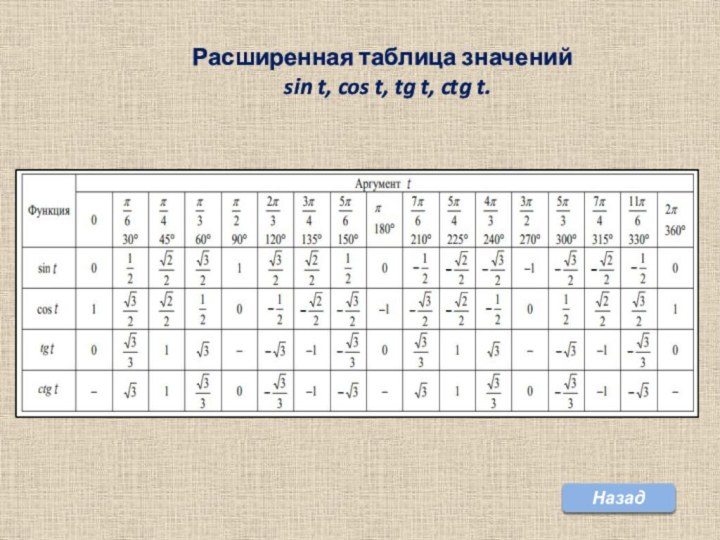

Содержание
б) tg 60° · sin 60° ·ctg 30°;
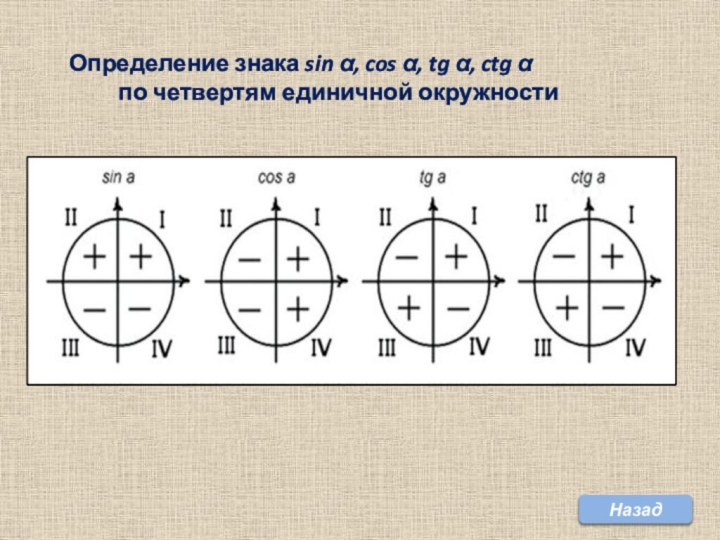
2. Углом какой четверти является угол α, если:
а) cos α > 0 и sin α > 0; б) sin α > 0 и tg α > 0;
в) ctg α > 0 и sin α < 0; в) sin α < 0 и cos α < 0.
3. Определите знак выражения(оперируйте знаками по четвертям):
а) sin 100°· cos 300°; б) cos 320°· ctg 17 °;
в) sin 190°· tg 200°; г) tg 170°· cos 400°.
Решение:
=> sin α = sin β =
Так как α находится в первой четверти, то применяя таблицу значений синусов, угол α = 30°.
Но имеется еще и второй угол β
(II четверть).
Из равенства треугольников ONB и OMA следует, что α = γ.
Поэтому: β = 180°- γ = 150°.
Следствие. ВСЕГДА α = γ.
tg (-α) = - tg α
ctg (-α) = - ctg α
Назад
где
1
2
3
4
5
где
где
sin (α + 2πk) = sin α
cos (α + 2πk) = cos α
tg (α + πk) = tg α
ctg (α + πk) = ctg α
6
7
где