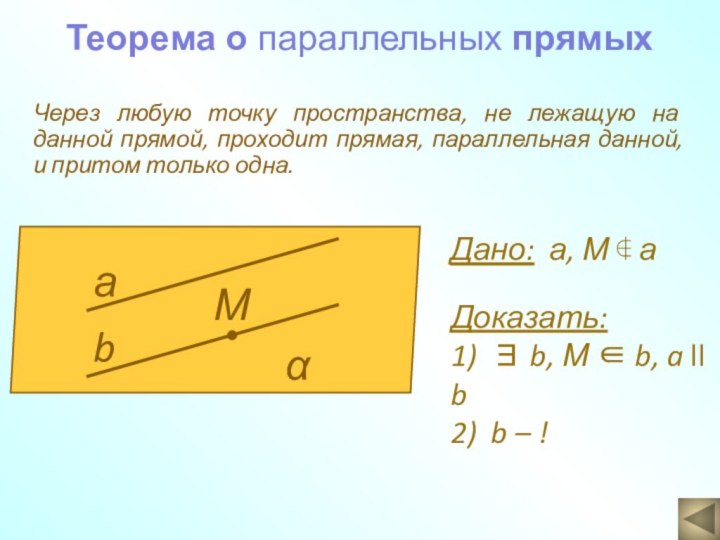
лежащую на данной прямой, проходит прямая, параллельная данной, и
притом только одна.а
b
α
М
Дано: а, М а
Доказать:
1) ∃ b, М b, a ll b
2) b – !
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

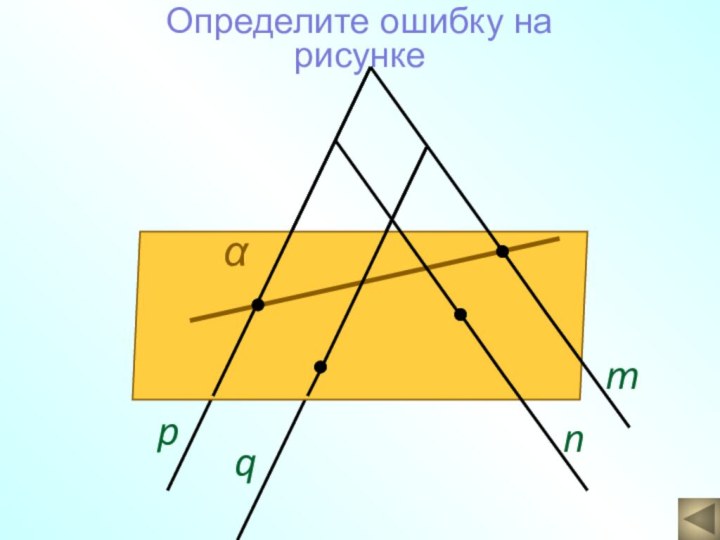
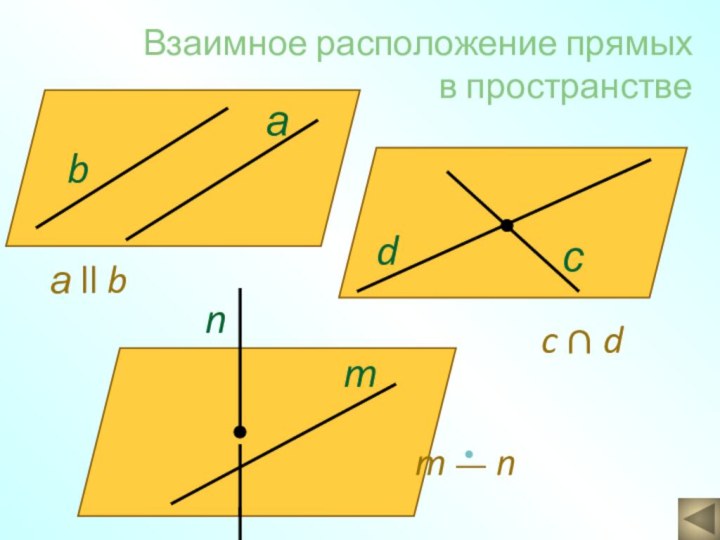
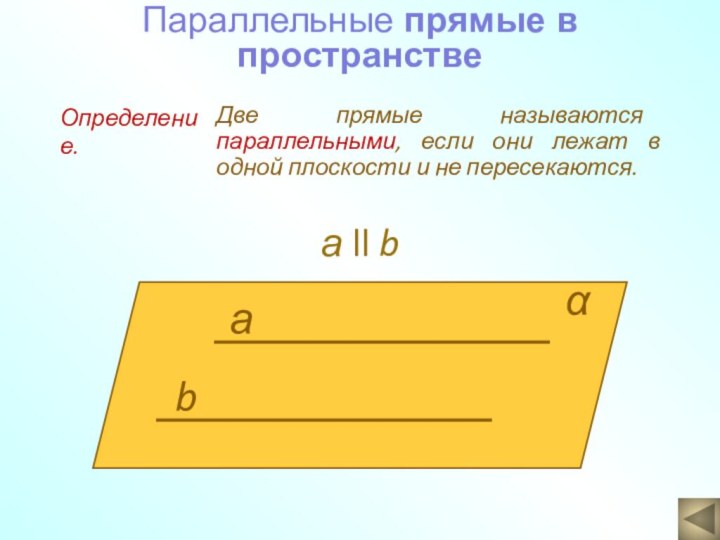


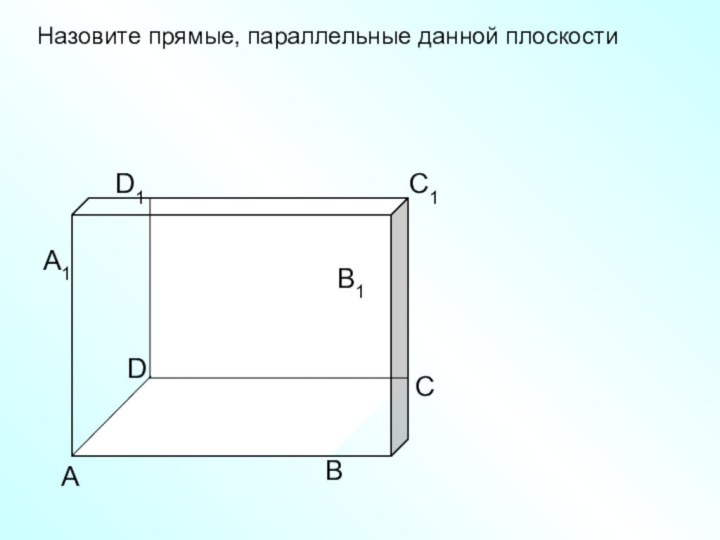



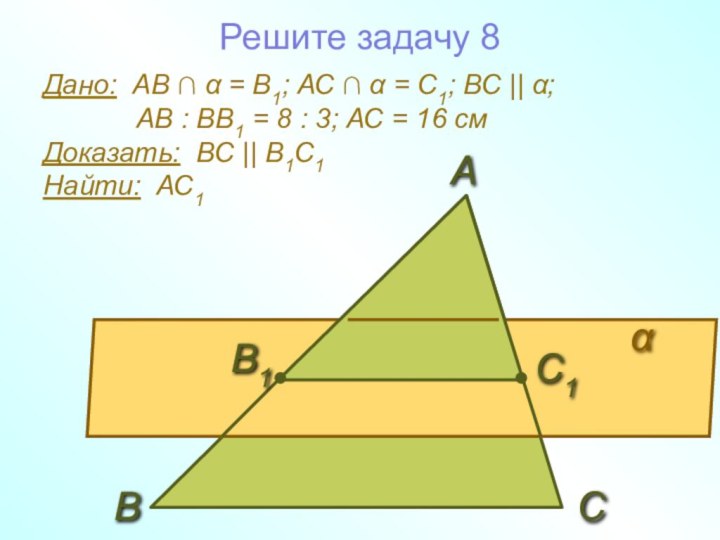
а
b
α
М
Дано: а, М а
Доказать:
1) ∃ b, М b, a ll b
2) b – !
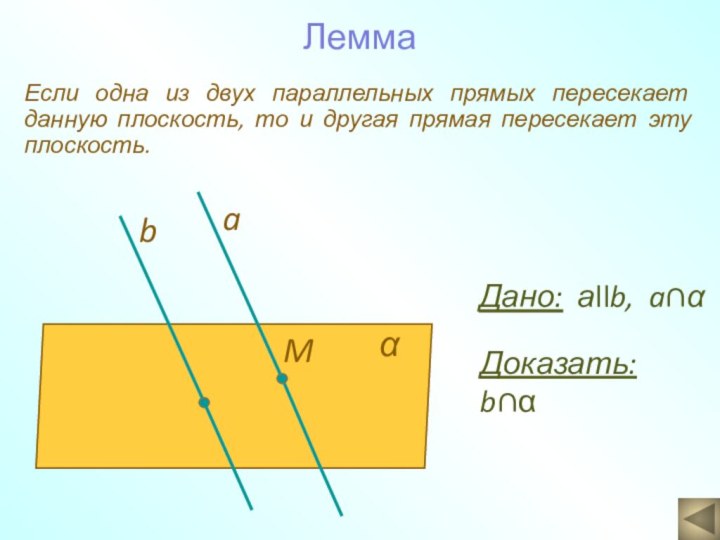
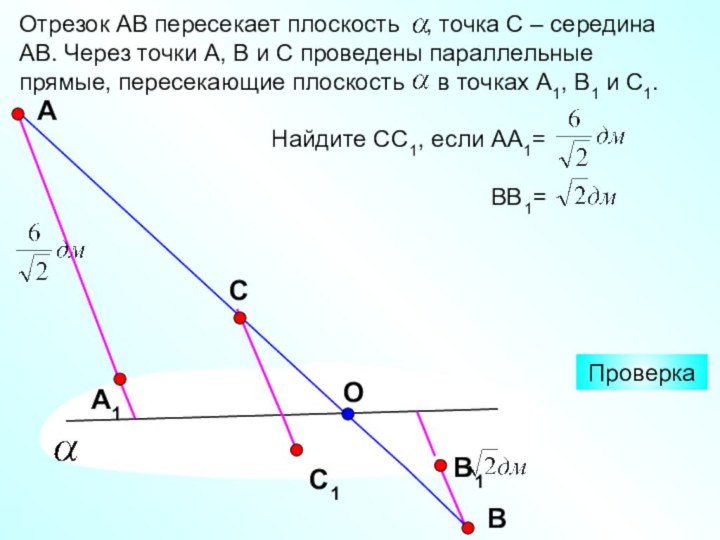
Доказать: b∩α
b
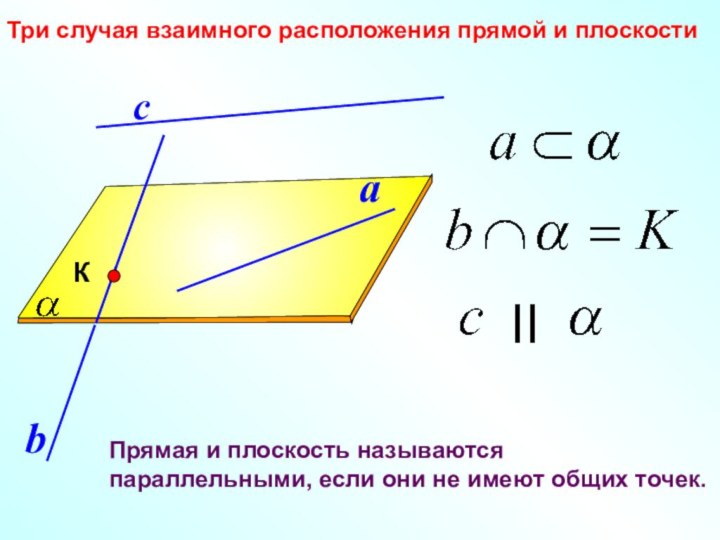
c
К
Применим способ от противного
α
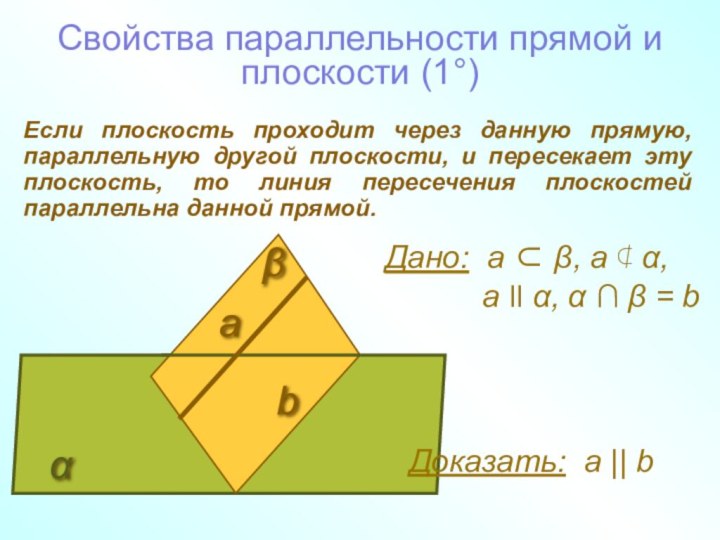
Дано: a β, a α,
а ll α, α ∩ β = b
Доказать: а || b
а
β
b
α
Дано: а || α, а || b
Доказать: b || α,
b α
а
b
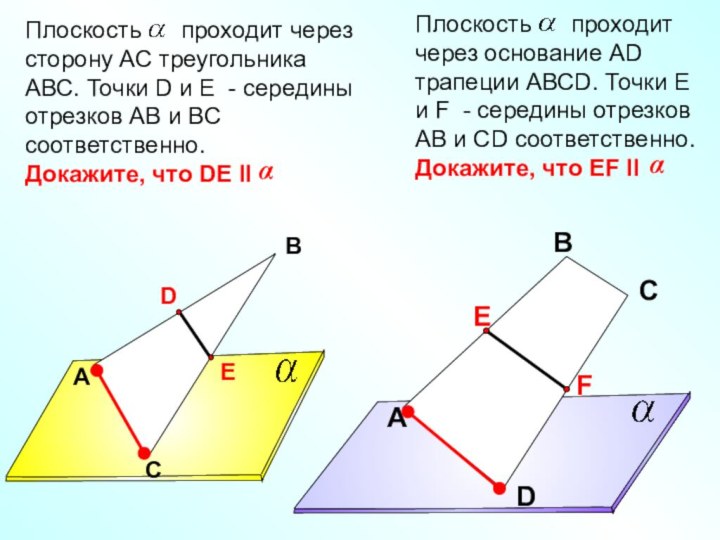
Свойства параллельности прямой и плоскости (2°)
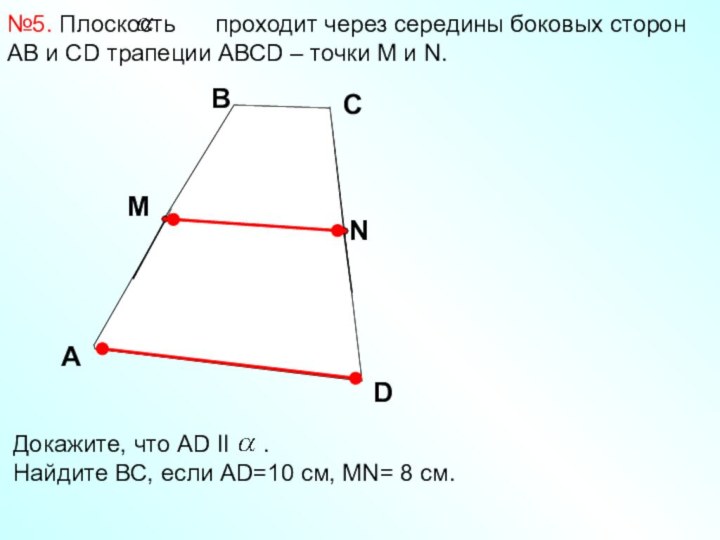
A
D
С
M
N
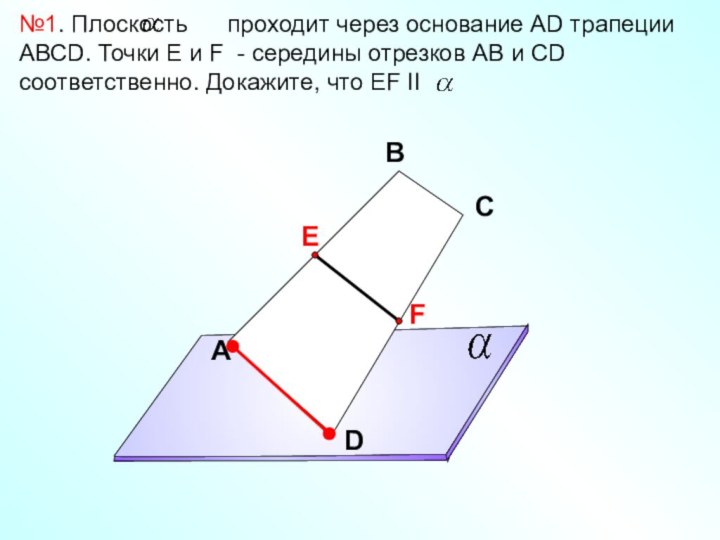
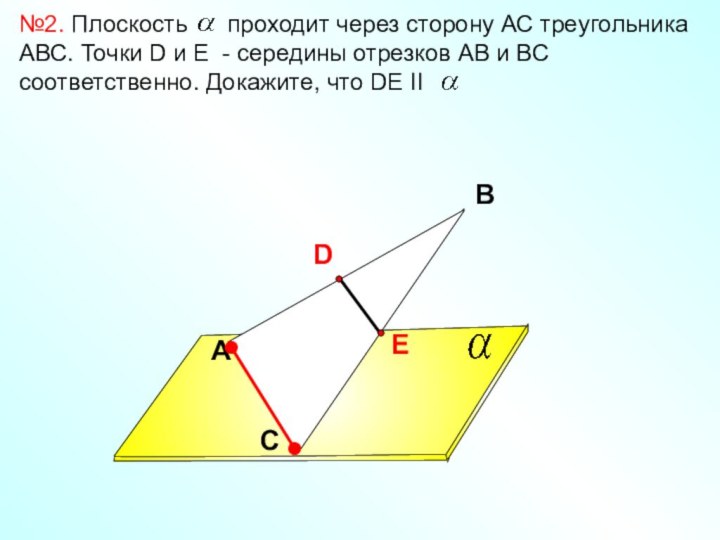
Докажите, что АD II .
Найдите ВС, если АD=10 см, MN= 8 см.
B
A
D
С
C
B
M
N
a