- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему График линейной функции
Содержание
- 2. График линейной функции
- 3. Цели урока:Обучающие:1. Учить строить график линейной функции;2.
- 4. Воспитательные:Формирование организационных умений; умений самоконтроля.
- 5. Развивающие:Развитие логического мышления учащихся через использование ими
- 6. План:Актуализация знаний.Изучение новой темы.Закрепление: устные упражнения, задачи на построение графиков.Задание на дом. Подведение итога урока.
- 7. 1. В координатной плоскости отметьте точки: А(0;6),
- 8. Тема урока:Линейная функция и её график
- 9. Составьте выражение к условию задачи:На складе 500
- 10. Выполнить задание.На складе было 500 тонн угля.
- 11. Турист проехал на автобусе 15 километров от
- 12. Что общего в полученных выражениях?Сделайте вывод.Определение линейной
- 13. Какие из функций 1. 2.3.4.5.6.7
- 14. Найдите значение линейной функции у=2х-1 при заданном
- 15. Вывод с записью в тетради.Графиком линейной функции является прямая линия.
- 16. Сколько точек нужно взять, чтобы построить прямую?Для
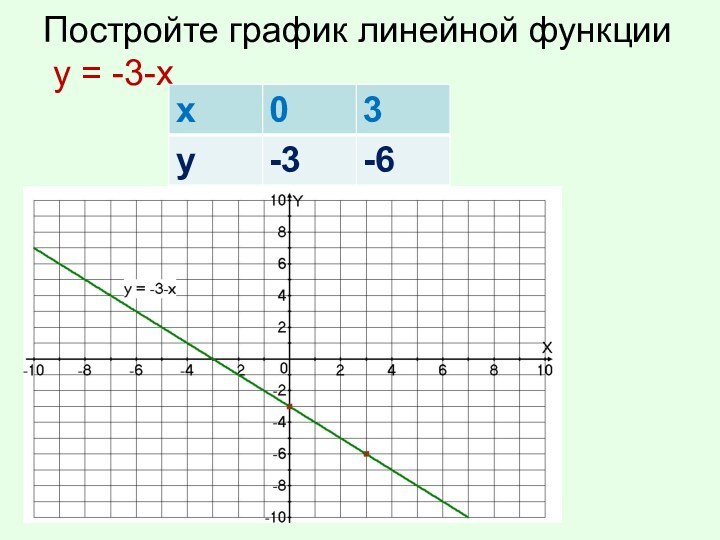
- 17. Постройте график линейной функции у = -3-х
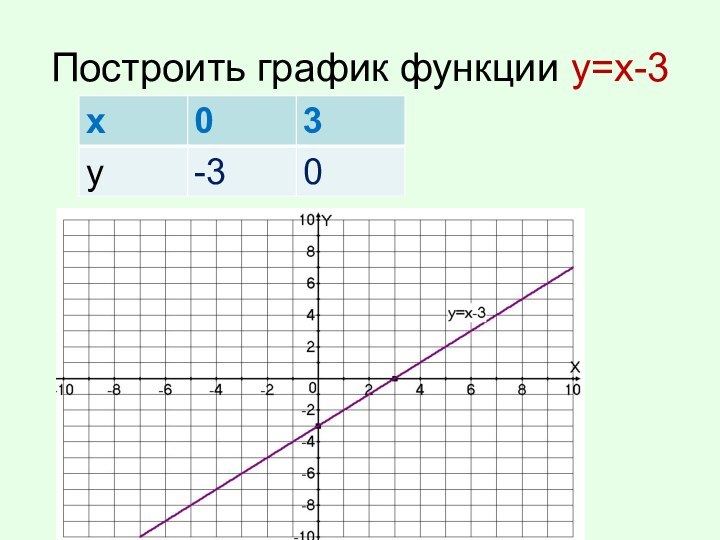
- 18. Построить график функции у=х-3
- 19. У=5
- 20. К =0
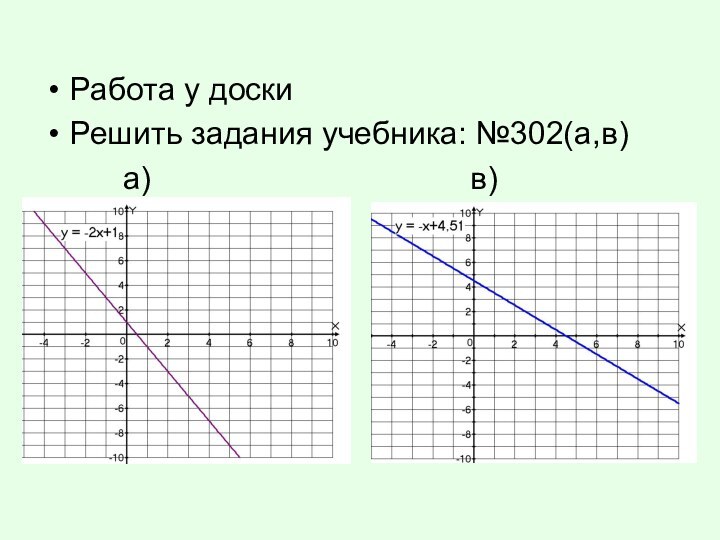
- 21. Работа у доскиРешить задания учебника: №302(а,в)
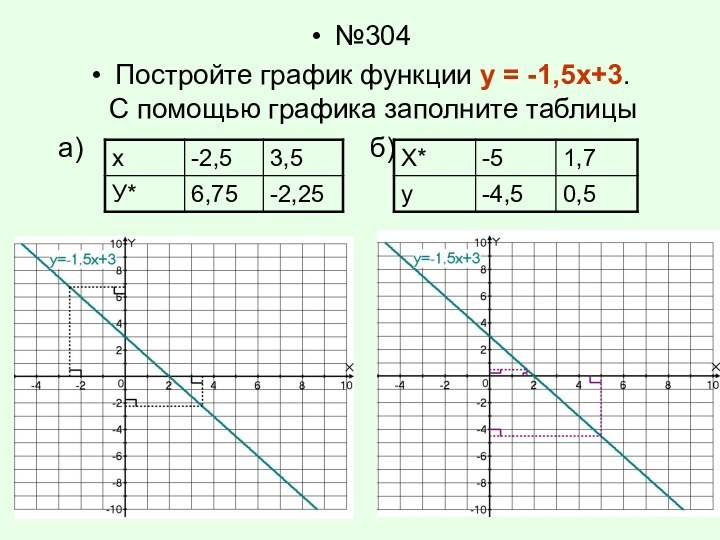
- 22. №304Постройте график функции у = -1,5х+3.
- 23. Групповая обучающая самостоятельная работа в четырёх вариантах.
- 24. Приложение 22 Алгоритм построения
- 26. Покажите схематическое изображение графика функции
- 28. 2.Что является графиком линейной функции? Графиком линейной функции является прямая линия.
- 29. Скачать презентацию
- 30. Похожие презентации
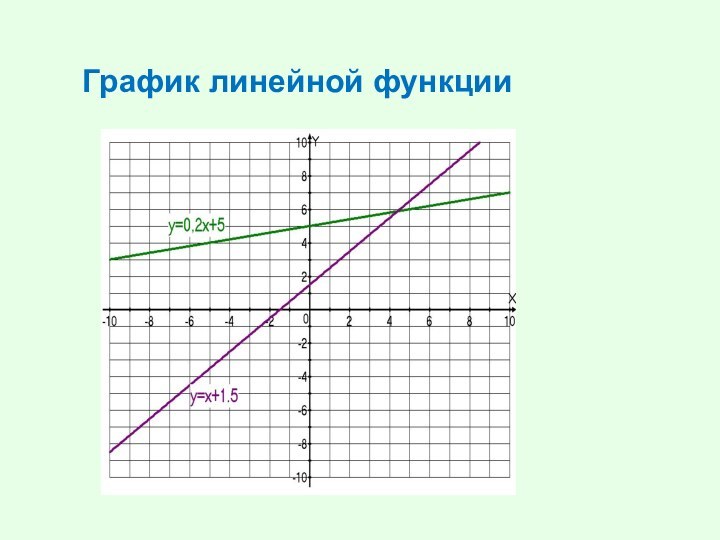
График линейной функции























Слайд 3
Цели урока:
Обучающие:
1. Учить строить график линейной функции;
2. Заполнять
по графику таблицу значений х и у;
график в зависимости от коэффициэнта k
Слайд 5
Развивающие:
Развитие логического мышления учащихся через использование ими специальных
методов обучения(анализ сравнение, обобщение, аналогия); математической речи; развитие внимания.
Слайд 6
План:
Актуализация знаний.
Изучение новой темы.
Закрепление: устные упражнения, задачи на
построение графиков.
Задание на дом. Подведение итога урока.
Слайд 7 1. В координатной плоскости отметьте точки: А(0;6), В(-3;4),
С(-4;0), М(2;-5), К(-4;-3).
2. Построить график функции
у = -2х+2.
Слайд 9
Составьте выражение к условию задачи:
На складе 500 тонн
угля. Ежедневно стали подвозить по 30 тонн. Сколько тонн
угля (у) будет на складе через 2, 4, х дней?У=500+30*2=560;
У=500+30*4=620;
У=500+30х
Слайд 10
Выполнить задание.
На складе было 500 тонн угля. Ежедневно
стали увозить по 30 тонн угля. Сколько тонн угля
(у) будет на складе через х дней?Проверьте:
У=500-30х
Вычислите значение у при х=2, х=5.
Слайд 11 Турист проехал на автобусе 15 километров от пункта
А до пункта В, а затем продолжил движение от
пункта В в том же направлении, но уже пешком со скоростью 4 км/час. На каком расстоянии (у) от пункта А будет турист через х часов ходьбы?Проверьте
У=15+4х
Вычислите значение у при х=2, при х=3.
Слайд 12
Что общего в полученных выражениях?
Сделайте вывод.
Определение линейной функции.
Линейной
функцией называется функция вида у = кх+b,
где к, b числа, х - независимая переменная (аргумент), у - зависимая переменная (функция).Записать в тетрадь определение.
Слайд 13
Какие из функций
1.
2.
3.
4.
5.
6.
7
являются линейными?
Проверьте: вторая, четвёртая,
пятая , шестаяНазовите аргумент, функцию.
Слайд 14 Найдите значение линейной функции у=2х-1 при заданном значении
аргумента х= 0, 2, 4, -1.
Заполните таблицу.
Отметьте
точки с данными координатами в системе координат.На какой линии лежат все эти точки? Сделайте вывод.
Слайд 16
Сколько точек нужно взять, чтобы построить прямую?
Для построения
прямой достаточно отметить две точки и провести через них
прямую линию.Слайд 23 Групповая обучающая самостоятельная работа в четырёх вариантах. №
302(б, г, д, е), при необходимости использовать алгоритм построения
графика функции и предписания для проверки правильности построения графика (приложение23 и приложение25 )№302(б, г) №302(д, е)
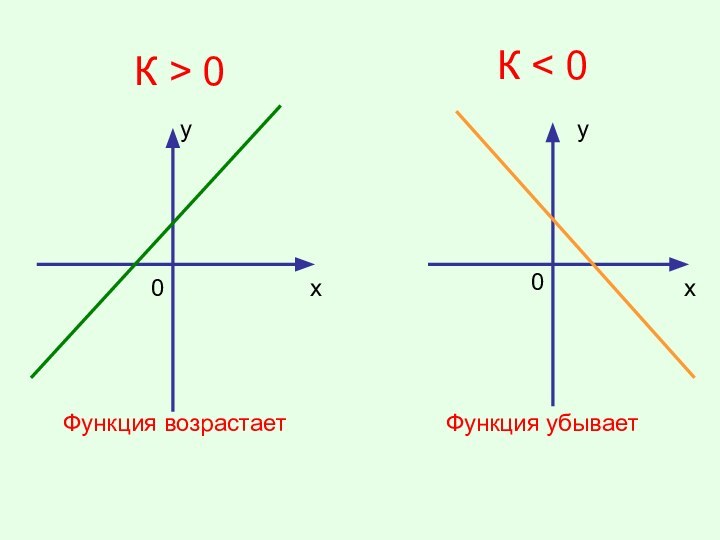
Сделайте вывод о схематическом расположении графика линейной функции при k>0 и k<0
Слайд 24
Приложение 22
Алгоритм построения графика
линейной функции.
Чтобы построить график линейной функции
нужно: 1. Задать два значения аргумента х;
2. Найти два соответствующих значения функции у;
3. Построить точки в системе координат;
4. Провести через них прямую линию.
Приложение25
Предписание для проверки правильности построения графика линейной функции
1. Возьми значение аргумента х, отличное от тех, которые использованы при построении графика;
2. Найди по формуле соответствующее значение функции у;
3. Построй точку с найденными координатами;
4. Проверь, принадлежит ли эта точка графику.
5. Если принадлежит, то график построен правильно, если нет – ищи ошибку.
Слайд 26 Покажите схематическое изображение графика функции у=2х-1,
у= -3х
№296 дополнительно
Проверьте y=120+0,5x
Домашнее задание: №303(а,б), №305, №297.Слайд 27
Итог урока:
1. Какая функция называется
линейной?Линейной функцией называется функция вида
у = кх+b,
где к, b числа, х - независимая переменная (аргумент), у - зависимая переменная (функция).