= a
Определение арккосинуса
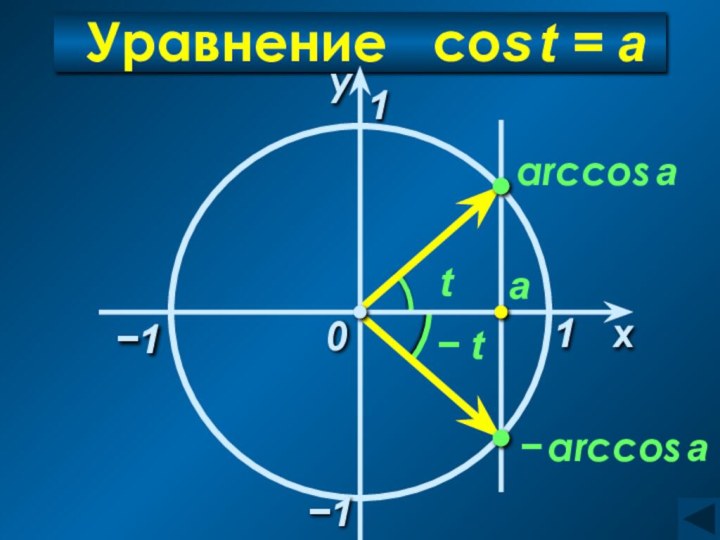
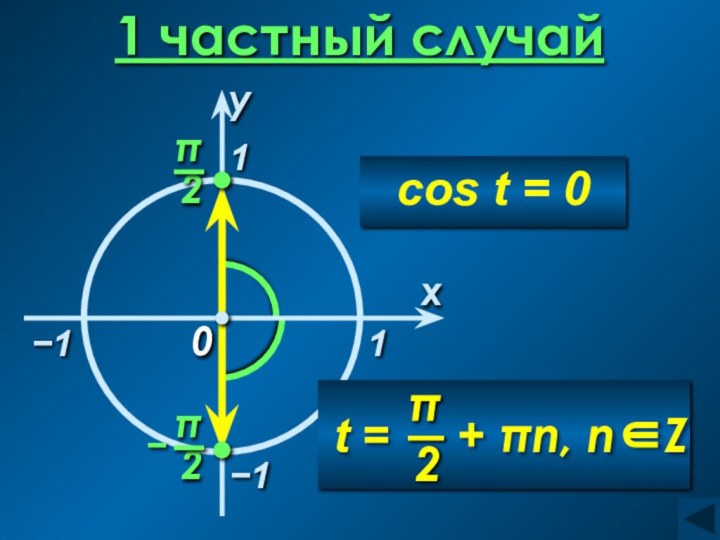
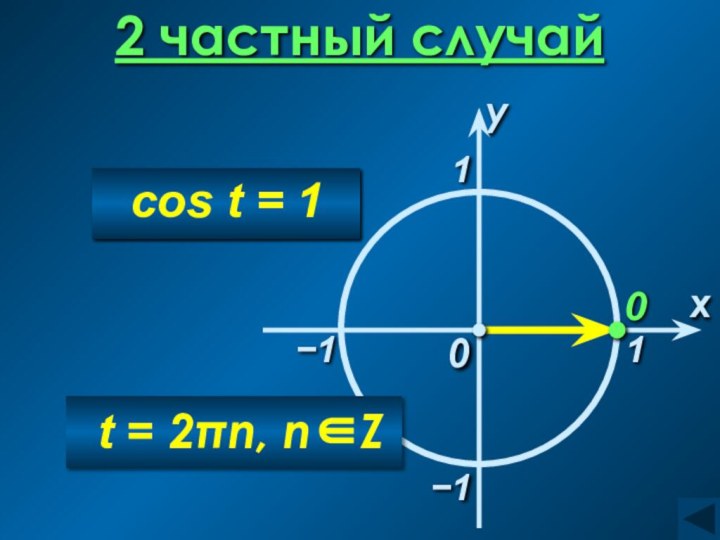
Уравнение cos t = a
Определение арктангенсаУравнение tg t = a
Определение арккотангенса
Уравнение ctg t = a
Примеры
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



![Решение тригонометрических уравнений и неравенств Определение арксинусаАрксинусом числа а называется такой угол из промежутка [− 0,5π; 0,5π],](/img/tmb/6/562337/6b0e0ec46ba97d86bce77a4102e7babb-720x.jpg)


![Решение тригонометрических уравнений и неравенств Определение арккосинусаАрккосинусом числа а называется такой угол из промежутка [ 0; π],](/img/tmb/6/562337/7f65887cfbfb008df1ee6cf4fe745f20-720x.jpg)























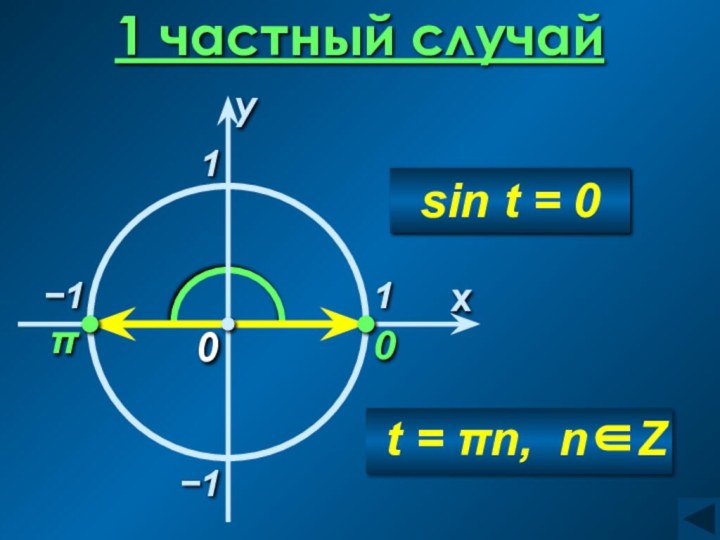
arcsin a = t , sin t = a
где t ∈ [− 0,5π; 0,5π]
а ∈ [− 1; 1]
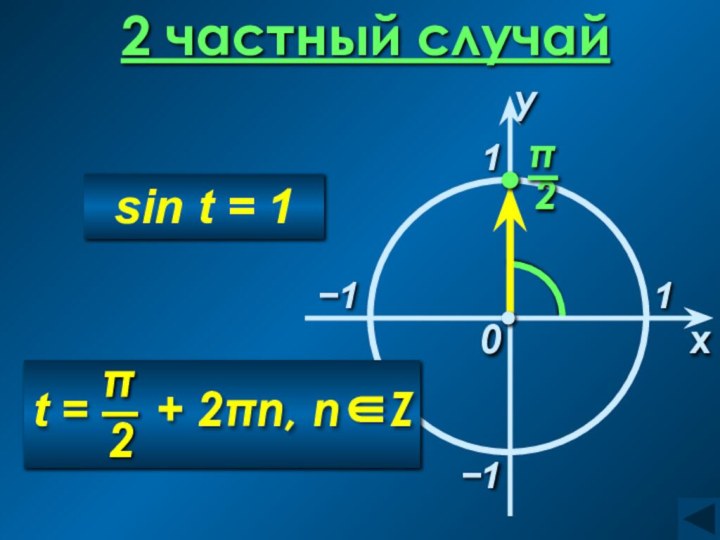
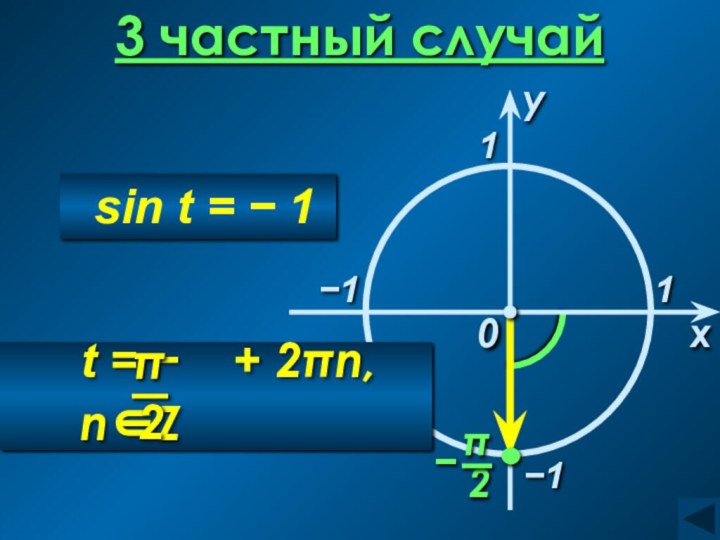
sin(arcsin a) = a, а ∈ [− 1; 1]
arcsin(sin t) = t, t ∈ [− 0,5π; 0,5π]
Пример
arccos a = t , cos t = a
где t ∈ [ 0; π]
а ∈ [− 1; 1]
cos(arccos a) = a, a ∈ [-1; 1]
arccos(cos t) = t, t ∈ [ 0; π]
tg(arctg a) = a
arctg(tg t) = t, t ∈ (− 0,5π; 0,5π)
arctg (−a) = − arctg a
сtg(arсctg a) = a
arcсtg(сtg t) = t, t ∈ (0; π)
arсctg (−a) = π − arcсtg a
π
-π
2
3
-1
-2
-3
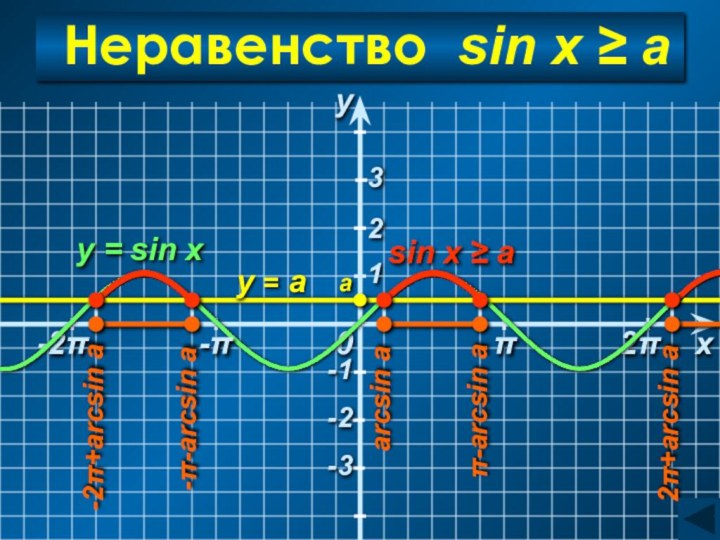
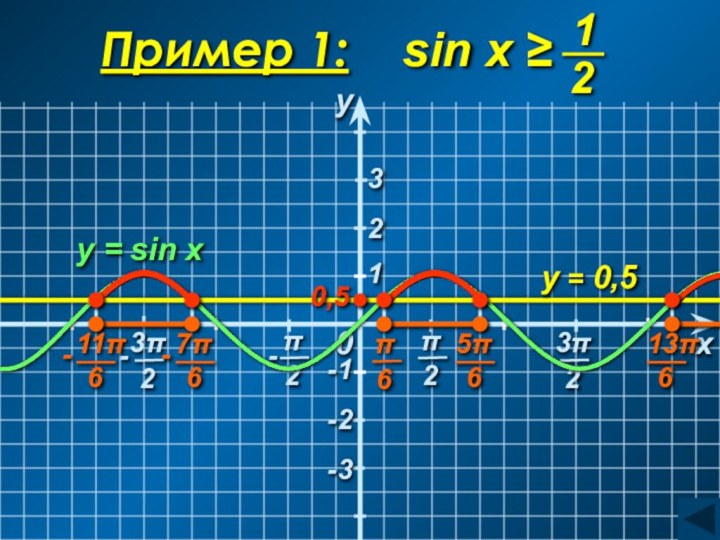
arcsin a ≤ x ≤ π − arcsin a
C учетом периодичности:
Ответ:
[arcsin a + 2πn; π − arcsin a + 2πn], n∈Z
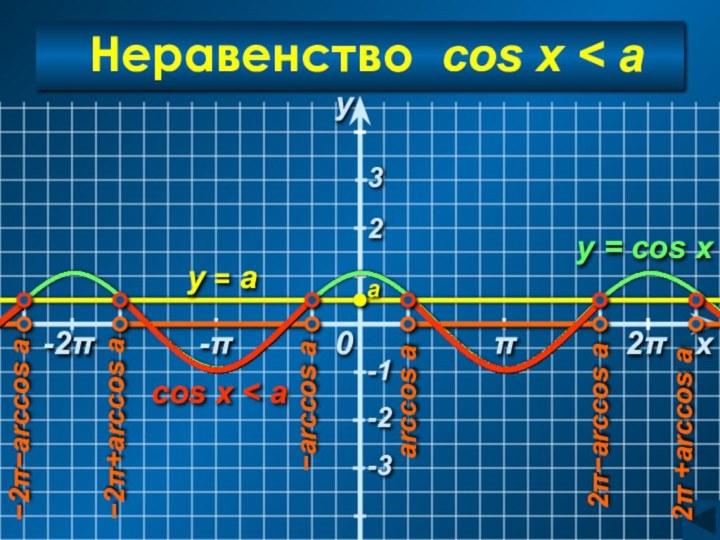
cos x < a
π
-π
2π
-2π
2
3
-1
-2
-3
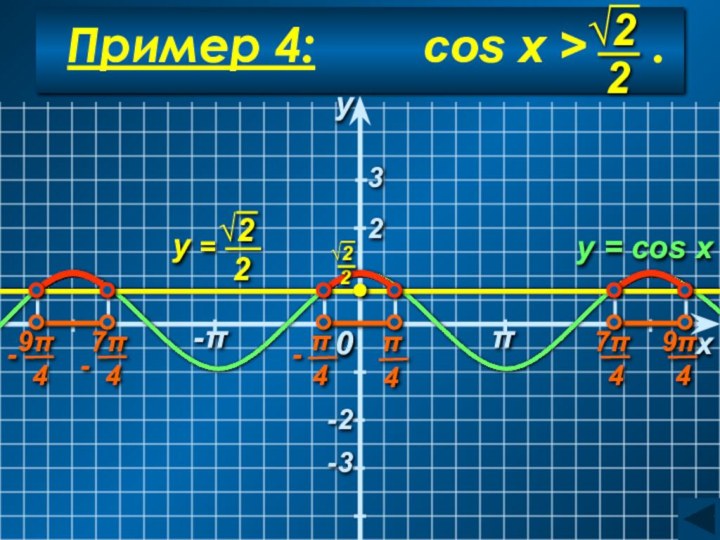
arccos a < x < 2π − arccos a
C учетом периодичности:
Ответ:
(arccos a + 2πn; 2π − arccos a + 2πn), n∈Z
4
3
-2π
-π
π
2π
0
-3
-4
-2
1
2
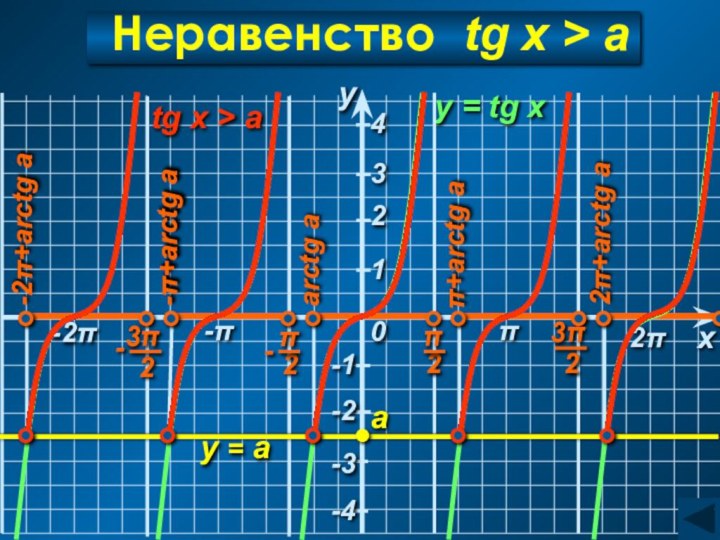
[arctg a + πn; π+ πn), n∈Z