- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Введение в теорию множеств. Действия над множествами
Содержание
- 2. Урок № 72§11. Неравенства с одной переменной
- 3. Множество – это совокупность объектов, объединенных между собой по какому-либо признаку:
- 4. Множество есть многое, мыслимое, как единоеГеорг Кантор
- 6. 1. Непосредственным перечислением всех его элементов.Указанием характеристического
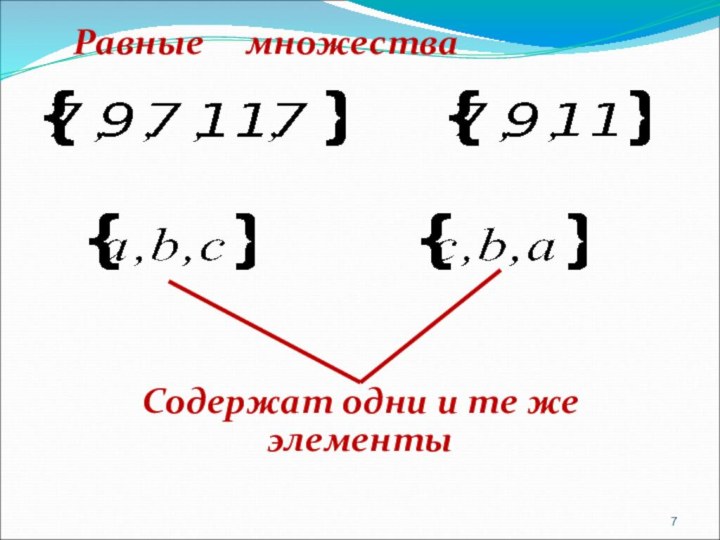
- 7. Равные множестваСодержат одни и те же элементы
- 8. Действия над множествамиПересечением множеств – называется множество, состоящее из всех общих элементов этих множеств
- 9. Действия над множествами. Круги Эйлера1234567
- 10. Действия над множествамиОбъединением множеств – называется множество,
- 11. Действия над множествами. Круги Эйлера1234567
- 12. Назовите известные вам множества людейЗапишите множества, элементами которых являются:Планеты Солнечной системы;Столицы государств;Числа, кратные 7;Делители числа 36.
- 13. Верна ли запись?
- 14. Даны множества?Найдите:
- 15. Кл/р № 799,№ 801(а),№ 802(а),№ 803,№ 804(а),№ 806.Д/З п.29№ 800,№ 801(б),№ 802(б),№ 804(б).
- 16. Скачать презентацию
- 17. Похожие презентации
Урок № 72§11. Неравенства с одной переменной и их системы Основные понятия теории множеств. Пересечение и объединение множеств















Слайд 6
1. Непосредственным перечислением всех его элементов.
Указанием характеристического свойства,
т.е. такого свойства, которым обладают все элементы этого множества
и не обладает предмет, не являющийся его элементом.Способы задания множеств