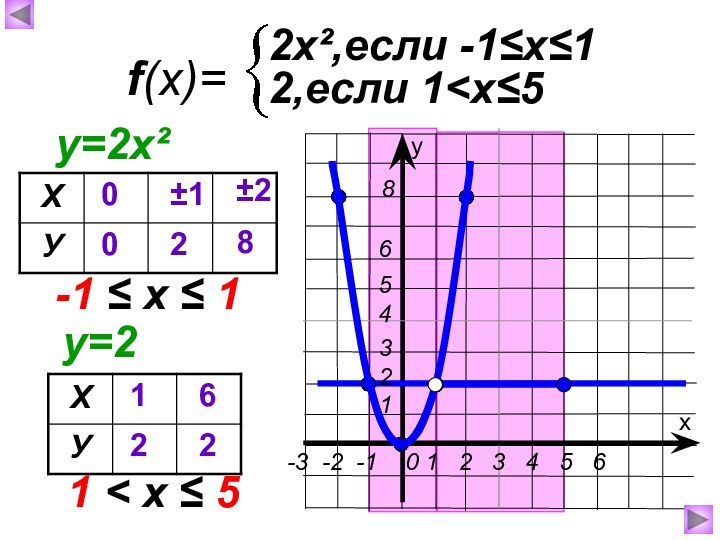
0
-3 -2 -11
9
4
Ось симметрии
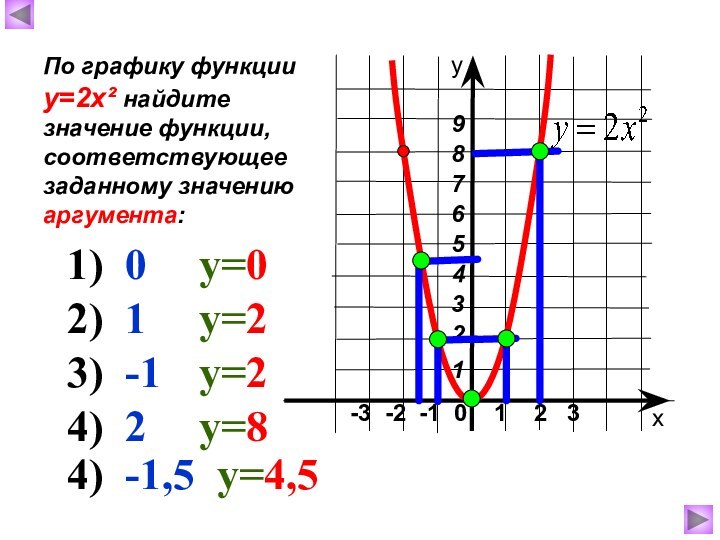
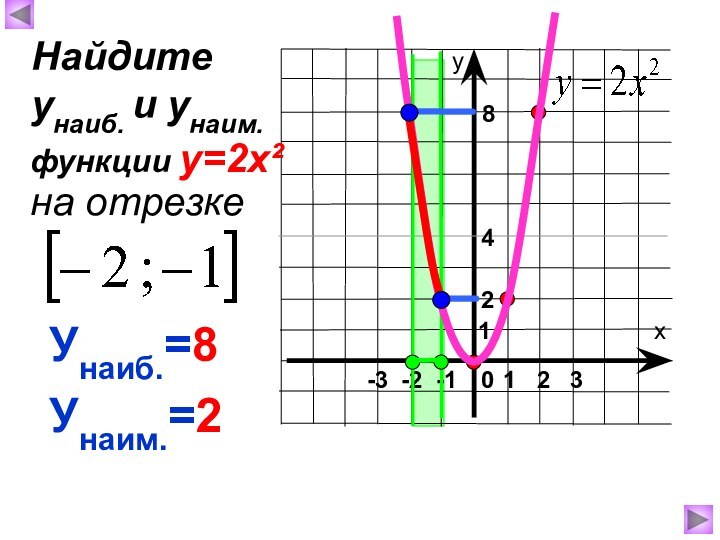
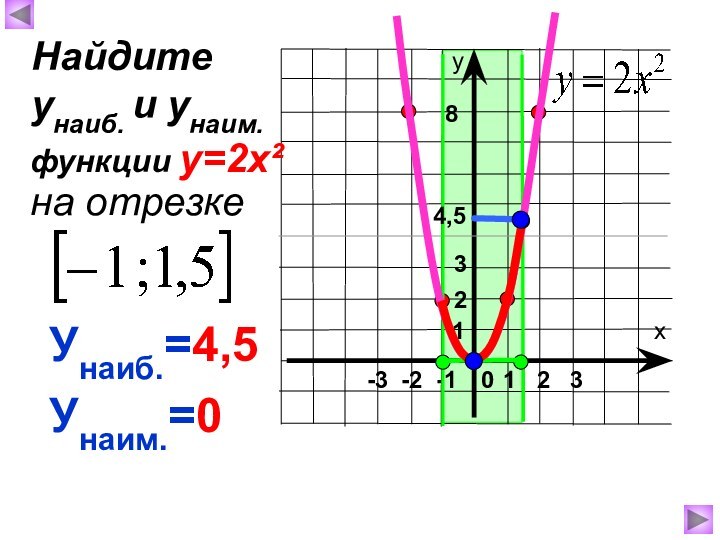
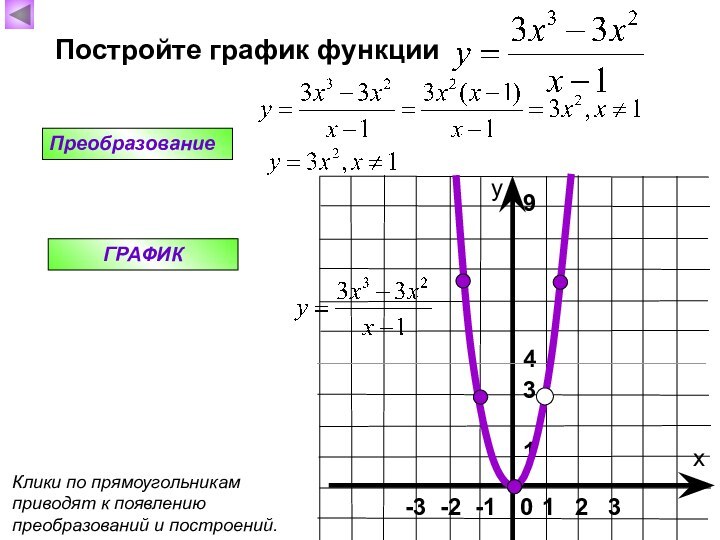
Графиком является парабола.
Вершина параболы
Ветвь параболы
Ветвь параболы
Ветви направлены вверх
Точка (0;0) – вершина параболы
Ось у- ось симметрии
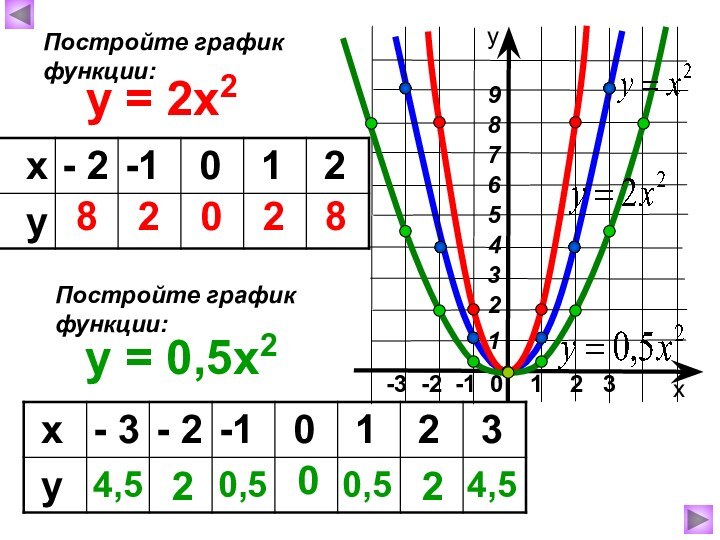
Построим график функции у=х² для этого значения аргумента (х) выберем сами, а значения функции (у) вычислим по формуле у=х².