в живописи и поэзии».
Н.Е.Жуковский
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку-конференции Применение формул сокращенного умножения 7 класс
Содержание
- 2. «В математике есть своя красота,
- 3. Альбрехт Дюрер. Автопортрет.
- 4. Альбрехт Дюрер. Дева Мария с младенцем и святой Анной
- 5. Альбрехт Дюрер. Лев
- 6. Альбрехт Дюрер. Долина Калькройт
- 7. Формулы сокращенного умноженияквадрат суммыквадрат разностиразность квадратовразность кубовсумма
- 8. (102+112+122)+(132+142)365
- 9. Известный способ: (102+112+122) + (132+142) = 365=
- 10. А с помощью формул сокращённого умножения
- 11. Упростить выражение. (2+1)(22+1)(24+1)(28+1)(216+1)(232+1)Колб Екатерина Это очень легко сделать, если знаешь маленькую хитрость!(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)==(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)==(22-1)(22+1)(24+1)(28+1)(216+1)(232+1)==(24-1)(24+1)(28+1)(216+1)(232+1)==(28-1)(28+1)(216+1)(232+1)==(216-1)(216+1)(232+1)=(232-1)(232+1)==264-1
- 12. Хотите, докажу!Р2-1 делится на 24, если Р – простое число, большее 3Всегда?!
- 13. Р2-1=(Р-1)(Р+1)24=23*3=8*3
- 14. Р-1, Р, Р+1-последовательные числаР-1 и Р+1-чётные последовательные
- 15. Доказательство проводила Колб ЕкатеринаПравда просто?
- 16. Есть числа с очень удивительными свойствами. Например,
- 17. Как определить остальные средние цифры чисел с
- 18. 1122=(100+10+2)2=1002+102+22+2*100*10+2*100*2+2*10*2==10000+100+4+2000+4000+40=125442112=(200+10+1)2=2002+102+12+2*200*10+2*200*1+2*10*1==40000+100+1+4000+400+20= 44521(a + b+c)2 = a2+b2+c2+2ab+2ac+2bc(a +
- 19. ПРЕЗЕНТАЦИЯ
- 20. ВАМ СЛАБО РЕШИТЬ ТАКОЕ УРАВНЕНИЕ??? х8+х4-2=0
- 21. Мне НЕТ И Я С УДОВОЛЬСТВИЕМ
- 22. Чтобы решить это коварное уравнение нам понадобится:1)
- 24. Ответ: -1 и 1
- 26. В уравнении количество корней равно
- 27. Создатель презентацииМакаёва Юлия 7а
- 28. (102+112+122)+(132+142)365
- 29. Найти пять последовательных натуральных чисел таких, что
- 30. откуда взялось название «формулы квадрата суммы», «разности квадратов»? А вы знаете,
- 31. a2b2abab(a+b)2=(a+b)2=a2+b2+2abА ВОТ ОТКУДА!Если сторона квадрата равна сумме a+b, то его площадь
- 32. a2-b2=a(a-b)+b(a-b)=(a-b)(a+b)РАЗНОСТЬ КВАДРАТОВВозьмем квадрат со стороной аИ отрежем от него квадрат со стороной bПлощадь оставшейся фигуры
- 33. Формулы кубов тоже не зря так назвали!
- 34. b3bbaabaa3
- 35. ++a3b3
- 36. +aaaaaabbb++
- 37. +++aaabbbbbb
- 38. (a+b)3=a3+b3+3a2b+3ab2В итоге получаем:
- 39. теорема ПифагораSa+b=2ab+а2+b2 аbbааccccc2bbааbcа2b2аbbааbSa+b=4• ab+c2 =2ab+ c2 2ab + c22ab +а2+b2c2=а2+b2
- 41. Задача о лотосеНад озером тихим, с полфута
- 43. Составим уравнение
- 44. Как бы машина хорошо
- 45. Скачать презентацию
- 46. Похожие презентации
«В математике есть своя красота, как в живописи и поэзии». Н.Е.Жуковский
Слайд 7
Формулы сокращенного умножения
квадрат суммы
квадрат разности
разность квадратов
разность кубов
сумма кубов
куб
суммы
куб разности
(а + b)2 = a2
+ b2 + 2ab (а - b)2 = a2 + b2 - 2ab
а2 - b2 = (a – b)(a + b)
а3 – b3=(a – b) (a2+ ab + b2 )
а3 + b3 =(a + b) (a2- ab + b2)
(а + b)3 = a3 + 3a2b + 3ab2 + b3
(а - b)3 = a3 – 3a2b + 3ab2 - b3
Слайд 9
Известный способ:
(102+112+122) + (132+142) =
365
= (100+121+144)
+ (169+196) =
365
= 365
+ 365 =2365
Слайд 10 А с помощью формул сокращённого умножения
можно выполнить вычисления и так:
102 + (10+1)2 + (10+2)2 +(10+3)2 + (10+4)2= =102+102+1+20+102+4+40+102+9+60+
+102+16+80=500+200+30=730
730:365 = 2
Тоже очень просто, согласитесь!
Слайд 11
Упростить выражение. (2+1)(22+1)(24+1)(28+1)(216+1)(232+1)
Колб
Екатерина
Это очень
легко сделать, если знаешь маленькую хитрость!
(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)=
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)=
=(22-1)(22+1)(24+1)(28+1)(216+1)(232+1)=
=(24-1)(24+1)(28+1)(216+1)(232+1)=
=(28-1)(28+1)(216+1)(232+1)=
=(216-1)(216+1)(232+1)=(232-1)(232+1)=
=264-1
Слайд 14
Р-1, Р, Р+1-последовательные числа
Р-1 и Р+1-чётные последовательные числа,
одно из которых делится на 2,
а второе на
4, т.е. (Р-1)(Р+1) делится на 8.
Одно из трёх последовательных чисел всегда делится на 3, это не Р,
значит Р-1 или Р+1 делится на 3
и Р2-1 делится на 3.
Если Р2-1 делится на 8 и на 3, значит делится и на 24.
Слайд 16
Есть числа с очень удивительными свойствами. Например, число
- 12 ,наоборот - 21,
122=144 ⇨
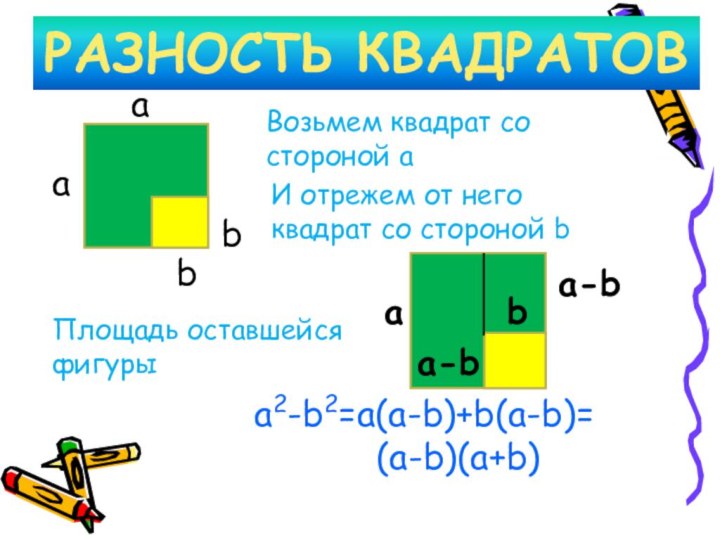
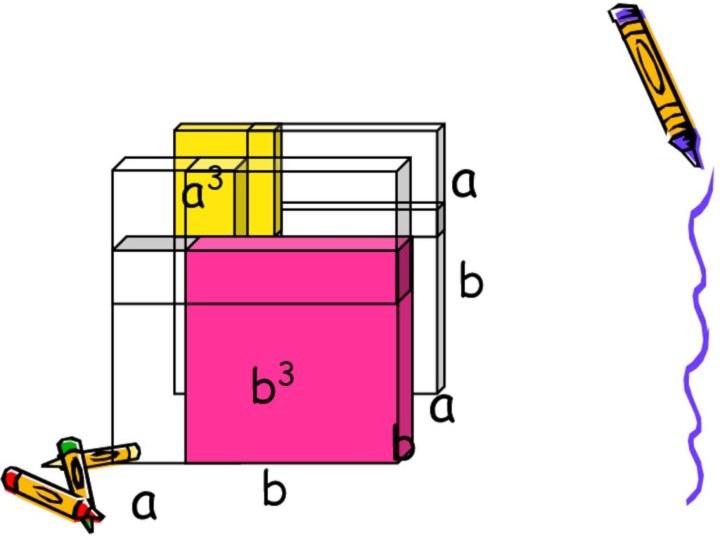
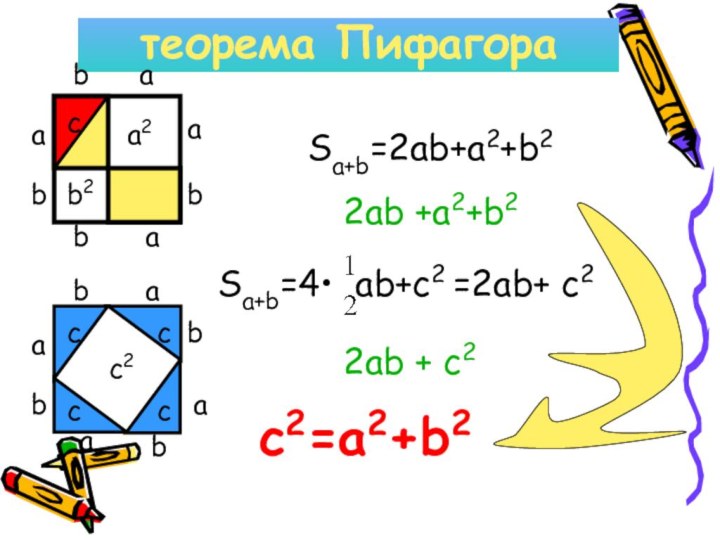
212=441Квадрат окажется тоже цифрами записанными теми же числами в обратном порядке.
122= (10+2)2=100+4+40=144
212=(20+1)2=400+1+40=441
132=(10+3)2=100+9+60=169
312=(30+1)2=900+1+60=961
Я думаю, что у всех чисел с таким свойством первая и последняя цифра не больше 3, т.к.
12=1
22=4 однозначные числа
32=9
Слайд 17
Как определить остальные средние цифры чисел с таким
свойством?
Наверное, это числа из " 1,2,3" или
начинающихся на 11, 12, 13 или заканчивающимся этими числами.
И опытным путём я нашла числа с такими свойствами.
102 и 201
112 и 211
122 и 221
133 и 331
...
Напр. 1022=10404
2012=40401
Добродей
Юлия
Остальные числа, если вас заинтересовало - проверьте сами.
Слайд 18
1122=(100+10+2)2=1002+102+22+2*100*10+2*100*2+2*10*2=
=10000+100+4+2000+4000+40=12544
2112=(200+10+1)2=2002+102+12+2*200*10+2*200*1+2*10*1=
=40000+100+1+4000+400+20= 44521
(a + b+c)2 = a2+b2+c2+2ab+2ac+2bc
(a + b
- c)2=a2+b2+c2+2ab-2ac-2bc
(a - b - c)2=a2+b2+c2-2ab-2ac+2bc
Зная, эти формулы легко
возвести в квадрат трехзначное числоКовалец Анастасия
Слайд 22
Чтобы решить это коварное уравнение нам понадобится:
1) знание
формул сокращённого умножения
2) немного терпения
3) и конечно же умственное
напряжениеСлайд 26 В уравнении количество корней равно или
меньше его степени!!!
Поэтому нам и пришлось решать,
чтобы убедиться, что других корней в уравнении нет.
Слайд 29
Найти пять последовательных натуральных чисел таких, что сумма
квадратов двух больших из них
равна сумме квадратов трёх
остальных.n2-6n+5=6n+5,
n2-12n=0,
n(n-12)=0,
n=0 или n=12,
0 – не является натуральным числом.
Ответ:10; 11; 12; 13; 14.
Других чисел с этим свойством нет.
Лозицкая
Дарья
Пусть n-2, n-1, n, n+1 и n+2 пять последовательных чисел,
(n-2)2; (n-1)2; n2; (n+1)2; (n+2)2
По условию задач должно выполняться равенство:
(n+1)2+(n+2)2=(n-2)2+(n-1)2+n2,
n2+2n+1+n2+4n+4=n2-4n+4+n2-2n+1+n2,
Слайд 31
a2
b2
ab
ab
(a+b)2=
(a+b)2=a2+b2+2ab
А ВОТ ОТКУДА!
Если сторона квадрата равна сумме a+b,
то его площадь
Слайд 32
a2-b2=a(a-b)+b(a-b)=
(a-b)(a+b)
РАЗНОСТЬ КВАДРАТОВ
Возьмем квадрат со стороной а
И отрежем от
него квадрат со стороной b
Площадь оставшейся фигуры
Слайд 39
теорема Пифагора
Sa+b=2ab+а2+b2
а
b
b
а
а
c
c
c
c
c2
b
b
а
а
b
c
а2
b2
а
b
b
а
а
b
Sa+b=4• ab+c2 =2ab+ c2
2ab + c2
2ab +а2+b2
c2=а2+b2
Слайд 41
Задача о лотосе
Над озером тихим, с полфута размером,
Высился
лотоса цвет,
Он рос одиноко. И ветер порывом
Отнёс его в
сторону. НетБолее цветка над водой.
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Слайд 44 Как бы машина хорошо не
работала, она может решать все требуемые от нее задачи,
но она никогда не придумает ни одной.Альберт Эйнштейн
