- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема об отрезках пересекающихся хорд
Содержание
- 2. «Теорема об отрезках пересекающихся хорд »Цель
- 3. Домашнее задание (проверка)!!!
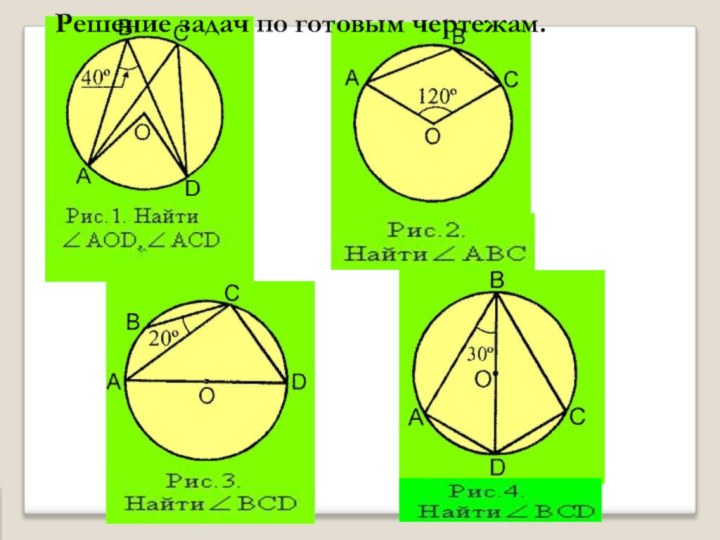
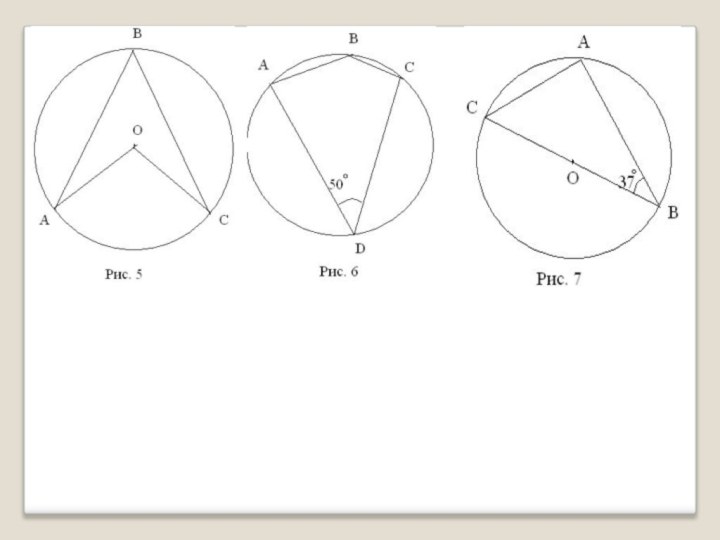
- 4. Решение задач по готовым чертежам.
- 6. Теорема Если две хорды окружности пересекаются, то
- 7. Хорды окружности РТ и КМ пересекаются в
- 8. Работа с учебником№ 667№ 670_____№ 666 (а)№ 671 (а)
- 9. Итоги урокаОтветьте на вопросы:- Что нового я
- 10. Скачать презентацию
- 11. Похожие презентации
«Теорема об отрезках пересекающихся хорд »Цель урока: Изучить теорему о произведении пересекающихся хорд, и показать ее применение при решении задач.







Слайд 6
Теорема
Если две хорды окружности пересекаются, то произведение
отрезков
одной хорды равно произведению отрезков другой хорды.
Доказательство:
Пусть
хорды AB и CD пересекаются в точке EДокажем, что АЕ • ВЕ = СЕ • DЕ
Рассмотрим ∆ АDE и ∆ CBE.
В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются
на одну и ту же дугу.
Углы 3 и 4 равны как вертикальные.
По первому признаку подобия треугольников ∆ ADE~ ∆ CBE.
Отсюда следует, что АЕ:СЕ = DЕ:ВЕ, или АЕ • ВЕ = СЕ • DЕ
Что и требовалось доказать.
Слайд 7
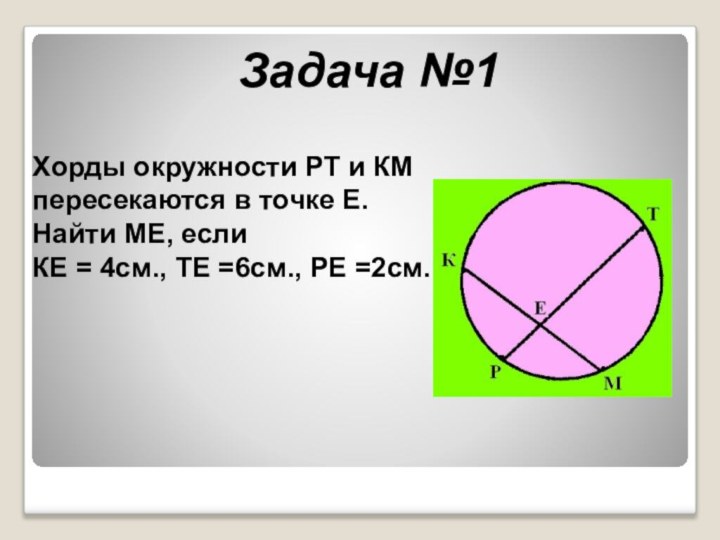
Хорды окружности РТ и КМ пересекаются в точке
Е. Найти МЕ, если
КE = 4cм., ТE =6см.,
РE =2см.Задача №1





























