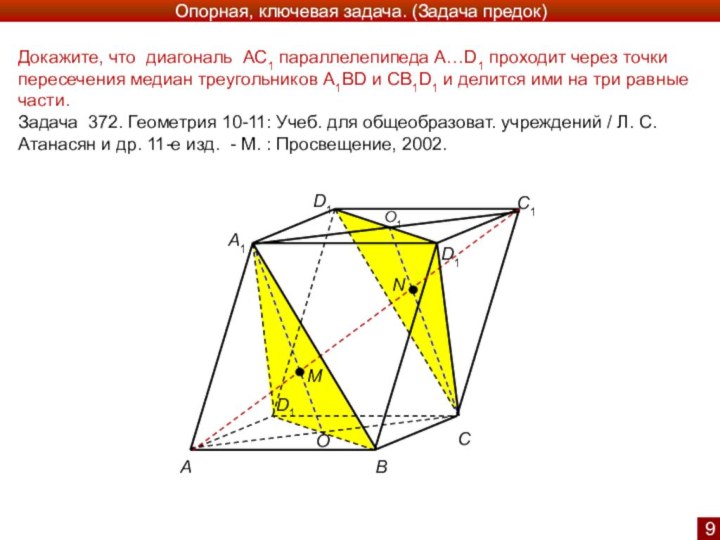
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Угол между прямой и плоскостью. Подготовка к ЕГЭ (10-11 класс)
Содержание
- 2. Рисунок неудачный:плоскость треугольника CB1D1 плохо просматриваетсяПоменяли местами буквы A и A1. Теперь все хорошо просматривается.2
- 3. C1B1CBDD1Так как АВ║С1D1, то угол между прямой
- 4. Так как АВ║С1D1, то угол между прямой
- 5. Так как АВ║С1D1, то угол между прямой
- 6. Прямые АС1 и СО1 лежат в
- 7. Таким образом, С1М – перпендикуляр к плоскости
- 8. C1B1CBDD1О1MCC1A1AО1Треугольники С1МО1 и АМС подобны по двум
- 9. Скачать презентацию
- 10. Похожие презентации






Слайд 2
Рисунок неудачный:
плоскость треугольника CB1D1 плохо просматривается
Поменяли местами буквы
A и A1. Теперь все хорошо просматривается.
Слайд 3
C1
B1
C
B
D
D1
Так как АВ║С1D1, то угол между прямой АВ
и пл. CB1D1 равен углу между прямой C1D1 и
пл. CB1D1.3
A1
A
Слайд 4 Так как АВ║С1D1, то угол между прямой АВ
и пл. CB1D1 равен углу между прямой C1D1 и
пл. CB1D1.C1
B1
A1
C
B
A
D
D1
A1C1 является проекцией наклонной АС1 на пл. A1B1C1D1
По теореме о трех перпендикулярах
B1D1 ┴ АС1
(прямая B1D1 лежит в плоскости A1B1C1D1 и перпендикулярна к проекции A1C1 наклонной АС1 на плоскость A1B1C1D1 поэтому она (B1D1) перпендикулярна и к самой наклонной АС1 )
4
Слайд 5 Так как АВ║С1D1, то угол между прямой АВ
и пл. CB1D1 равен углу между прямой C1D1 и
пл. CB1D1.C1
B1
A1
C
B
A
D
D1
A1C1 является проекцией наклонной АС1 на пл. A1B1C1D1
По теореме о трех перпендикулярах
B1D1 ┴ АС1
(прямая B1D1 лежит в плоскости A1B1C1D1 и перпендикулярна к проекции A1C1 наклонной АС1 на плоскость A1B1C1D1 поэтому она (B1D1) перпендикулярна и к самой наклонной АС1 )
Аналогично СB1 ┴ АС1
(прямая СB1 лежит в плоскости СС1B1B и перпендикулярна к проекции BC1 наклонной АС1 на плоскость СС1B1B поэтому она (CB1) перпендикулярна и к самой наклонной АС1 )
5
Слайд 6 Прямые АС1 и СО1 лежат в одной
плоскости АА1С1С и пересекаются в некоторой точке М, которая
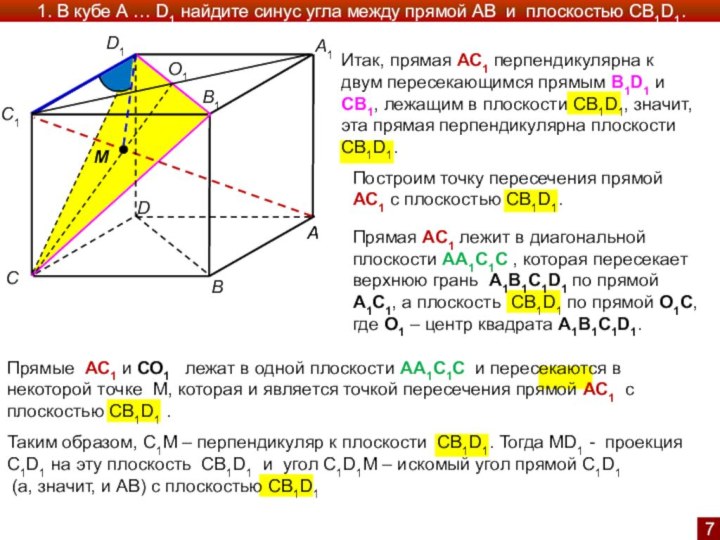
и является точкой пересечения прямой АС1 с плоскостью СB1D1 .Прямая АС1 лежит в диагональной плоскости АА1С1С , которая пересекает верхнюю грань A1B1C1D1 по прямой А1С1, а плоскость СB1D1 по прямой О1С, где О1 – центр квадрата A1B1C1D1.
Построим точку пересечения прямой АС1 с плоскостью CB1D1.
C1
B1
C
B
D
D1
О1
M
6
A1
A
Итак, прямая АС1 перпендикулярна к двум пересекающимся прямым B1D1 и CB1, лежащим в плоскости CB1D1, значит, эта прямая перпендикулярна плоскости СB1D1.
Слайд 7 Таким образом, С1М – перпендикуляр к плоскости СB1D1.
Тогда MD1 - проекция С1D1 на эту плоскость СB1D1
и угол С1D1M – искомый угол прямой C1D1(а, значит, и АВ) с плоскостью СB1D1
C1
B1
C
B
D
D1
О1
M
7
A
Прямая АС1 лежит в диагональной плоскости АА1С1С , которая пересекает верхнюю грань A1B1C1D1 по прямой А1С1, а плоскость СB1D1 по прямой О1С, где О1 – центр квадрата A1B1C1D1.
Построим точку пересечения прямой АС1 с плоскостью CB1D1.
A1
A
Итак, прямая АС1 перпендикулярна к двум пересекающимся прямым B1D1 и CB1, лежащим в плоскости CB1D1, значит, эта прямая перпендикулярна плоскости СB1D1.
Прямые АС1 и СО1 лежат в одной плоскости АА1С1С и пересекаются в некоторой точке М, которая и является точкой пересечения прямой АС1 с плоскостью СB1D1 .
Слайд 8
C1
B1
C
B
D
D1
О1
M
C
C1
A1
A
О1
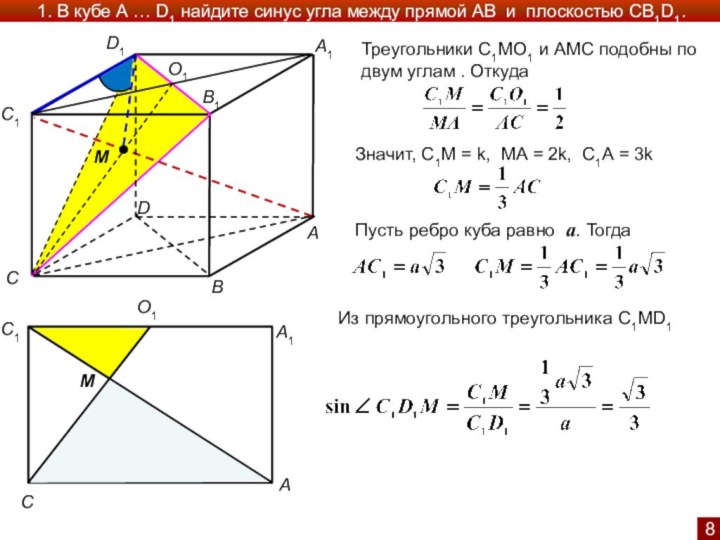
Треугольники С1МО1 и АМС подобны по двум углам
. Откуда
M
Пусть ребро куба равно а. Тогда
Значит, С1М
= k, МА = 2k, С1А = 3k Из прямоугольного треугольника C1MD1
8
A1
A





























