Слайд 2
1. Расположите в порядке убывания числа: 0,1327; 0,014;
0,13
А) 0,1327; 0,014; 0,13
Б) 0,014; 0,13; 0,1327
В) 0,1327; 0,13;
0,014
Г) 0,13; 0,014; 0,1327
2. При каком из указанных значений х выражение
не имеет смысла?
А) при х = -2
Б) при х = -1
В) при х = 1
Г) при х = 0
Слайд 3
Числовые
последовательности
Слайд 4
Определение. Функцию y = f(x), x€N,
называют функцией
натурального аргумента или числовой последовательностью
и обозначают y =
f(n) или y1, y2, y3,…,yn,…
y1 – первый член последовательности,
y2 - второй член последовательности,
y3 - третий член последовательности,
yn - n-ый член последовательности,
n - индекс, который задает порядковый номер
Определение числовой последовательности
Слайд 5
Обозначение членов последовательности
1, 2, 3, 4, 5, …,
n-1, n, n+1,…
a1, a2, a3, a4, a5, …, an-1,
an, an+1,…
Слайд 6
Последовательностью называется
бесконечное
множество пронумерованных элементов.
Слайд 7
Дни
недели
Названия
месяцев
Классы
в школе
Номер
счёта
в банке
Дома
на улице
Последовательности составляют
такие элементы природы,
которые можно пронумеровать
Слайд 8
Способы задания последовательностей
Аналитический –
с помощью формулы n-ого
члена – позволяет вычислить член последовательности с любым заданным
номером
хn=3×n+2
x5=3 ×5+2=17;
Х45=3×45+2=137
Рекуррентный
(от слова recursio - возвращаться)
х1=1; хn+1=(n+1); xn
n=1; 2; 3; …
можно записать с многоточием
1; 2; 6; 24; 120; 720; …
Словесный
Слайд 9
Рассмотрим функцию
График состоит из отдельных точек.
…
Слайд 10
Последовательность квадратов натуральных чисел
Слайд 11
Способы задания последовательности
Аналитическое задание числовой
последовательности.
Пример 1:
yn=n2
последовательность 1,4,9,16,…, n2,…
Слайд 12
Способы задания последовательности
Аналитическое задание числовой
последовательности.
Слайд 13
Способы задания последовательности
Аналитическое задание числовой
последовательности.
Пример 3:
Задать последовательность формулой n-го
члена:
а) 2, 4, 6, 8, … б) 4, 8, 12, 16, 20, …
Слайд 14
1) Что называют числовой последовательностью?
2) Как ее
можно задать?
3) Какой способ помогает быстрее отыскать любой член
последовательности?
Сегодня на уроке
Я запомнил…
Я узнал…
Я научился…
В дальнейшем мне хотелось бы…
Рефлексия
Слайд 15
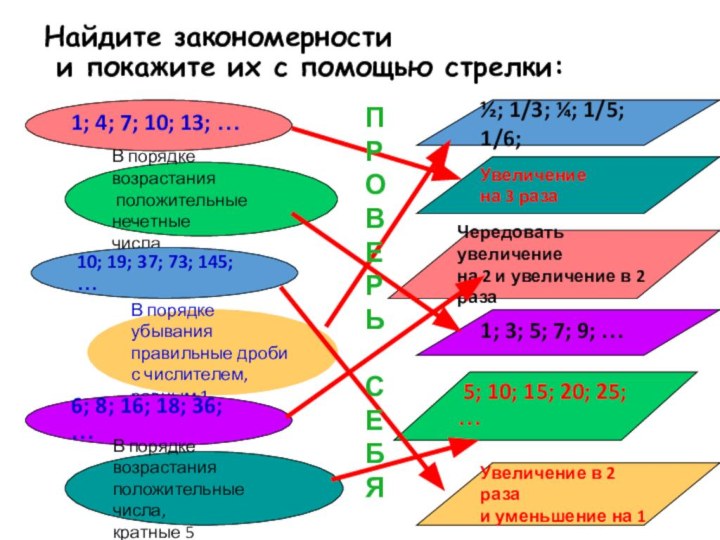
Найдите закономерности
и покажите их с помощью стрелки:
1;
4; 7; 10; 13; …
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3 раза
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
П
Р
О
В
Е
Р
Ь
С
Е
Б
Я
Слайд 16
Способы задания последовательности
Словесное задание числовой
последовательности.
Правило составления последовательности описывается словами
Пример :
последовательность простых чисел
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
последовательность кубов натуральных чисел
1, 8, 27, 64, 125, …
Слайд 17
Способы задания последовательности
Рекуррентное задание числовой
последовательности.
Указывается правило позволяющее вычислить n-й член последовательности, если известны
ее предыдущие члены.
При вычислении членов последовательности по этому правилу мы все время возвращаемся назад, выясняем чему равны предыдущие члены, поэтому такой способ называют рекуррентным ( от латинского recurrere – возвращаться)
Слайд 18
Способы задания последовательности
Рекуррентное задание числовой
последовательности.
Пример 1:
y1=3, yn= yn-1 + 4, если n =
2, 3, 4, …
Каждый член последовательности получается из предыдущего прибавлением к нему числа 4
y1 = 3 y2 = y1 + 4= 3 + 4 = 7
y3= y2+ 4= 7 + 4 = 11 y4 = y3 + 4= 11 + 4 = 15 и т.д.
Получаем последовательность
3, 7, 11, 15, 19, 23, 27, …
Слайд 19
Способы задания последовательности
Рекуррентное задание числовой
последовательности.
Пример 2:
y1=1, y2=1, yn= yn-2 + yn-1
Каждый член последовательности
равен сумме двух предыдущих членов
y1=1 y2=1 y3= y1 + y2 = 1 + 1 = 2
y4 = y2 + y3= 1 + 2 = 3 y5 = y3 + y4 = 2 + 3 = 5 и т.д.
Получаем последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Слайд 20
Способы задания последовательности
Рекуррентное задание числовой
последовательности.
Выделяют 2 особенно важные рекуррентно заданные последовательности:
1) Арифметическая прогрессия
у1
= а, уn = уn-1 + d, а и d – числа, n = 2, 3, …
2) Геометрическая прогрессия
у1 = b, уn = уn-1 · q, b и q – числа, n = 2, 3, …
Слайд 21
Монотонные последовательности
Последовательность (уn ) – возрастающая, если каждый
ее член (кроме первого) больше предыдущего, т.е.
у1 < у2 < у3 < у4 < … < уn < …
Пример:
2, 4, 6, 8, 10, …
Если а > 1, то последовательность уn = аn – возрастает.
Последовательность (уn ) – убывающая, если каждый ее член (кроме первого) меньше предыдущего, т.е. у1 > у2 > у3 > у4 > … > уn > …
Пример:
-1, -3, -5, -7, -9, …
Если 0 < а < 1, то последовательность уn = аn – убывает.
Слайд 22
Монотонные последовательности
Возрастающие и убывающие последовательности называются монотонными.
Последовательности, которые
не возрастают и не убывают, являются немонотонными.