Слайд 2
Повторение теоретического материала по умк АО «Издательство «просвещение»
В
федеральный перечень учебников входят УМК:
Атанасян Л.С. «Геометрия 10-11» Базовый
и профильный уровни.
Погорелов А.В. «Геометрия 10-11» Базовый и профильный уровни.
Бутузов В.Ф. «Математика: алгебра и начала математического анализа, геометрия. ГЕОМЕТРИЯ 10-11 классы» Базовый и углублённый уровни.
Александров А.Д. «Математика: алгебра и начала математического анализа, геометрия. ГЕОМЕТРИЯ 10-11 классы» Базовый и углублённый уровни.
Слайд 3
Необходимо повторить теоретические факты стереометрии:
Плоскость может быть задана:
тремя
точками;
прямой и точкой;
двумя параллельными прямыми;
двумя пересекающимися прямыми.
Взаимное расположение двух
прямых в пространстве:
Две прямые могут быть параллельны, тогда они лежат в одной плоскости (может стоять задача о нахождении расстояния между ними).
Две прямые могут пересекаться, тогда они лежат в одной плоскости (может стоять задача о нахождении угла между ними).
Две прямые лежат в разных плоскостях (скрещивающиеся прямые). Может стоять задача о нахождении угла между скрещивающимися прямыми или расстояния между ними.
Слайд 4
Необходимо повторить теоретические факты стереометрии:
Взаимное расположение прямой и
плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость параллельны
(определение, признак параллельности прямой и плоскости). Может ставиться задача о нахождении расстояния от прямой до плоскости.
Прямая пересекает плоскость:
прямая перпендикулярна плоскости (определение, признак перпендикулярности прямой и плоскости);
прямая не перпендикулярна плоскости (проекция прямой на плоскость, угол между прямой и плоскостью, теорема о трёх перпендикулярах).
Слайд 5
Необходимо повторить теоретические факты стереометрии:
Взаимное расположение двух плоскостей
в пространстве:
Плоскости параллельны (определение, признак параллельности плоскостей, теоремы о
параллельности плоскостей). Может ставиться задача о нахождении расстояния между плоскостями.
Плоскости пересекаются (определение двугранного угла):
линейный угол двугранного угла;
плоскости перпендикулярны (определение, признак перпендикулярности плоскостей).
Слайд 6
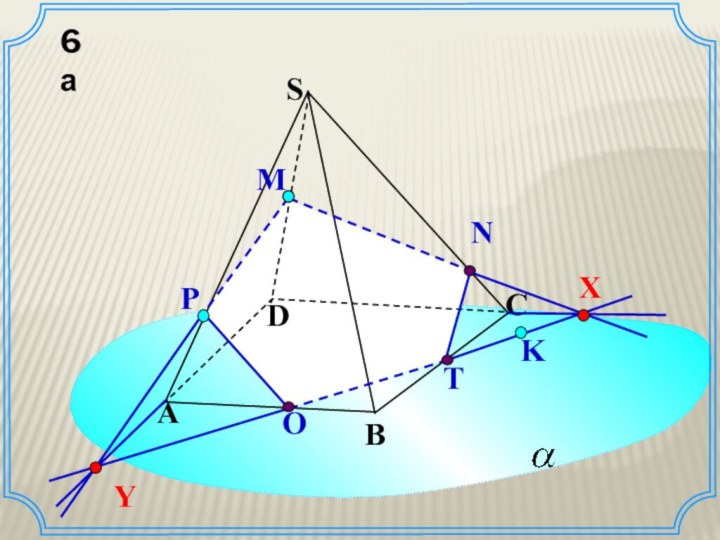
Чтобы решить задачу построения сечения многогранника ученик должен
знать:
что значит построить сечение многогранника плоскостью;
как могут располагаться относительно
друг друга многогранник и плоскость;
как задается плоскость;
когда задача на построение сечения многогранника плоскостью считается решенной.
построение плоскости сечения проходит в зависимости от задания этой плоскости.
Слайд 7
Условия, которыми может быть задана секущая плоскость:
построение сечения
многогранника плоскостью, проходящей через три точки;
построение сечения многогранника плоскостью,
проходящей через заданную точку параллельно заданной плоскости;
построение сечения, проходящего через заданную прямую параллельно другой заданной прямой (или через две точки параллельно заданной прямой);
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым.
Слайд 8
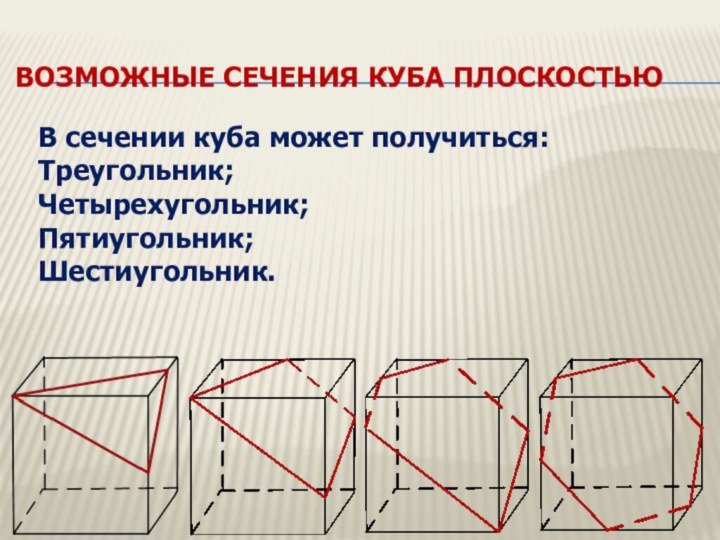
возможные сечения куба плоскостью
В сечении куба может
получиться:
Треугольник;
Четырехугольник;
Пятиугольник;
Шестиугольник.
Слайд 9
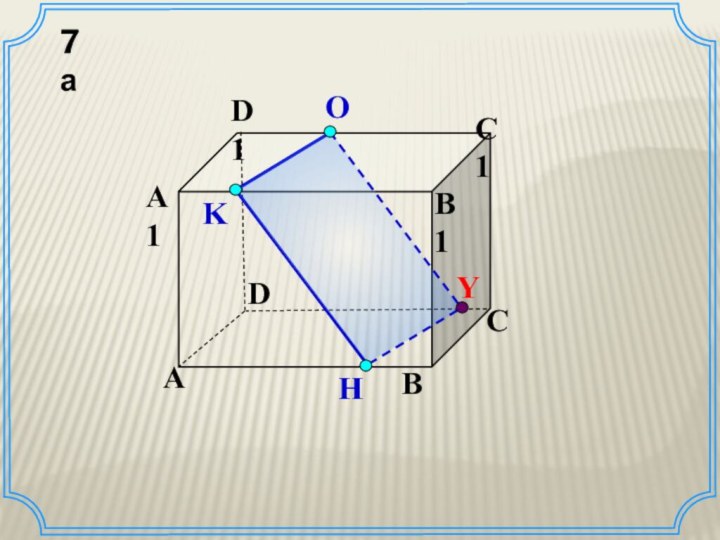
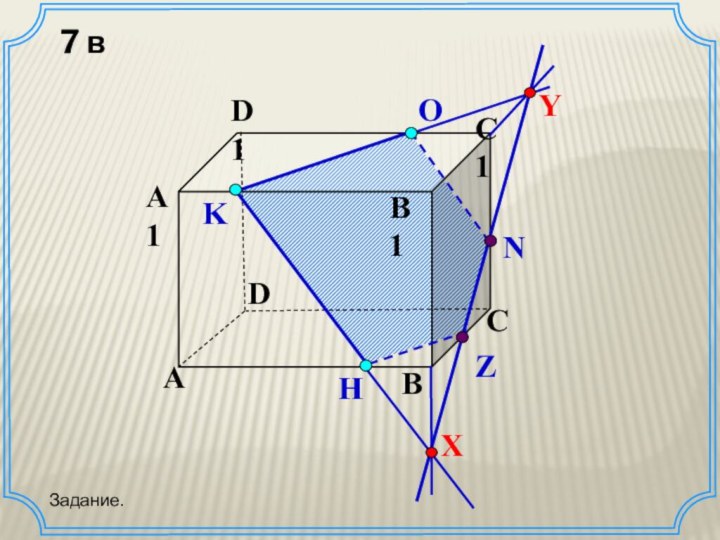
Правила построения сечений
Правило 1. Если две точки секущей
плоскости лежат в одной грани исходного тела (многогранника), то
соединяющий их отрезок является элементом искомого сечения.
Правило 2. Построенный элемент сечения можно параллельным переносом сдвинуть в принадлежащую искомому сечению точку параллельной грани данного многогранника.
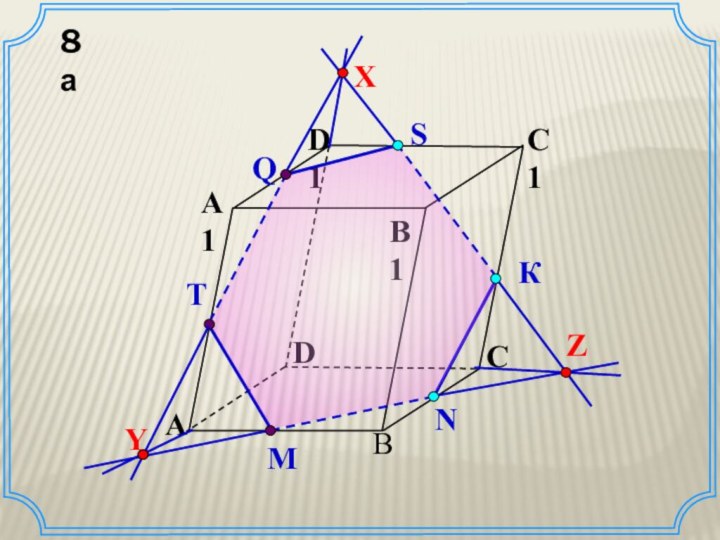
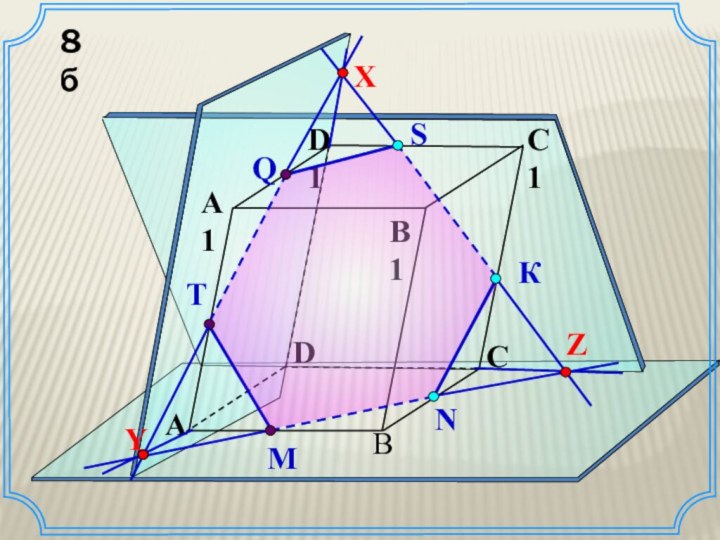
Правило 3. Если плоскость пересекает плоскость по прямой S , то прямую S называют следом плоскости на плоскости .
Слайд 10
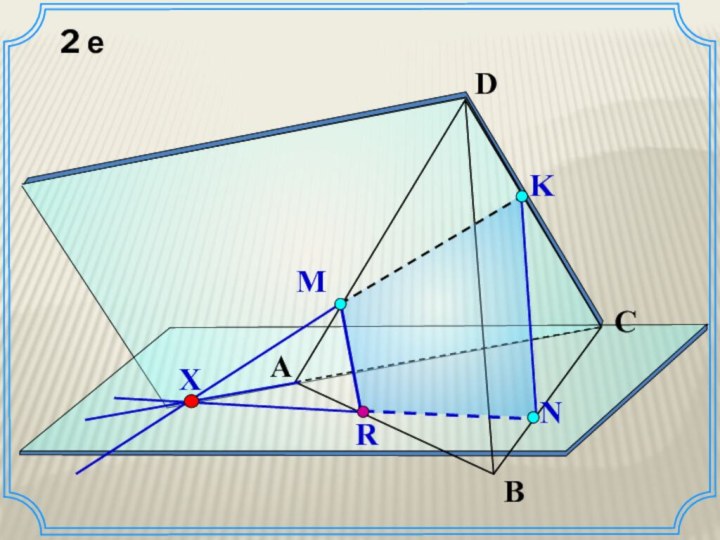
Метод Следа
заключается в построении следов секущей плоскости
на плоскость каждой грани многогранника. Построение сечения многогранника методом
следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.
Важное утверждение
Если точки P, Q и R принадлежат секущей плоскости и не лежат на одной прямой, а их проекциями на плоскость, выбранную в качестве основной, являются соответственно точки P1, Q1 и R1, то точки пересечения соответственных прямых: PQ и P1Q1, PR и P1R1, QR и Q1R1 лежат на одной прямой.
Слайд 11
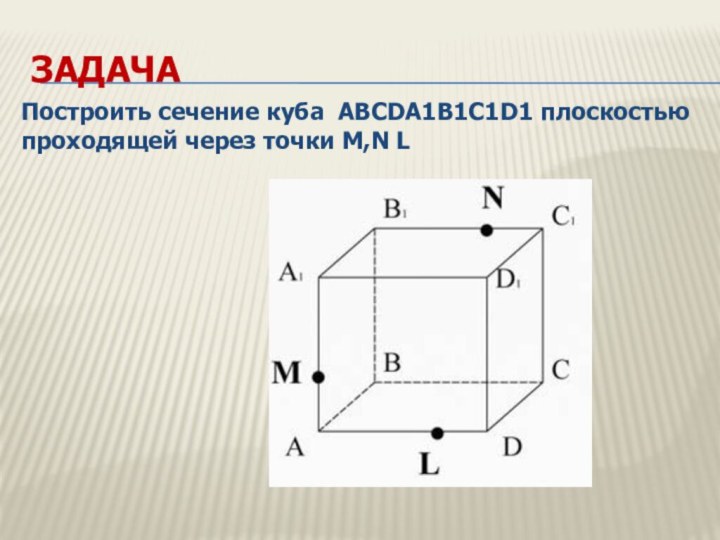
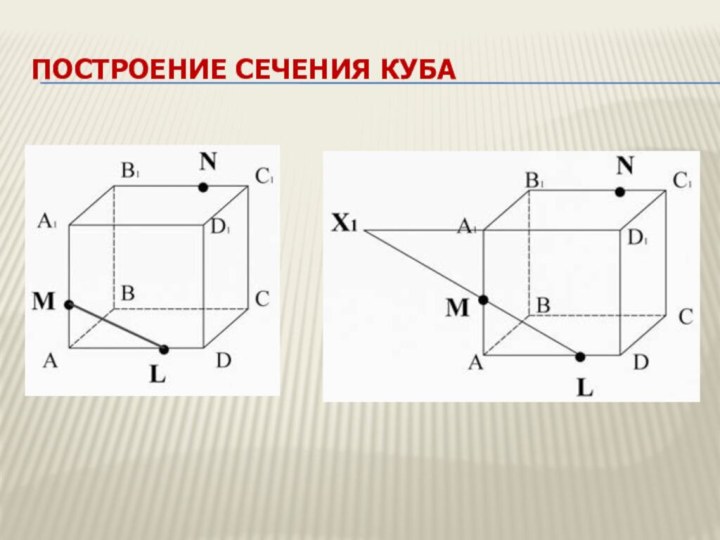
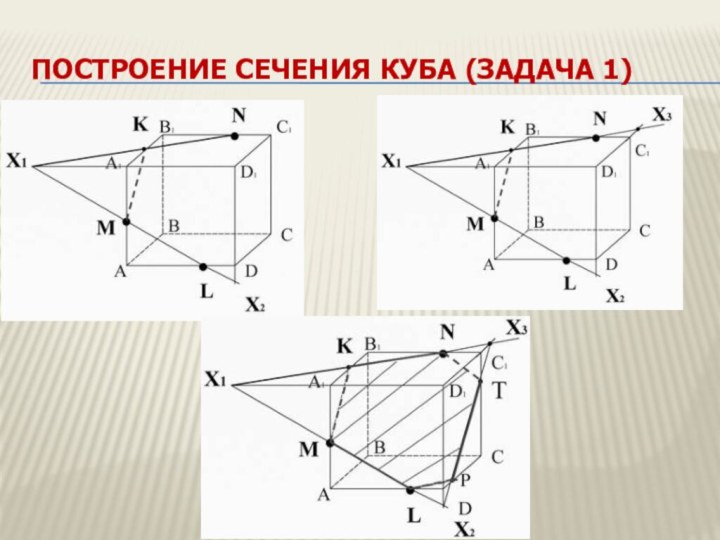
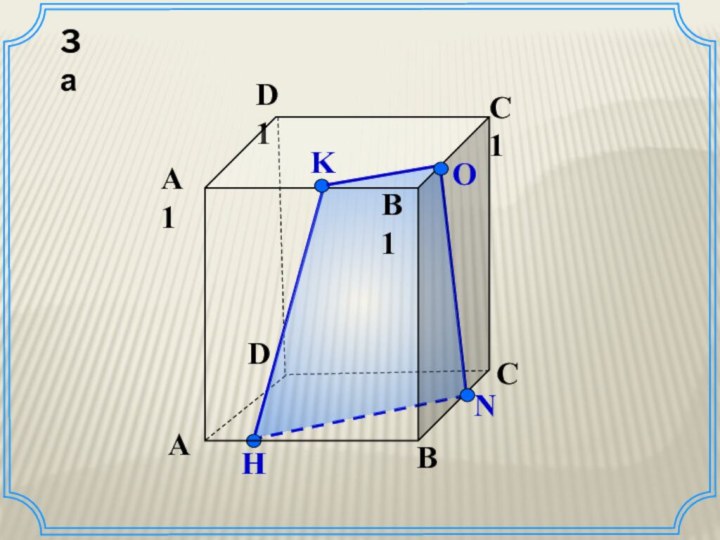
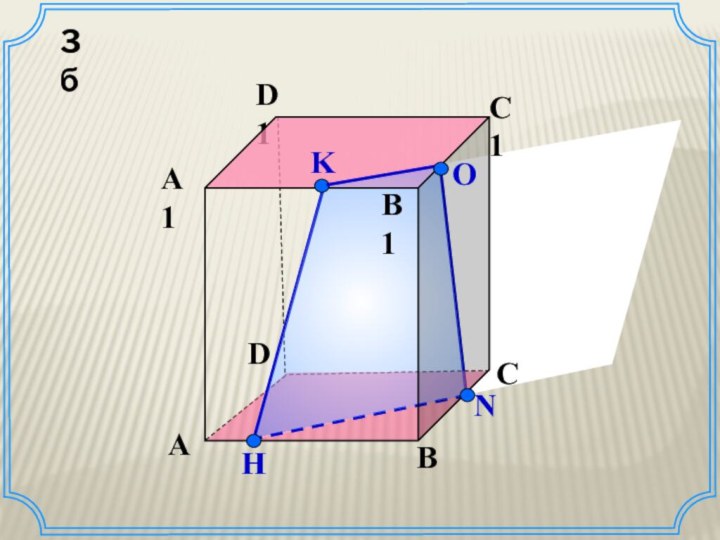
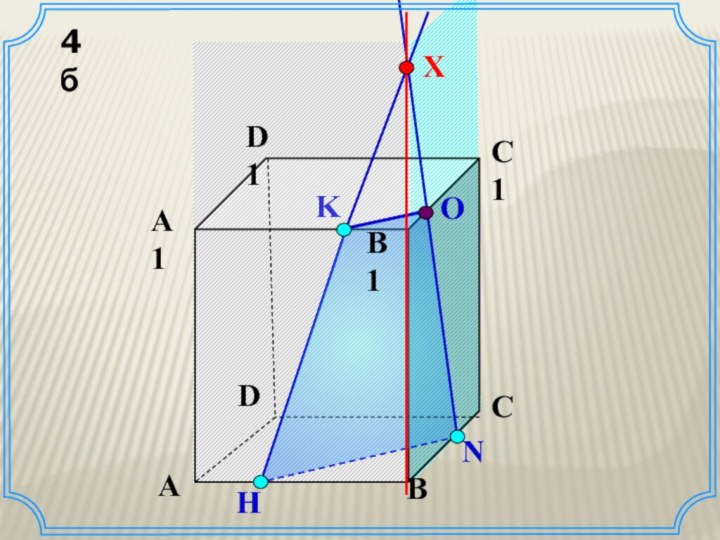
Задача
Построить сечение куба ABCDA1B1C1D1 плоскостью проходящей через
точки M,N L
Слайд 13
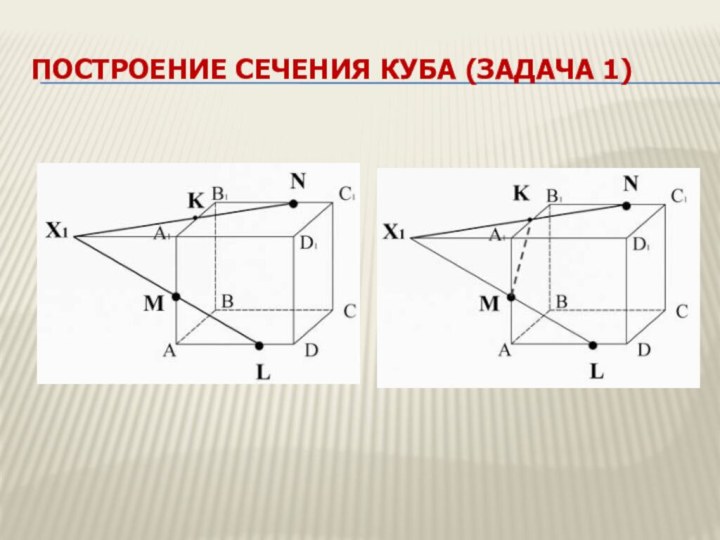
Построение сечения куба (задача 1)
Слайд 14
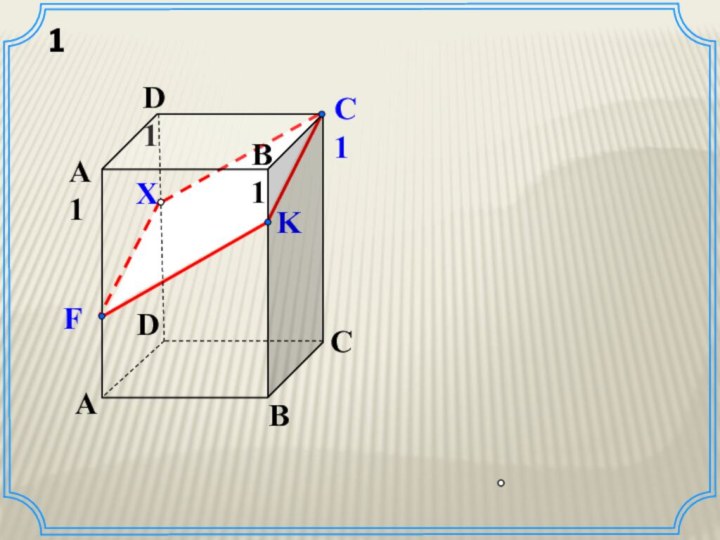
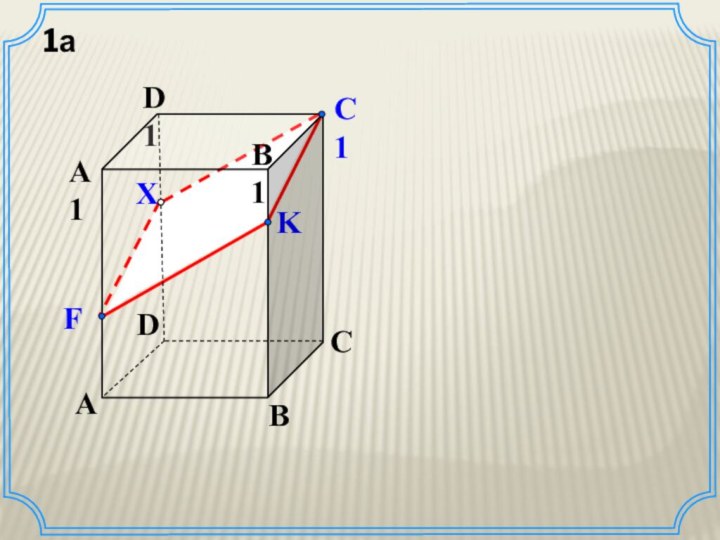
Построение сечения куба (задача 1)
Слайд 22
K
B
C
D
A
A1
D1
C1
B1
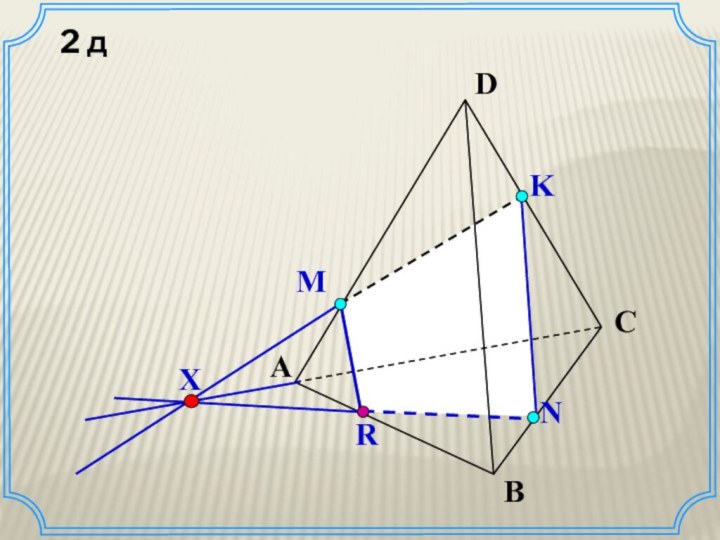
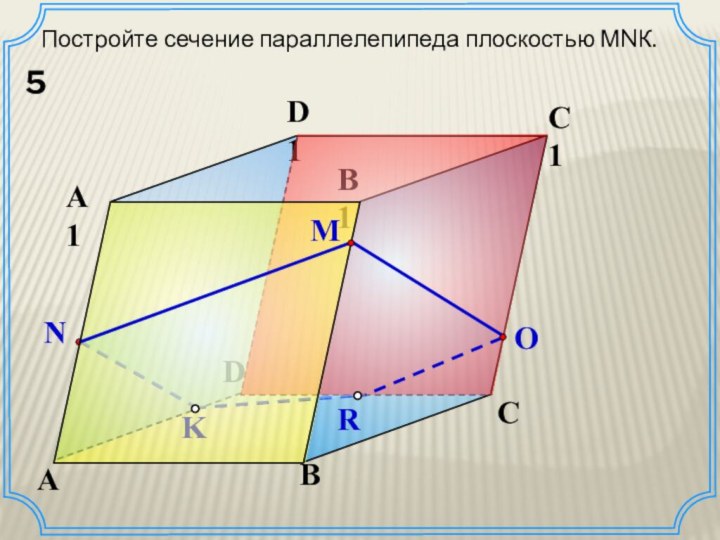
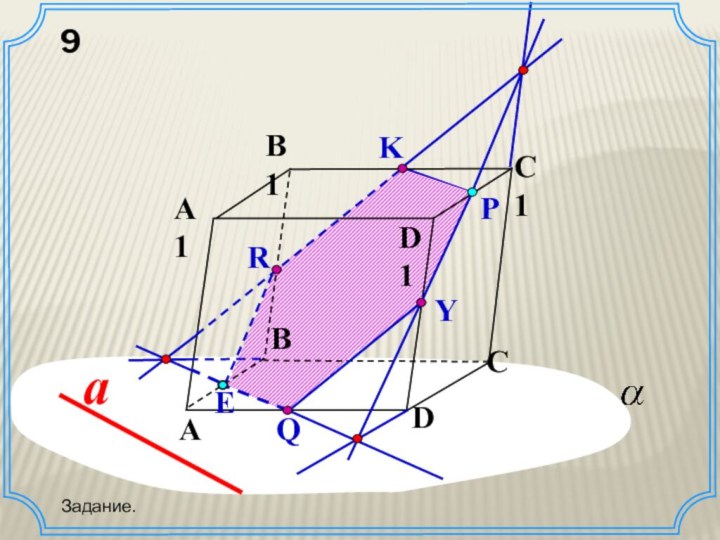
Постройте сечение параллелепипеда плоскостью МNК.
5