+ 16=0
x2 - 6x + 9 = 0
3x2 -
5x + 6 = 0x2 - 4 = 0
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

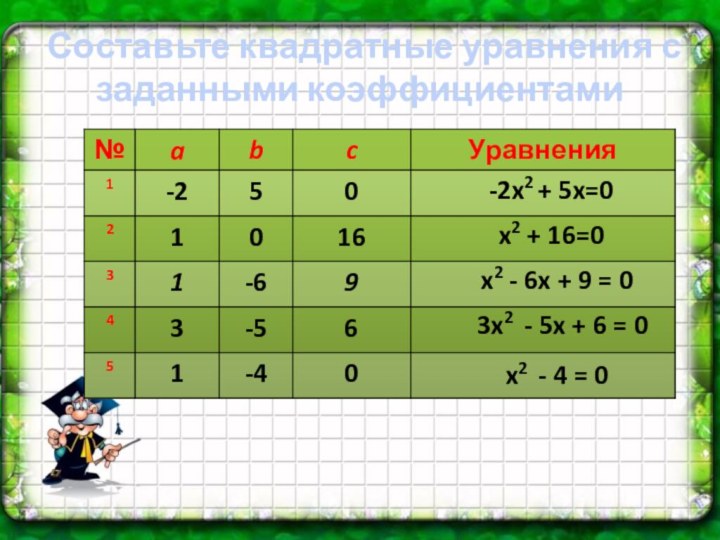














x2 - 4 = 0
3 способ. Решение квадратных
уравнений по формуле.
Например: x2 + 3x – 10 = 0
x 1· x 2 = – 10, значит корни имеют
разные знаки
x 1 + x 2 = – 3, значит больший по модулю
корень - отрицательный
Подбором находим корни: x 1 = – 5, x 2 = 2
x2+px+q=0
x 2= y 2 /a
При этом коэффициент a умножается на свободный член,
как бы «перебрасывается» к нему,
поэтому его и называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения,
используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
x 1 = 1
x 2 = с / a
Если в квадратном уравнении a + c = b, то
x 1 = - 1
x 2 = - с / a
Например: 137х2 + 20х – 157 = 0.
a = 137, b = 20, c = -157.
a + b+ c = 137 + 20 – 157 =0.
x1 = 1,
Ответ: 1;
x 1 = - a = - c
x 2 = - 1 / a = - 1 / c
Если в квадратном уравнении a = c и b = - (a2+1), то ,
x 1 = a = c
x 2 = 1 / a = 1 / c
3х² - 7х + 4 = 0;
х² - 22х – 23 = 0;
4 х² + 17 х + 4 = 0
4 х² + 17 х + 4 = 0
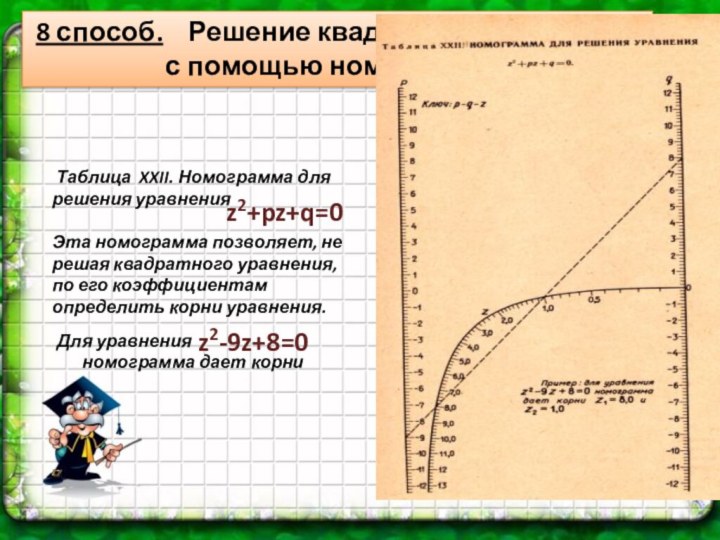
z2+pz+q=0
Для уравнения
номограмма дает корни
z2-9z+8=0
Рефлексия.