- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к исследовательской работе по теме: Квадратные уравнения
Содержание
- 2. Цель работы:разобрать существующие методы решения квадратных уравнений,
- 3. Задачи исследования- познакомиться с литературой по данной
- 4. Значимость проектаЗначимость: «Если я сделаю запланированное, то
- 5. Определить источники информации;Определить способы сбора и анализа
- 6. История квадратных уравнений1.Квадратные уравнения в Древнем Вавилоне2.Квадратные
- 7. Квадратные уравнения в Древнем ВавилонеНеобходимость решать уравнения
- 8. Правило решения этих уравнений, изложенное в вавилонских
- 9. Квадратные уравнения в ИндииЗадачи на квадратные уравнения
- 10. Квадратные уравнения у Аль-ХорезмиДля Аль-Хорезми, избегавшего употребления
- 11. Приведем пример.Задача 4. «Квадрат и число 21
- 12. Квадратные уравнения в Европе XII-XVII вФормы решения квадратных уравнений
- 13. Общее правило решения квадратных уравнений, приведенных к
- 14. Вывод формулы решения квадратного уравнения в общем
- 15. Разложение левой части уравнения на множители. Решим
- 16. Метод выделения полного квадрата. Решим уравнение х2
- 17. Решение квадратных уравнений по формулам. Умножим обе
- 18. Решение уравнений с использованием теоремы Виета. По
- 19. Решение уравнений способом «переброски». Рассмотрим квадратное уравнение
- 20. Графическое решение квадратного уравнения. Решение квадратных уравнений
- 21. Исследование В процессе исследования я провел следующие:
- 22. Скачать презентацию
- 23. Похожие презентации
Цель работы:разобрать существующие методы решения квадратных уравнений, провести анализ решения квадратных уравнений разными возрастами, создать шпаргалку по различным методам решения квадратных уравнений.




















Слайд 3
Задачи исследования
- познакомиться с литературой по данной теме;
-
сформулировать все определения, используемые при решении данной задачи;
- изучить
всевозможные способы решения квадратных уравнений, выявить плюсы и минусы;- принять участие в проводимом исследовании решения квадратных уравнений:
- подготовить компьютерную презентацию результатов работы.
Слайд 4
Значимость проекта
Значимость: «Если я сделаю запланированное, то приобрету
дополнительные знания, которыми смогу пользоваться на экзамене и в
дальнейшей жизни; студенты получат листовки-шпаргалки с формулами по которым решаются квадратные уравнения не стандартными методами».
Слайд 5
Определить источники информации;
Определить способы сбора и анализа информации;
Определить
способы представления результатов;
Выработать критерии оценки результатов и процесса работы.
план
работы:
Слайд 6
История квадратных уравнений
1.Квадратные уравнения в Древнем Вавилоне
2.Квадратные уравнения
в Индии
3.Квадратные уравнения у Аль-Хорезми
4.Квадратные уравнения в Европе XII-XVII в
5.Способы
решения квадратных уравнений
Слайд 7
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не
только первой, но и второй степени еще в древности
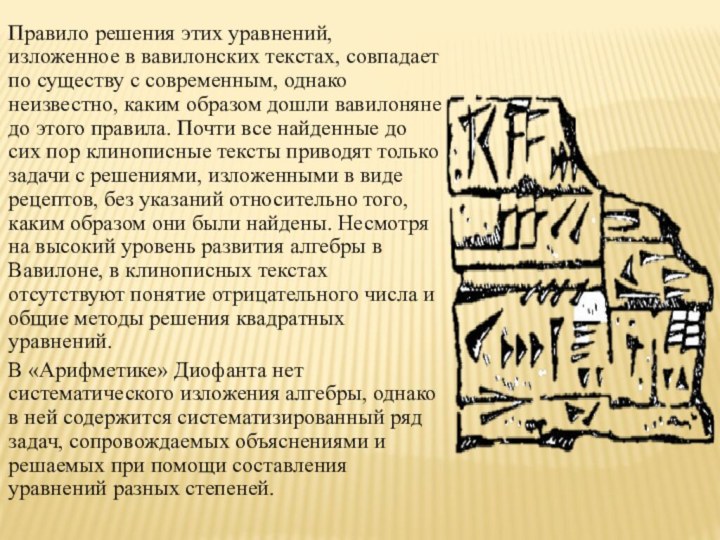
была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:Слайд 8 Правило решения этих уравнений, изложенное в вавилонских текстах,
совпадает по существу с современным, однако неизвестно, каким образом
дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Слайд 9
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются
уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г.
индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:ax2 + bх = с, а>
В уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
Слайд 10
Квадратные уравнения у Аль-Хорезми
Для Аль-Хорезми, избегавшего употребления отрицательных
чисел, члены каждого из этих уравнений слагаемые, а не
вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Слайд 11
Приведем пример.
Задача 4. «Квадрат и число 21 равны
10 корням. Найти корень» (подразумевается корень уравнения х2 +
21 = 10х).Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]
Слайд 12
Квадратные уравнения в Европе XII-XVII в
Формы решения квадратных уравнений по
образцу Аль-Хорезми в Европе были впервые изложены в «Книге
абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв.
Слайд 13 Общее правило решения квадратных уравнений, приведенных к единому
каноническому виду x2 + bх = с при всевозможных
комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.Слайд 14 Вывод формулы решения квадратного уравнения в общем виде
имеется у Виета, однако Виет признавал только положительные корни.
Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Слайд 15
Разложение левой части уравнения на множители.
Решим уравнение х2
+ 10х - 24 = 0.
Разложим левую часть
на множители:х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.
х + 12= 0 или х – 2=0
х=-12 х=2
Ответ: -12; 2.
Слайд 16
Метод выделения полного квадрата.
Решим уравнение х2 + 6х
- 7 = 0.
Выделим в левой части полный
квадрат: х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
тогда, данное уравнение можно записать так:
(х + 3)2 - 16 =0,
(х + 3)2 = 16.
х + 3=4 или х + 3 = -4
х1 = 1 х2 = -7
Ответ: 1; -7.
Слайд 17
Решение квадратных уравнений по формулам.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠
0на 4а, тогда4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
1. Таким образом, в случае положительного дискриминанта, т.е. при b2 - 4ac >0, уравнение ах2 + bх + с = 0 имеет два различных корня.
2. Если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение имеет один корень .
3. Если дискриминант отрицателен, т.е. b2 - 4ac < 0, уравнение ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
Слайд 18
Решение уравнений с использованием теоремы Виета.
По праву достойна
в стихах быть воспета
О свойствах корней теорема Виета.
Приведенным квадратным
уравнением называется уравнение вида где старший коэффициент равен единице.Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Слайд 19
Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 +
bх + с = 0, где а ≠ 0.
Умножая
обе его части на а, получаем уравнение а2х2 + аbх + ас = 0.Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0,
равносильно данному.
Его корни у1 и у2 найдем с помощью теоремы Виета и окончательно:
х1 = у1/а и х1 = у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Слайд 20
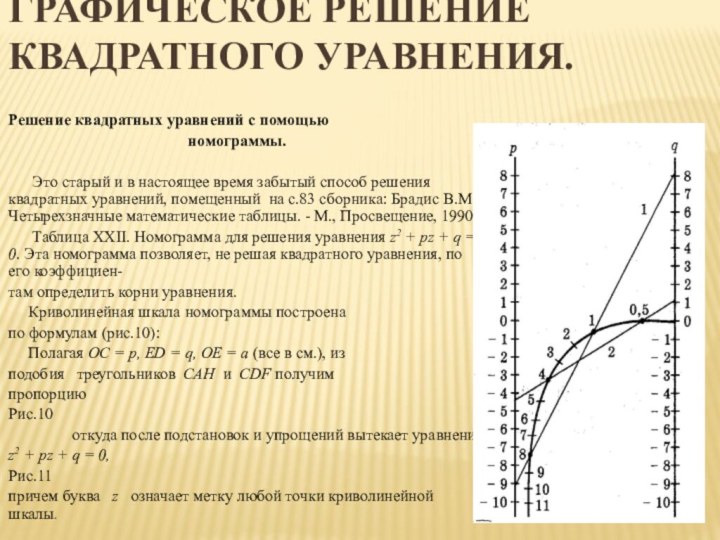
Графическое решение квадратного уравнения.
Решение квадратных уравнений с помощью
номограммы.
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990.
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-
там определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.10):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
пропорцию
Рис.10
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,
Рис.11
причем буква z означает метку любой точки криволинейной шкалы.
Слайд 21
Исследование
В процессе исследования я провел следующие:
- нашёл
нужную литературу;
составил квадратные уравнения;
- раздал уравнения обучающимся 1 курса,
для решения им и их родственникам (родители, бабушки, дедушки, дяди, тети).- проверил решения предоставленные испытуемыми;
- обработал результаты:
Из 4 групп первого курса принимавших участие в эксперименте 80 человек, их родственники 50 человек. При обработке результатов было видно, что все испытуемые использовали один и тот же способ решения квадратных уравнений с помощью формул ( находили дискриминант), правильных решений уравнений с помощью дискриминанта в возрастной группе от 15 до 17 лет было 81,25 %, не верных 18,75. Во второй возрастной группе от 18 до 60 лет было решено верно 34 % не решено или решено не верно 66%.





























