- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему для учителя по теме: Задача коммивояжера. Факультативное занятие по математике. 8 класс
Содержание
- 2. Задача коммивояжераКоммивояжёр (фр. commis voyageur) — бродячий торговец. Задача коммивояжёра — важная
- 3. Задача коммивояжераЭто оптимальный маршрут коммивояжёра через 15
- 4. Задача коммивояжераТочно неизвестно, когда проблему коммивояжера исследовали
- 5. Задача коммивояжераРанним вариантом задачи может рассматриваться задача Уильяма Гамильтона 19
- 6. Задача коммивояжераСовершенно очевидно, что задача может быть
- 7. Задача коммивояжераМожет быть, алгоритм, основанный на полном переборе
- 8. Задача коммивояжераДля возможности применения математического аппарата для
- 9. Задача коммивояжераГамильтоновым циклом называется маршрут, включающий ровно по
- 10. Симметричная задача для четырёх городовМаршрутом (также гамильтоновым
- 11. Задача коммивояжераРазличают различные варианты задачи, важнейшими из которых являются симметричная и метрическая задачи.
- 12. Задача коммивояжераВ данной презентации использованы материалы следующих
- 13. Скачать презентацию
- 14. Похожие презентации
Задача коммивояжераКоммивояжёр (фр. commis voyageur) — бродячий торговец. Задача коммивояжёра — важная задача транспортной логистики, отрасли, занимающейся планированием транспортных перевозок. Коммивояжёру, чтобы распродать нужные в хозяйстве товары, следует объехать n пунктов и в конце концов вернуться в исходный пункт. Требуется определить наиболее выгодный маршрут объезда. В качестве меры










![Презентация для учителя по теме: Задача коммивояжера. Факультативное занятие по математике. 8 класс Задача коммивояжераВ данной презентации использованы материалы следующих сайтов:Задача коммивояжёра [Электронный ресурс] –](/img/tmb/7/667182/43615918ecd4e323f09d221adae0f6a8-720x.jpg)

Слайд 2
Задача коммивояжера
Коммивояжёр (фр. commis voyageur) — бродячий торговец. Задача коммивояжёра — важная задача транспортной
Слайд 3
Задача коммивояжера
Это оптимальный маршрут коммивояжёра через 15 крупнейших
городов Германии. Указанный маршрут является самым коротким из всех
возможных 43 589 145 600 вариантов.
Слайд 4
Задача коммивояжера
Точно неизвестно, когда проблему коммивояжера исследовали впервые.
Однако, известна изданная в 1832 году книга с названием «Коммивояжёр — как он
должен вести себя и что должен делать для того, чтобы доставлять товар и иметь успех в своих делах — советы старого курьера», в которой описана проблема, но математический аппарат для её решения не применяется. Зато в ней предложены примеры маршрутов для некоторых регионов Германии и Швейцарии.
Слайд 5
Задача коммивояжера
Ранним вариантом задачи может рассматриваться задача Уильяма Гамильтона 19 века,
которая заключалась в том, чтобы найти маршруты на графе
с 20 узлами. Первые упоминания в качестве математической задачи на оптимизацию принадлежат Карлу Менгеру.Больших успехов удалось достичь в конце 1970-х и 1980-х годах, когда Мартин Грётчел, Манфред Падберг и Джованни Ринальди и другие, с применением новых методов деления плоскостью, ветвей и границ вычислили решение для отдельного случая задачи с 2393 городами.
В марте 2005 года задача с 33 810 узлами была решена программой Конкорд: был вычислен путь длиной в 66 048 945 и доказано отсутствие более коротких путей.
Слайд 6
Задача коммивояжера
Совершенно очевидно, что задача может быть решена
перебором всех вариантов объезда и выбором оптимального. Беда в том,
что количество возможных маршрутов очень быстро возрастает с ростом n (оно равно n! — количеству способов упорядочения пунктов). К примеру, для 100100 пунктов количество вариантов будет представляться 158-значным числом.
Слайд 7
Задача коммивояжера
Может быть, алгоритм, основанный на полном переборе вариантов,
не является самым эффективным (в смысле быстродействия) для решения задачи коммивояжёра?
Увы, доказано, что не существует алгоритма решения, имеющего степенную сложность (то есть требующего порядка na операций для некоторого a) — любой алгоритм будет хуже.В таком случае следует отказаться от попыток отыскать точное решение задачи коммивояжёра и сосредоточиться на поиске приближённого — пускай не оптимального, но хотя бы близкого к нему. В виду большой практической важности задачи полезными будут и приближённые решения.
Слайд 8
Задача коммивояжера
Для возможности применения математического аппарата для решения
проблемы её следует представить в виде математической модели. Проблему коммивояжёра
можно представить в виде модели на графе, то есть, используя вершины и ребра между ними. Таким образом, вершины графа соответствуют городам, а рёбра (i, j) между вершинами i и j — пути сообщения между этими городами. Каждому ребру (i, j) можно сопоставить критерий выгодности маршрута cij≥0, который можно понимать как, например, расстояние между городами, время или стоимость поездки.
Слайд 9
Задача коммивояжера
Гамильтоновым циклом называется маршрут, включающий ровно по одному
разу каждую вершину графа.
В целях упрощения задачи и гарантии
существования маршрута обычно считается, что модельный граф задачи является полностью связным, то есть, что между произвольной парой вершин существует ребро. В тех случаях, когда между отдельными городами не существует сообщения, этого можно достичь путём ввода рёбер с максимальной длиной. Из-за большой длины такое ребро никогда не попадет к оптимальному маршруту, если он существует.Таким образом, решение задачи коммивояжёра — это нахождение гамильтонова цикла минимального веса в полном взвешенном графе.
Слайд 10
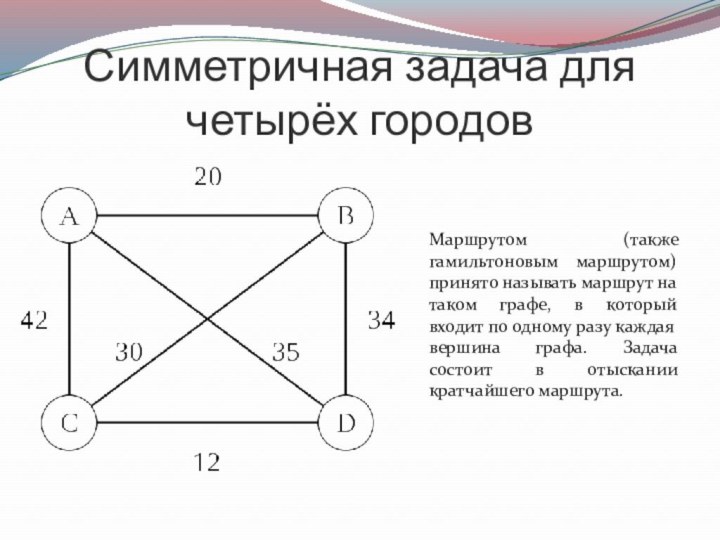
Симметричная задача для четырёх городов
Маршрутом (также гамильтоновым маршрутом)
принято называть маршрут на таком графе, в который входит
по одному разу каждая вершина графа. Задача состоит в отыскании кратчайшего маршрута.
Слайд 11
Задача коммивояжера
Различают различные варианты задачи, важнейшими из которых
являются симметричная и метрическая задачи.
Слайд 12
Задача коммивояжера
В данной презентации использованы материалы следующих сайтов:
Задача
коммивояжёра [Электронный ресурс] – Доступ: http://math.msu.su/~shvetz/54/inf/perl-problems/chCommisVoyageur.xhtml#chCommisVoyageur_sCommons
Задача коммивояжёра [Электронный ресурс]
– Доступ: https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%BA%D0%BE%D0%BC%D0%BC%D0%B8%D0%B2%D0%BE%D1%8F%D0%B6%D1%91%D1%80%D0%B0Задача коммивояжёра [Электронный ресурс] – Доступ: http://referatwork.ru/category/programmirovanie/view/610714_predstavlenie_v_vide_grafa





























