в точке х₀
тангенс угла наклона касательной к положительному направлению
оси ОХугловой коэффициент касательной
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


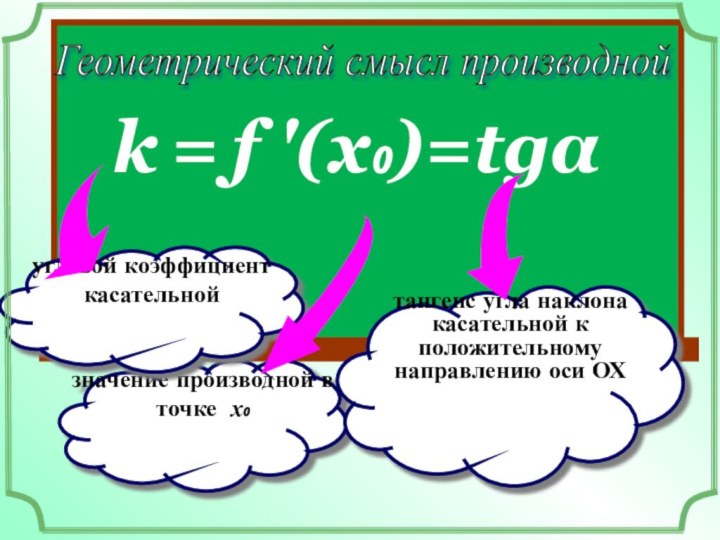













угловой коэффициент касательной
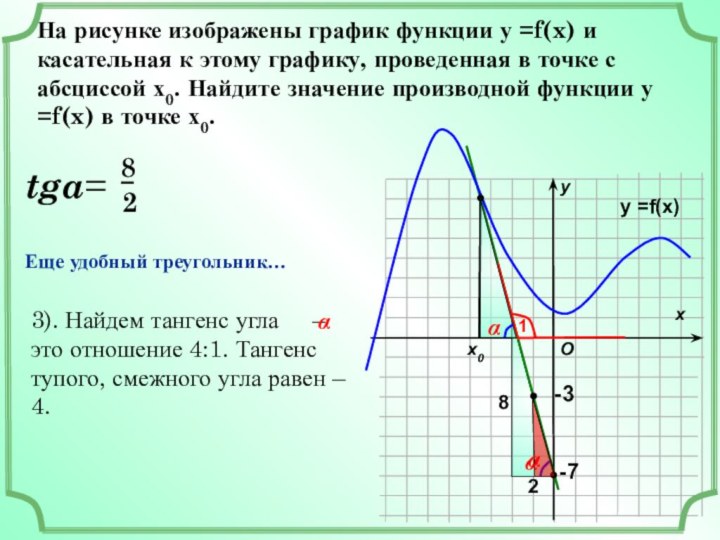
х
х0
у
O
у =f(x)
-3
-7
Еще удобный треугольник…
(-1; -3)
(0; -7)
– 7 = b.
– 3 = – 1k + b.
– 4 = k
k = – 4
Вывод уравнения касательной
Вывод уравнения касательной
ордината точки касания (значение функции y=f(x) в точке x0)
абсцисса точки касания
y=ln2x, x0=e.
y= f ′(x0)·(x- x0)+ f(x0)
y0=1.
y= f ′(x0)·(x- x0)+ f(x0)
y= f ′(x0)·(x- x0)+ f(x0)
у = e2x-1, y=2x+7
y= f ′(x0)·(x- x0)+ f(x0)