- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку алгебры в 9 классе Сумма п первых членов арифметической прогрессии
Содержание
- 2. Цель урока: ознакомление учащихся с выводом формул суммы n первых членов арифметической прогрессии и формирование умения применения формул при решении задач.
- 3. Задачи урока:Учебная: познакомить учащихся с формулой суммы
- 4. Немного из историиСлово «прогрессия» латинского происхождения (progressio),
- 5. Устный счет
- 6. Арифметическая прогрессияЗадания для устного счетаУпражнение 169 класс
- 7. Найдите разность арифметической прогрессииПравильный ответ:415-5-73
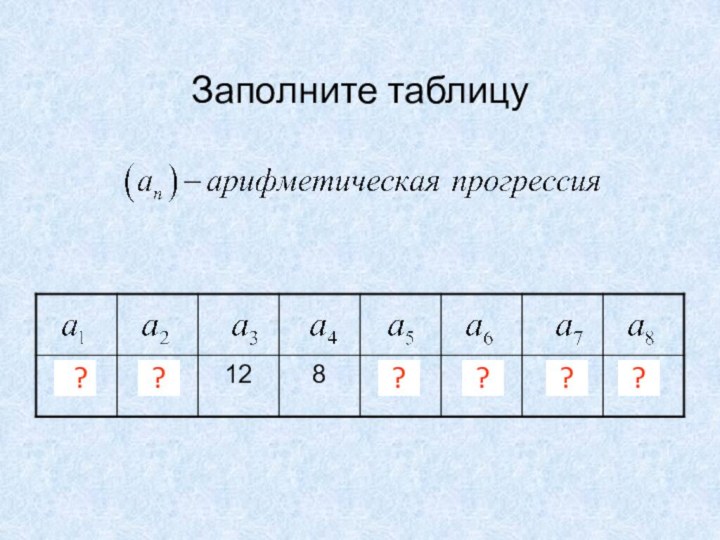
- 8. Заполните таблицу??????
- 9. Заполните таблицу??????
- 10. Заполните таблицу??????Закрыть
- 11. редыдущийпоследовательностьрмоннтныйррукерченокаяолььсонзарчитемфиралнычПроверь себяПо горизонталиПервый из двух стоящих рядом
- 12. ИГРА «ЛОТО»Выбирай правильный ответ, и у тебя получится красивая картинка… Начинаем
- 13. Из предложенных последовательностей выберите ту, которая может
- 14. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 523564202530
- 15. Чему равна разность арифметической прогрессии: -2; 1; 4; 35643-15
- 16. 564-41618Укажите n-ый член арифметической прогрессии, если d=2, n=4, а1 =10
- 17. Найдите восьмой член последовательности, заданной формулой аn =n*(n-1)56473656
- 18. Найдите двадцать третий член арифметической прогрессии ( ап ), если а1= 15 и d = 3.81396846
- 19. Молодцы!
- 20. Из истории математики: С формулой суммы
- 21. Когда ему было 9 лет, учитель, занятый
- 22. Как Гауссу удалось так быстро сосчитать сумму такого большого количества чисел?
- 23. Попытаемся найти ответ на данный вопрос.
- 24. З А Д А Н И
- 25. Давным-давно сказал один мудрецЧто прежде надоСвязать начало и конецУ численного ряда.
- 26. Вот схема рассуждений Гаусса. Сумма чисел в каждой
- 27. Тема урока: Сумма n-первых членов арифметической прогрессии
- 28. аn) – арифметическая прогрессия. Sn = a1
- 29. Арифметическая прогрессия
- 30. Тренировочные упражнения:1. (an) – арифметическая прогрессия.a1 = 6, a5 = 26. Найти S5.
- 31. Решение: Sn = (а1+а5) : 2
- 32. 2. (an) – арифметическая прогрессия. a1 = 12, d = - 3. Найти S16.
- 33. Решение: S16 = (а1+а16):2×16 Заметим,
- 34. Работа по учебнику.Решить № 16.33 (в; г)
- 35. Работа по учебнику.1. Решить № 16.33 (в;
- 36. Самостоятельная работа:
- 37. Домашнее задание изучить по учебнику материал на
- 38. «Что есть больше всего на свете?
- 39. Спасибо за урок!
- 40. Скачать презентацию
- 41. Похожие презентации
Цель урока: ознакомление учащихся с выводом формул суммы n первых членов арифметической прогрессии и формирование умения применения формул при решении задач.
Слайд 2
Цель урока:
ознакомление учащихся с выводом формул суммы n первых членов арифметической прогрессии и
формирование умения применения формул при решении задач.
Слайд 3
Задачи урока:
Учебная: познакомить учащихся с формулой суммы n-первых
членов арифметической прогрессии, создать условия для формирования умений решать
задачи на применениеВоспитательная: воспитывать интерес к истории математики.
Развивающая: развивать любознательность и вычислительные навыки.
Слайд 4
Немного из истории
Слово «прогрессия» латинского происхождения (progressio), буквально
означает «движение вперед» ( как и слово «прогресс») и
встречается впервые у римского автора Боэция (V-VI вв.).Правило для нахождения суммы членов произвольной арифметической прогрессии даётся в «Книге абака» (1202г.) Леонардо Фибоначчи.
Слайд 11
р
е
д
ы
д
у
щ
и
й
п
о
с
л
е
д
о
в
а
т
е
л
ь
н
о
с
т
ь
р
м
о
н
н
т
н
ы
й
р
р
у
к
е
р
ч
е
н
о
к
а
я
о
л
ь
ь
с
о
н
з
а
р
ч
и
т
е
м
ф
и
р
а
л
н
ы
ч
Проверь себя
По горизонтали
Первый из двух стоящих рядом членов
последовательности
2. Разность последовательно одинаковых членов
3.
Способ задания последовательности4. Число в арифметической прогрессии
5. Элементы, из которых состоит последовательность
6. Натуральное число, обозначающее место члена в последовательности
По вертикали
1. Функция, заданная на множестве натуральных чисел
7. Вид прогрессии
8. Последовательность, содержащая конечное число членов
с
к
а
я
1
2
3
4
5
6
7
8
Слайд 13 Из предложенных последовательностей выберите ту, которая может являться
арифметической прогрессией.
1
2
3
5
6
4
1; 2; 4; 9; 16…
1; 11; 21; 31…
2;
4; 8; 16…Слайд 14 Какое из этих чисел является шестым членом последовательности
натуральных чисел, кратных 5
2
3
5
6
4
20
25
30
Слайд 18 Найдите двадцать третий член арифметической прогрессии ( ап
), если а1= 15 и d = 3.
81
396
84
6
Слайд 20
Из истории математики:
С формулой суммы n
первых членов арифметической прогрессии был связан эпизод из жизни
немецкого математика К. Ф. Гаусса (1777 – 1855).Слайд 21 Когда ему было 9 лет, учитель, занятый проверкой
работ учеников других классов, задал на уроке следующую задачу:
«Сосчитать сумму натуральных чисел от 1 до 100 включительно: 1 + 2 + 3 + … +100. Каково же было удивление учителя, когда один из учеников (это был Гаусс) через минуту воскликнул: «Я уже решил…»Большинство учеников после долгих подсчетов получили неверный результат. В тетради Гаусса было написано одно число и притом верное.
Слайд 24
З А Д А Н И Е
Задача
очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить
в уме все числа?Пять первых связок изучи,
Найдешь к решению ключи!
101
101
101
101
101
Слайд 26
Вот схема рассуждений Гаусса.
Сумма чисел в каждой паре
101. Таких пар 50, поэтому искомая сумма равна
101×50 =
5050.Попытаемся понять как ему это удалось. Выведем формулу суммы n первых членов арифметической прогрессии.
Слайд 28 аn) – арифметическая прогрессия. Sn = a1 + a2
+ a3 + a4 + … + an-1 +
an, Sn = an + an-1 +an-2 + an-3 + … =a2 + a1 a2 + an-1 = (a1 + d) + (an – d) = a1 + an, a3 + an-2 = (a2 + d) + (an-1 – d) = a2 + an-1 = a1 + an, a4 + an-3 = (a3 + d) + (an-2 – d) = a3 + an-2 = a1 + an и т.д. 2Sn = (a1 + an)n. Sn = (a1 + an)n : 2 – формула суммы n первых членов арифметической прогрессии. Sn = (a1 + an)n : 2 , an = a1 + d(n – 1) Sn = (a1 + a1 + d(n-1))n : 2 = (2a1 + d(n – 1))n : 2 Sn = (2a1 + d(n – 1))n : 2 – формула суммы n первых членов арифметической прогрессии.Слайд 31 Решение: Sn = (а1+а5) : 2 × 5 Теперь
вычислим сумму пяти первых членов арифметической прогрессии: S5 =
(6+26) : 2 × 5=80. Ответ: 80.Слайд 33 Решение: S16 = (а1+а16):2×16 Заметим, что в данной
прогрессии не задан последний член этой суммы. Найдем 16
член прогрессии: а16 = 12+ 15×(-3) =12+(-45) =-33 Теперь вычислим сумму: S16 = (12+ (-33)) ×16: 2 = (-21) ×8 = -168. Ответ: -168. При решении таких задач можно воспользоваться второй формулой S16 =(2а1 +d( n -1)):2×16 =(2×12+15×(-3)):2×16 =-21:2×16 = -168. Ответ: - 168.
Слайд 34
Работа по учебнику.
Решить № 16.33 (в; г) с
комментированием на месте.
Решить № 16.35 (в; г)
по формуле (II): Решить № 16.37 (в; г) на доске и в тетрадях.
Слайд 35
Работа по учебнику.
1. Решить № 16.33 (в; г)
с комментированием на месте.
в) S10 = –90.
г) S25
= 600.3. Решить № 16.35 (в; г) по формуле (II):
О т в е т: в) 2350; г) –6175.
4. Решить № 16.37 (в; г) на доске и в тетрадях.
в) аn = –2n + 8; а1 = –2 × 1 + 8 = 6; а30 = –2 × 30 + 8 = –52;
г) аn = –2,5n – 6; а1 = –8,5; а30 = –2,5 × 30 – 6 = –81;
О т в е т: в) –690; г) –1342,5.
Слайд 37
Домашнее задание
изучить по учебнику материал на с.
151–154 и записать в тетради решение примеров 7 и
8; решить № 16.33 (а; б) – 16.35 (а; б); № 16.37 (а; б).Слайд 38 «Что есть больше всего на свете? - Пространство. Что
