Презентация на тему Производная

в который ты не усвоил ничего нового и ничего

Я. А. Коменский

геометрический и физический смысл производной; уравнение касательной к графику функции; применение

выполнять действия с функциями (описывать по графику поведение и свойства функции, находить её наибольшее и наименьшее значения).

5х + 8.

2. Вычислить производную у = (2х –

(x), и касательная к нему в точке с абсциссой

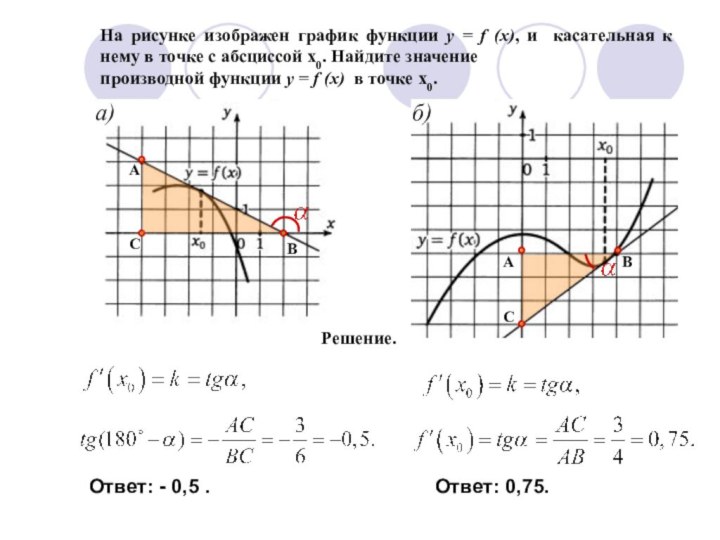
Решение.

Ответ: - 0,5 .

Ответ: 0,75.

С

В

А

a)

б)

4 5 6 7
-7 -6 -5

4
3
2
1

-1
-2
-3
-4
-5

y

x

+

–

–

+

+

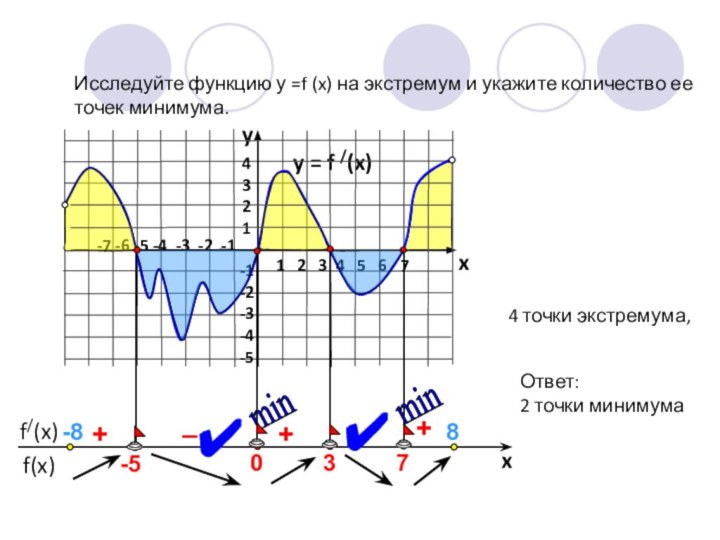
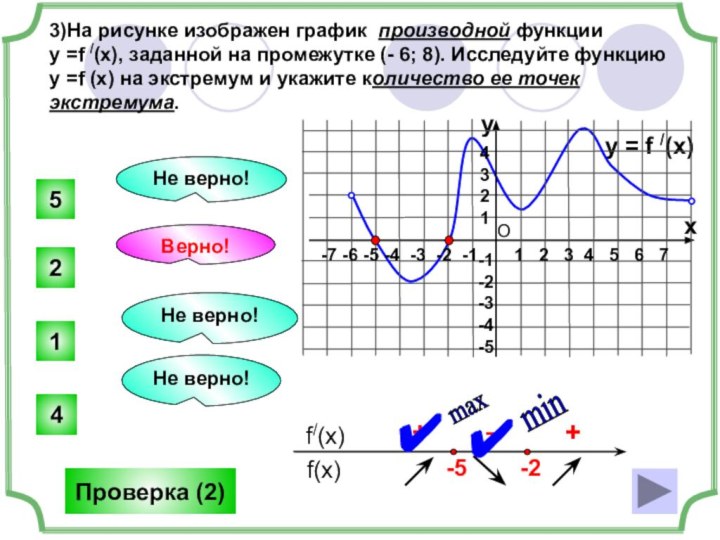
Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.

4 точки экстремума,

Ответ:
2 точки минимума

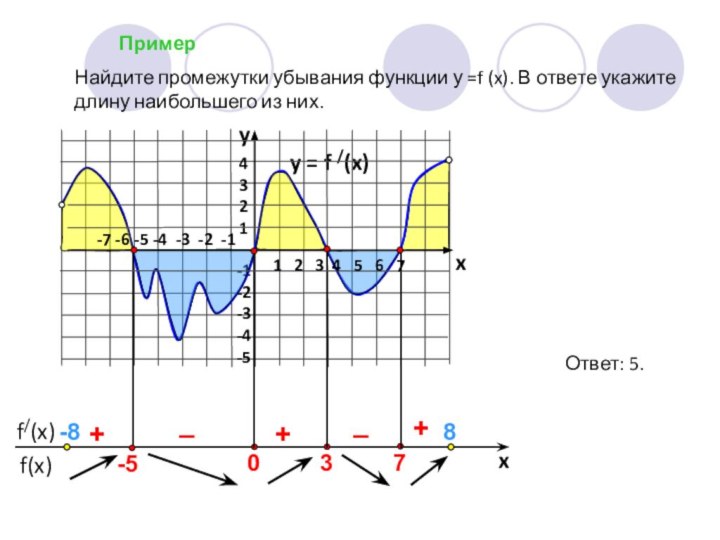
-8

8

=f (x).
В точках –5, 0, 3 и 7
функция

1 2 3 4 5 6 7

-7 -6 -5 -4 -3 -2 -1

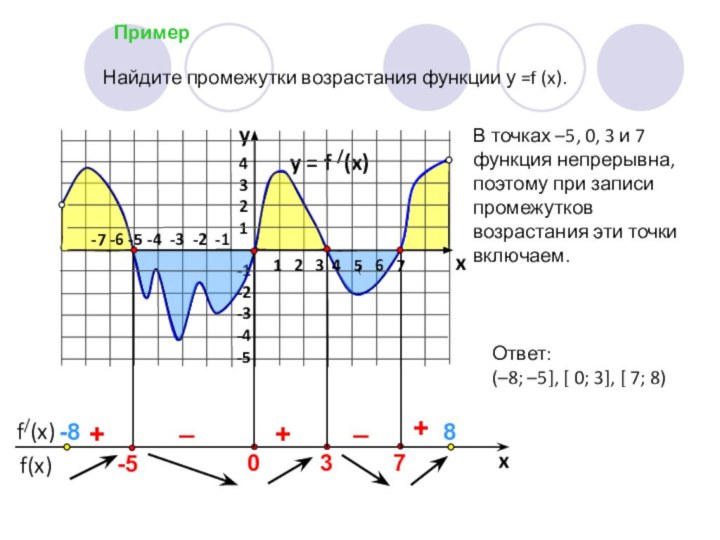
Ответ:
(–8; –5], [ 0; 3], [ 7; 8)

-8

8

=f (x). В ответе укажите длину наибольшего из них.

1 2 3 4 5 6 7

-7 -6 -5 -4 -3 -2 -1

Ответ: 5.

-8

8

На рисунке изображен график функции

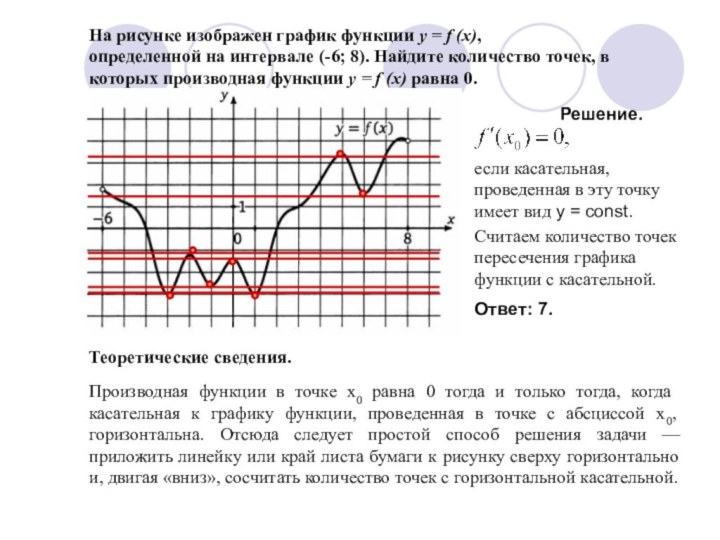
Решим эту задачу, воспользовавшись следующим утверждением. Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) не положительна (не отрицательна). Значит необходимо выделить промежутки убывания функции и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков.

Решение.

Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.

Ответ: 4.

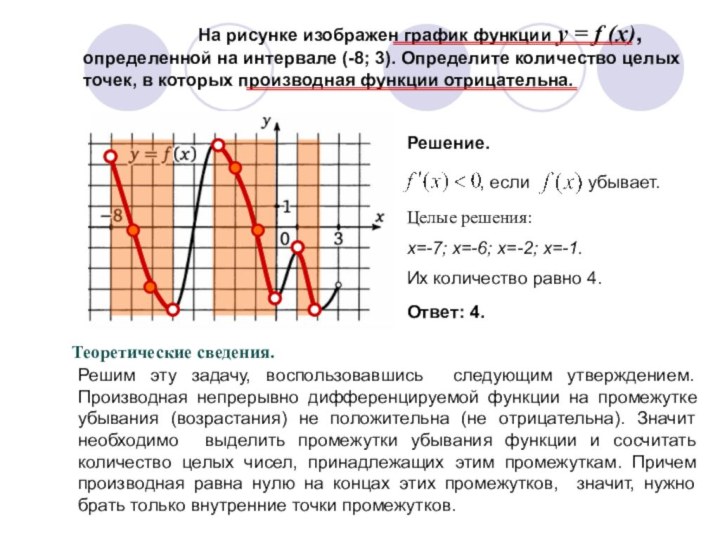
Теоретические сведения.

(x), определенной на интервале (—8; 5). Определите количество целых

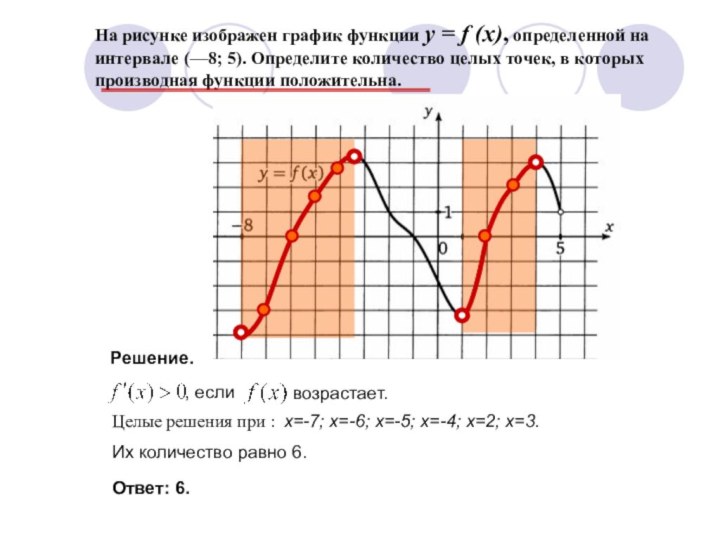
Решение.

Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.

Ответ: 6.

и только тогда, когда касательная к графику функции, проведенная

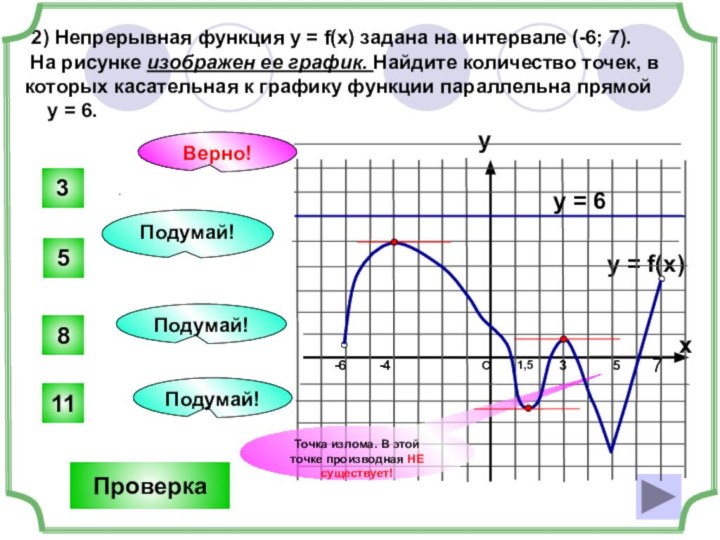
На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.

Теоретические сведения.

Решение.

если касательная, проведенная в эту точку имеет вид у = const.

Считаем количество точек пересечения графика функции с касательной.

Ответ: 7.

на интервале (-11; 3). Найдите количество точек, в которых

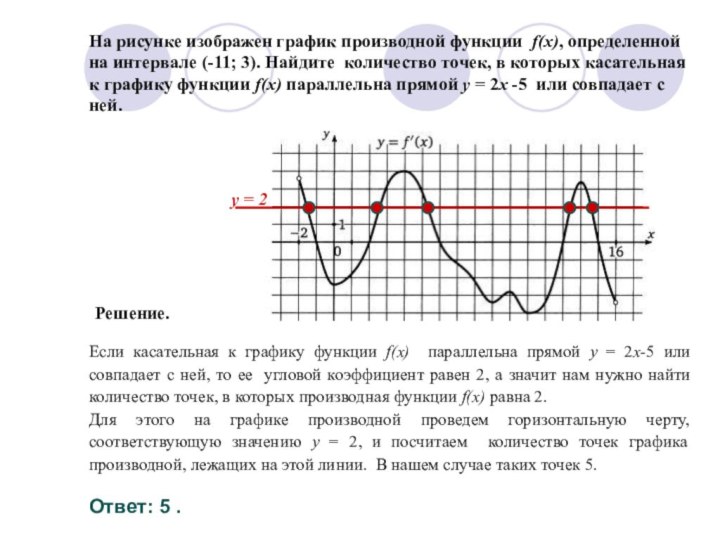
Если касательная к графику функции f(x) параллельна прямой y = 2x-5 или совпадает с ней, то ее угловой коэффициент равен 2, а значит нам нужно найти количество точек, в которых производная функции f(x) равна 2.
Для этого на графике производной проведем горизонтальную черту, соответствующую значению y = 2, и посчитаем количество точек графика производной, лежащих на этой линии. В нашем случае таких точек 5.

Решение.

y = 2

Ответ: 5 .

и касательная
к нему в точке с абсциссой х0.

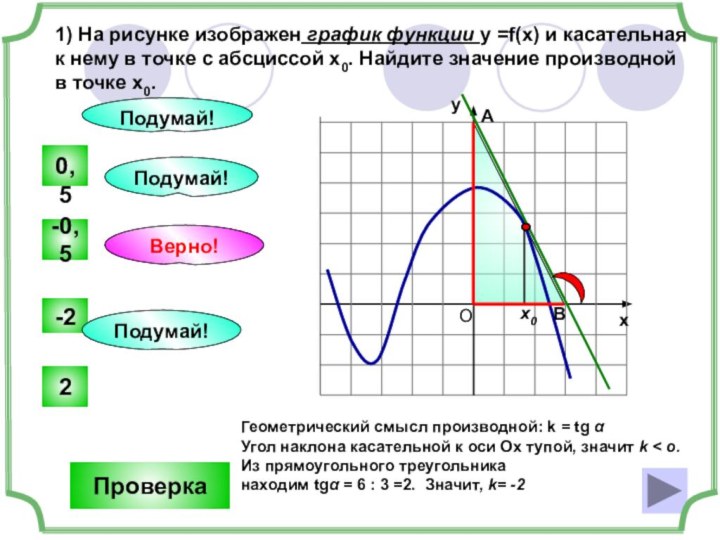
-2

-0,5

2

0,5

Подумай!

Подумай!

Верно!

Подумай!

х0

Геометрический смысл производной: k = tg α
Угол наклона касательной к оси Ох тупой, значит k < o.
Из прямоугольного треугольника
находим tgα = 6 : 3 =2. Значит, k= -2

Проверка

y

x

О

В

А

на интервале (-6; 7).
На рисунке изображен ее

Проверка

y = f(x)

y

x

3

Подумай!

Подумай!

Подумай!

Верно!

-6

7

.

Точка излома. В этой точке производная НЕ существует!

О

-4

3

5

1,5

/(x), заданной на промежутке (- 6; 8). Исследуйте функцию

2

1

4

5

Не верно!

Не верно!

Верно!

Не верно!

Проверка (2)

+

–

y = f /(x)

1 2 3 4 5 6 7

-7 -6 -5 -4 -3 -2 -1

4
3
2
1

-1
-2
-3
-4
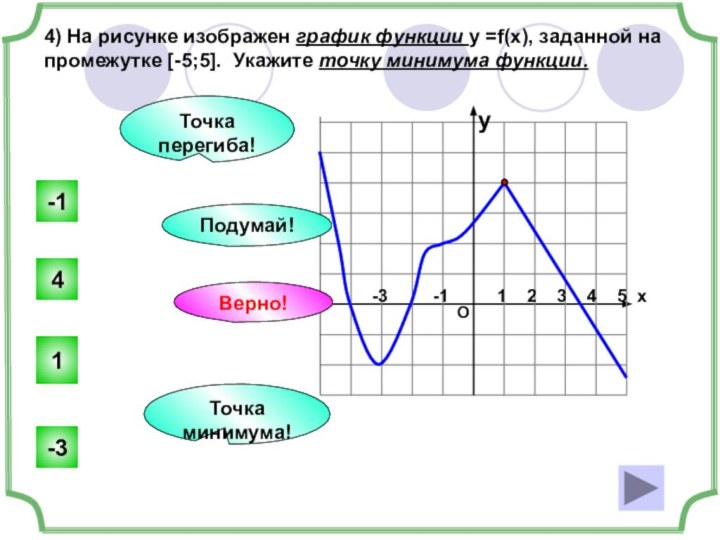
-5

y

x

+

О

5 х
4) На рисунке изображен график функции у =f(x),

1

4

-3

-1

Точка перегиба!

Точка минимума!

Верно!

Подумай!

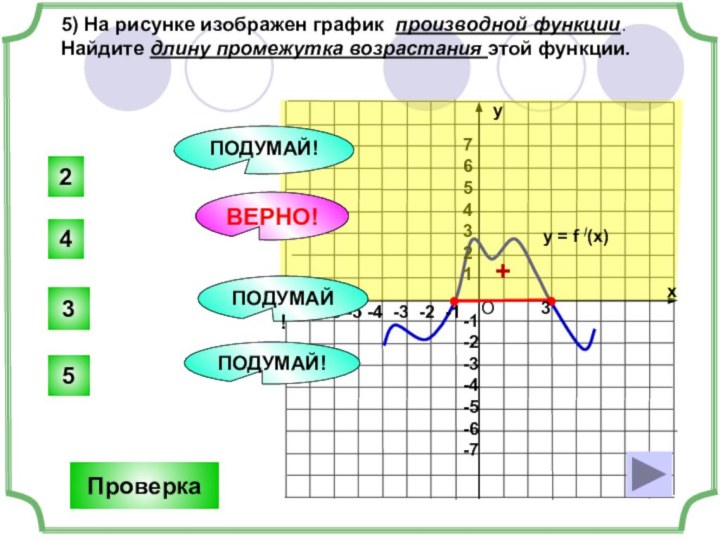
y

-3

-1

длину промежутка возрастания этой функции.
Проверка


О
-7 -6 -5 -4 -3

7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

4

2

3

5

ПОДУМАЙ!

+

ПОДУМАЙ!

ВЕРНО!

ПОДУМАЙ!

y

х

3

y = f /(x)

то чего мы не знаем, - бесконечно». Пьер