арифметической прогрессией, другая – геометрической:
-15; -12; -9;
-6; -3; 0;… d=3
32; 16; 8;
4; 2; 1;… q=1/2
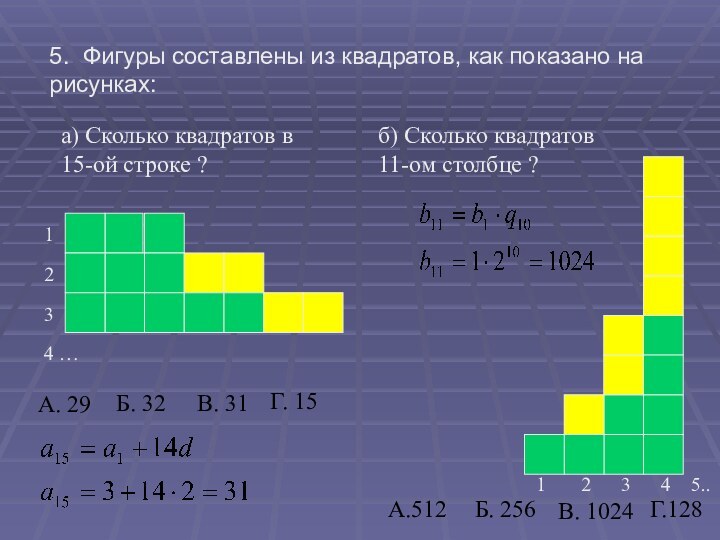
Продолжите каждую из этих прогрессий и назовите следующие три её члена.
2. Укажите формулу n- го члена арифметической прогрессии:
А. аn= -3n-15;
Б. an= 3n-15;
В. an= 3n-18;
Г. an= -3n+18;
А.
Б.
В.
Г.
4. Укажите формулу n-го члена геометрической прогрессии:
3.Является ли число 72 членом данной прогрессии?
72=3n-18
n=30,