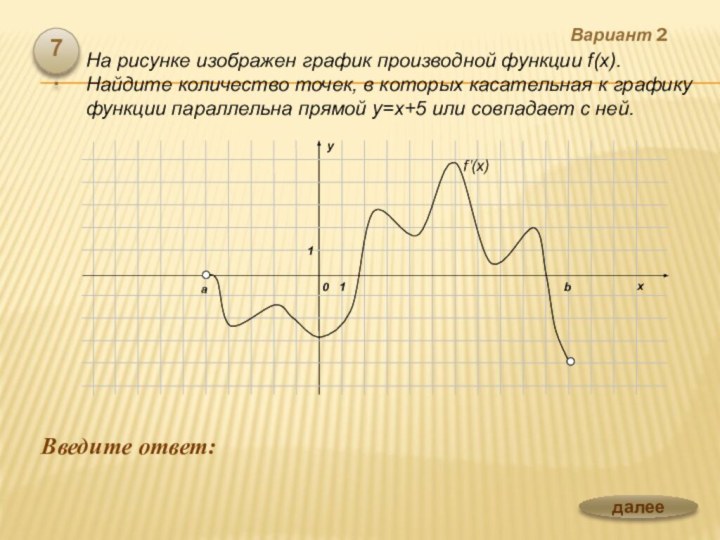
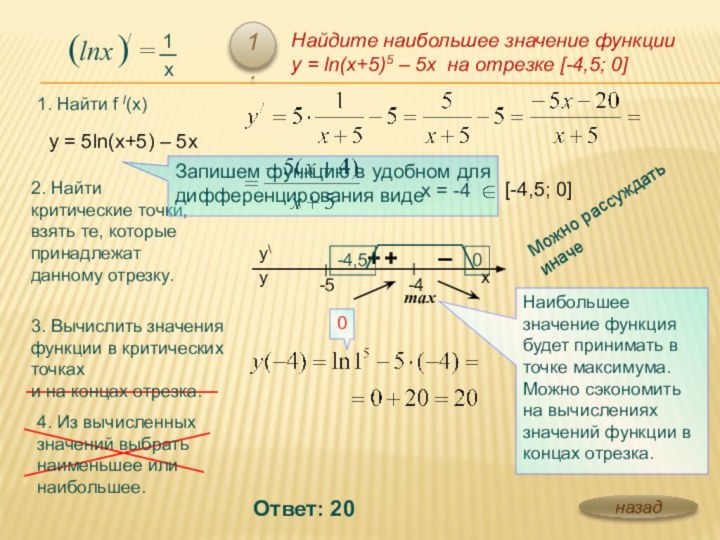
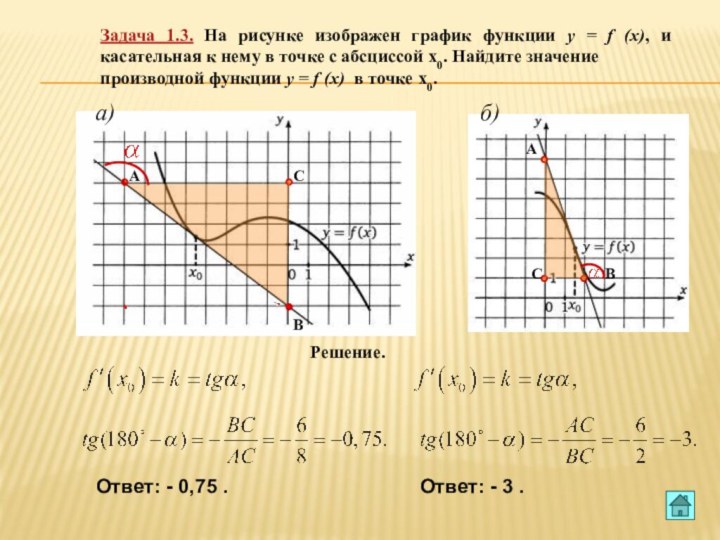
ее применение»
Цели:
Образовательные: рассмотреть применение производной в
заданиях
В-8, В-14 (ЕГЭ), вырабатывать у учащихся практические умения и навыки по применению производной.
Развивающие: способствовать дальнейшему развитию
математически грамотной речи, внимания, наблюдательности,
самоконтроля, исследовательских навыков учащихся,
математического и логического мышления, активизации
познавательской деятельности.
Воспитательные: воспитывать аккуратность,
дисциплинированность, способность самостоятельно принимать
решения.
Место урока в системе уроков по теме: обобщающий урок по
теме
«Производная и ее применение»
Тип урока: комбинированный
Формы урока: фронтальные, индивидуальные
Оборудование: компьютер, проектор, карточки с проверочной
работой, доска, мел.




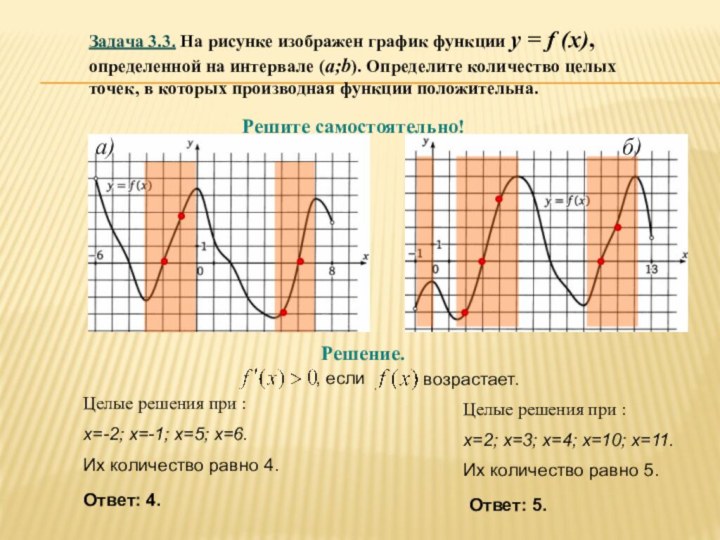
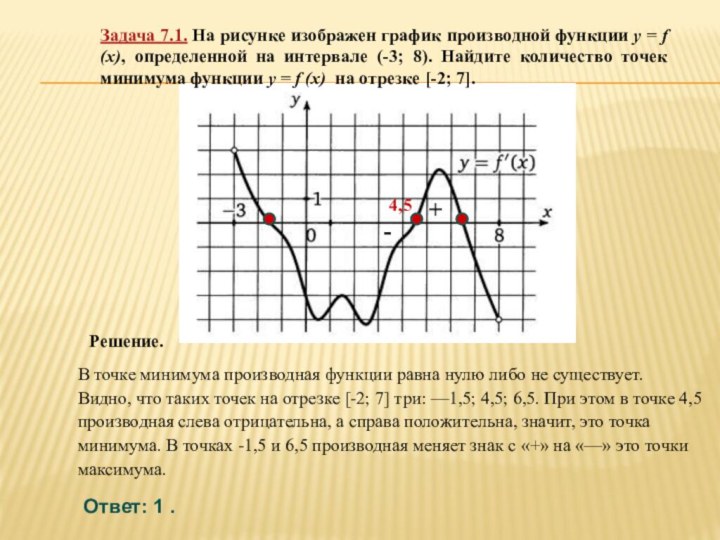


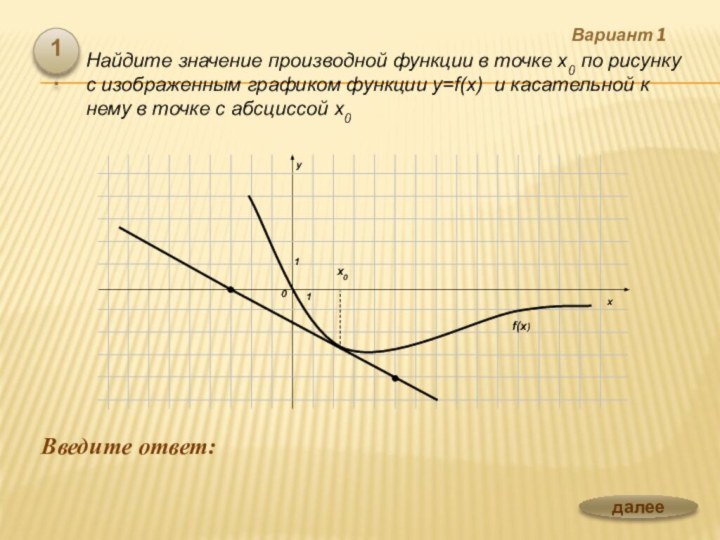
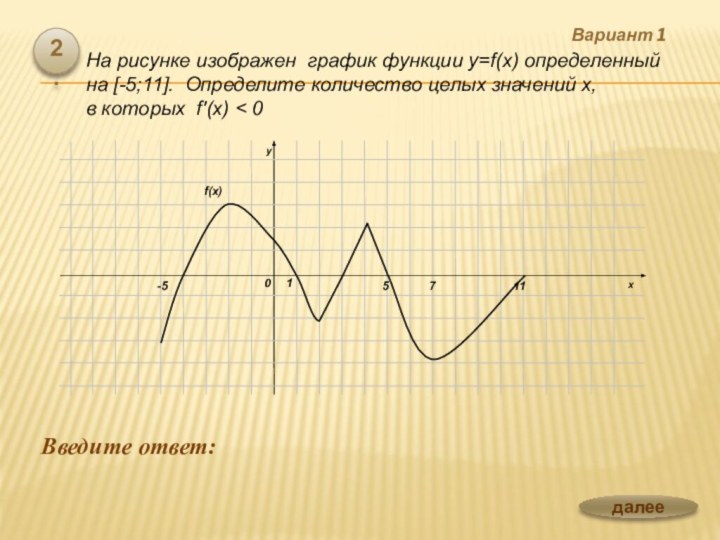
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 1 Введите ответ: 3.На рисунке изображен график функции y=f(x) на [а;b].](/img/tmb/6/563262/bddd1f23263fb08a3fba4e850cd73d93-720x.jpg)
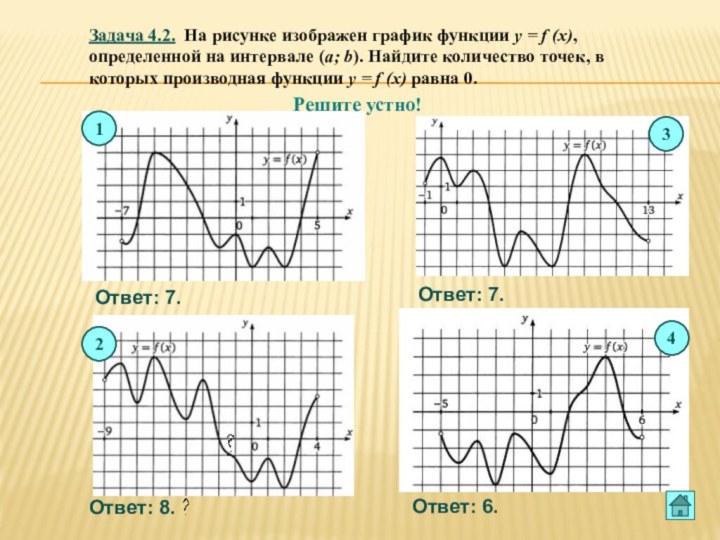
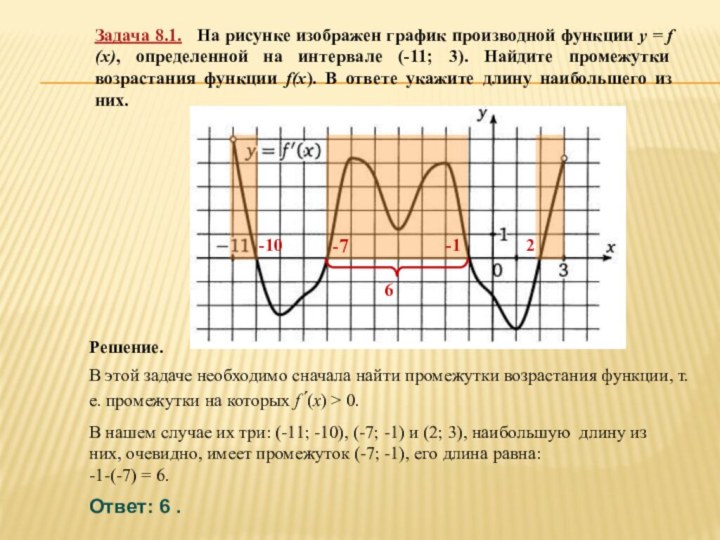
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 1 Введите ответ: 4.На рисунке изображен график функции y=f(x) на [-5;-3)U(-3;11].](/img/tmb/6/563262/58d5dcc020562696316519d655e15e28-720x.jpg)
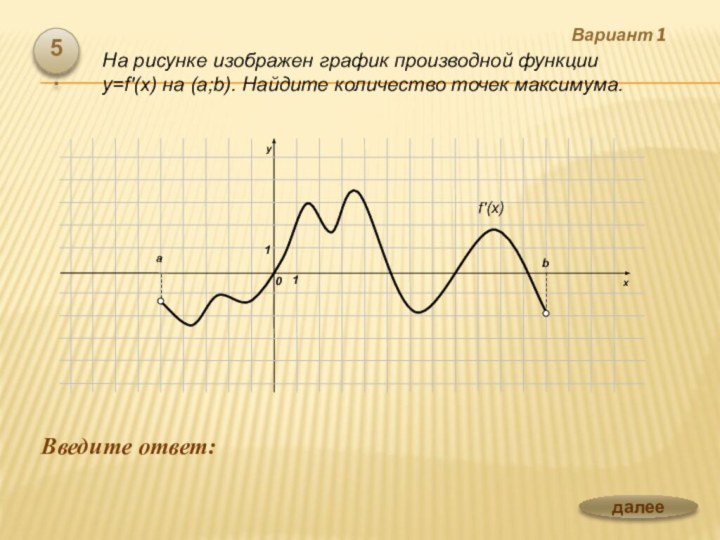
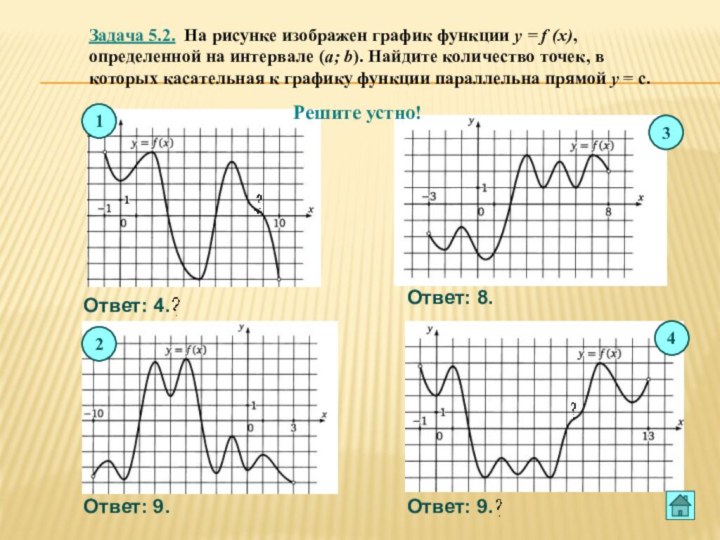
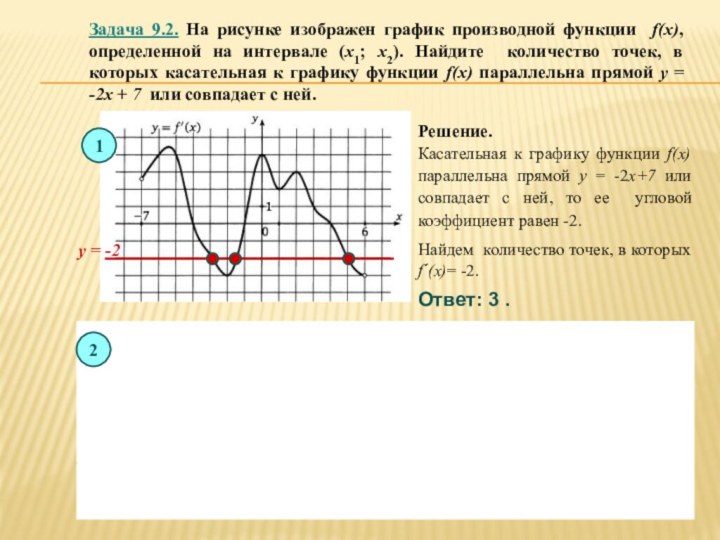
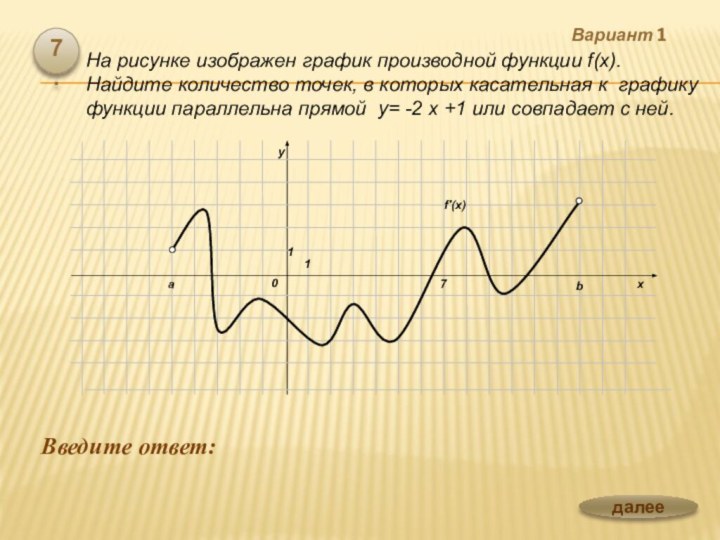
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 1 Введите ответ: 6.Функция определена на отрезке [-6;12]. На рисунке изображен](/img/tmb/6/563262/37ef7c143335b7744742059887f321e0-720x.jpg)

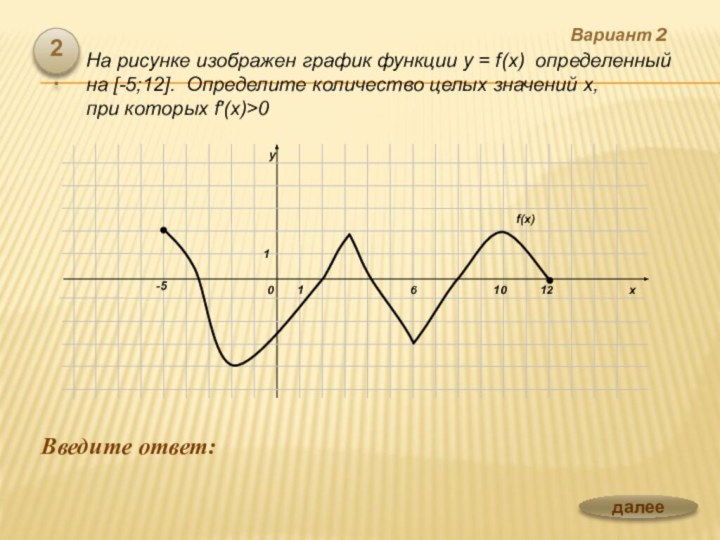
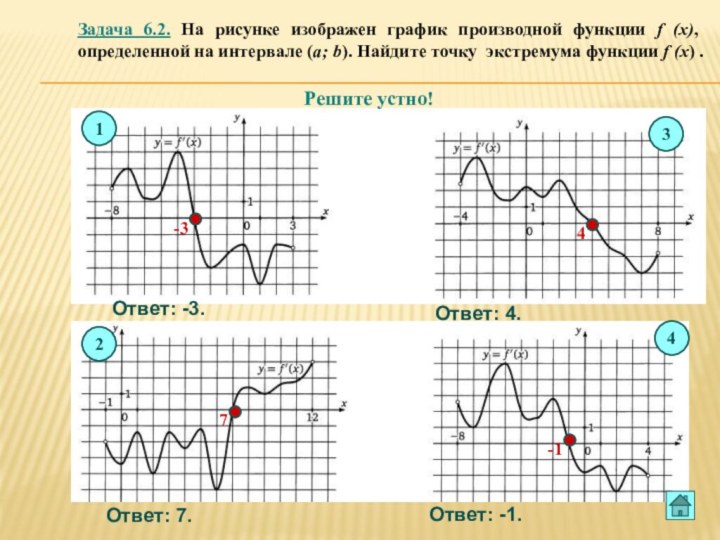
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 2 Введите ответ: 3.На рисунке изображен график функции y=f(x) на [а;b].](/img/tmb/6/563262/40567d85cb43138c5c93b50b026eaebf-720x.jpg)
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 2 Введите ответ: 4.На рисунке изображен график функции y=f(x) на [-5;-3)U(-3;11].](/img/tmb/6/563262/e64bbccc6336d024e1fa33d14e49c581-720x.jpg)
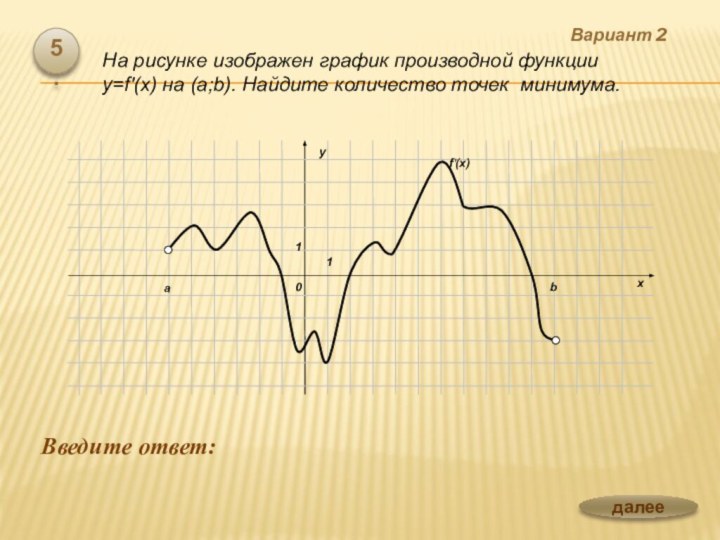
![Презентация по теме Производная и ее применение к уроку Алгебры 10 класс Вариант 2 Введите ответ: 6.Функция определена на отрезке [-5;12]. На рисунке изображен](/img/tmb/6/563262/9bd0d8deab5a00bae769d27f0677b3cd-720x.jpg)