Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Тригонометрические функции углового аргумента

Содержание

Цель урока: отработка навыка нахождения значений тригонометрических функций углового аргумента
Юркова И. А.,учитель математикиМБОУ «СОШ №8»г. Ханты-МансийскаУрок по теме «Значения тригонометрических функций углового аргумента»10-11 класс Цель урока: отработка навыка нахождения значений тригонометрических функций углового аргумента Задачи:1.обобщить и систематизировать учебный материал по теме «Значения тригонометрических функций Тригонометрические функции числового аргумента Опр.Косинусом угла А (соs A) называется абсцисса (х) точки, полученная поворотом точки 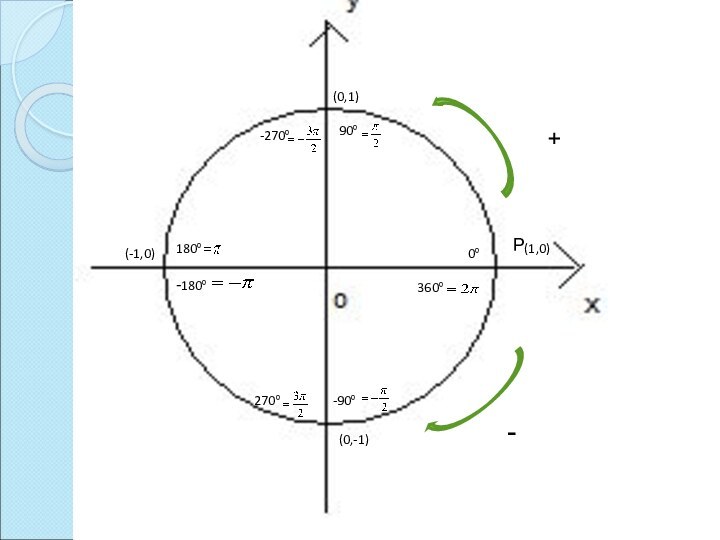Значения тригонометрических функций углов единичной окружности (0,1)(1,0)(0,-1)(-1,0)Р+90⁰180⁰270⁰360⁰0⁰--90⁰-180⁰-270⁰ Тригонометрические функции числового аргумента Значения тригонометрических функций основных углов ----- ------ ------222123 Тригонометрические функции числового аргумента Значения тригонометрических функций остальных углов таблицы 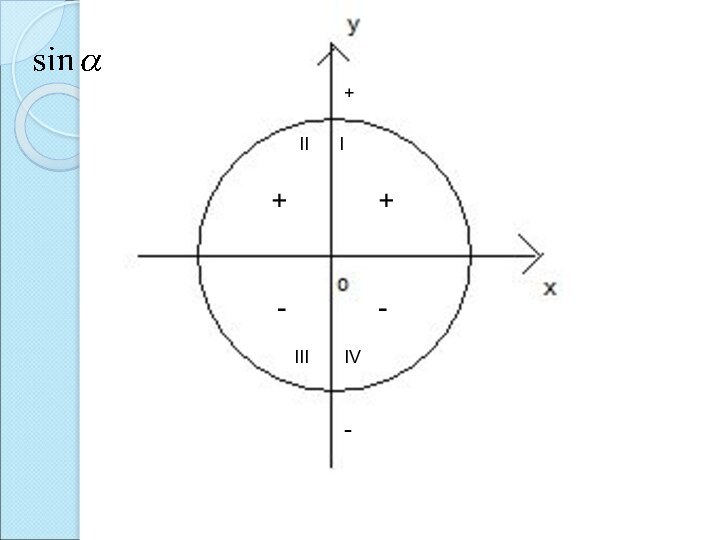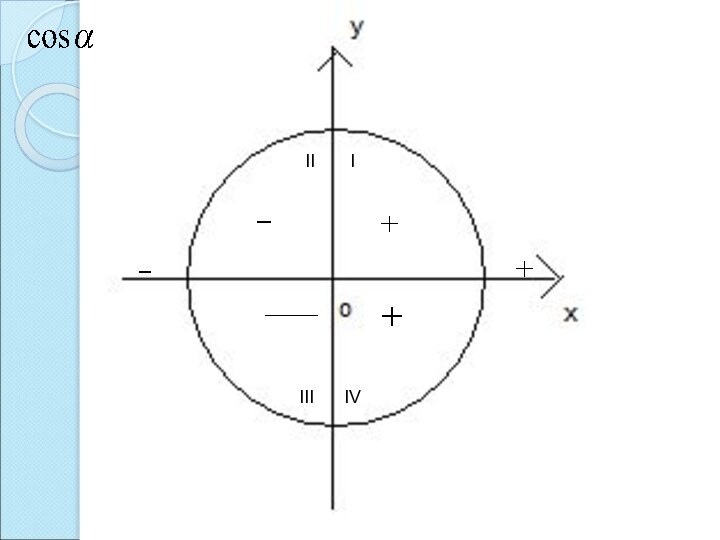Знаки тригонометрических функций в четвертях единичной окружности +-IIIIIIIV++-- IIIIIIIV IIIIIIIV+_+_ Формулы приведенияПравило 1Правило 2 Знак первоначальной функцииНазвание функции не меняетсяНазвание функции меняется на «кофункцию» Тригонометрические функции числового аргумента Задание Самостоятельная работа Вычислить:1. 2.3.4.5. Ответы1.2.3. _ 4. _5. -1 -
Слайды презентации

Слайд 2 Цель урока:
отработка навыка нахождения значений

Цель урока: отработка навыка нахождения значений тригонометрических функций углового аргумента

тригонометрических функций углового аргумента

Слайд 3 Задачи:
1.обобщить и систематизировать учебный материал по

Задачи:1.обобщить и систематизировать учебный материал по теме «Значения тригонометрических функций

теме «Значения тригонометрических функций углового аргумента»;
2.закрепить умение находить значения

тригонометрических функций углового аргумента;
3.отработать навык нахождения значений тригонометрических функций углового аргумента;
4.способствовать совершенствованию и развитию важнейших математических знаний и умений на основе полученных знаний по данной теме.

Слайд 4 Тригонометрические функции числового аргумента

Тригонометрические функции числового аргумента

Слайд 5 Опр.Косинусом угла А (соs A) называется абсцисса (х)

Опр.Косинусом угла А (соs A) называется абсцисса (х) точки, полученная поворотом

точки, полученная поворотом точки Р(1;0) вокруг начала координат на

угол А. Опр.Синусом угла А (sin A) называется ордината (у) точки, полученная поворотом точки Р(1;0) вокруг начала координат на угол А. Опр.Тангенсом угла А (tg A) называется отношение синуса угла А к косинусу угла А. Опр.Котангенсом угла А (ctg A) называется отношение косинуса угла А к синусу угла А.

Слайд 6 Значения тригонометрических функций углов единичной окружности

Значения тригонометрических функций углов единичной окружности

Слайд 7 (0,1)
(1,0)
(0,-1)
(-1,0)
Р

+
90⁰
180⁰
270⁰
360⁰
0⁰

-
-90⁰
-180⁰
-270⁰

(0,1)(1,0)(0,-1)(-1,0)Р+90⁰180⁰270⁰360⁰0⁰--90⁰-180⁰-270⁰

Слайд 8 Тригонометрические функции числового аргумента

Тригонометрические функции числового аргумента

Слайд 9 Значения тригонометрических функций основных углов

Значения тригонометрических функций основных углов

Слайд 10
-----
------
------
2
2
2
1
2
3

----- ------ ------222123

Слайд 11 Тригонометрические функции числового аргумента

Тригонометрические функции числового аргумента

Слайд 12 Значения тригонометрических функций остальных углов таблицы

Значения тригонометрических функций остальных углов таблицы

Слайд 13 Знаки тригонометрических функций в четвертях единичной окружности

Знаки тригонометрических функций в четвертях единичной окружности

Слайд 14 +
-
I
II
III
IV
+
+
-
-

+-IIIIIIIV++--

Слайд 15
I
II
III
IV

IIIIIIIV

Слайд 16 I
II
III
IV
+
_
+
_

IIIIIIIV+_+_

Слайд 17 Формулы приведения
Правило 1





Правило 2
Знак первоначальной функции
Название функции

Формулы приведенияПравило 1Правило 2 Знак первоначальной функцииНазвание функции не меняетсяНазвание функции меняется на «кофункцию»

не меняется
Название функции меняется на «кофункцию»

Слайд 18 Тригонометрические функции числового аргумента

Тригонометрические функции числового аргумента

Слайд 19

Задание

Задание





















Слайд 20 Самостоятельная работа
Вычислить:
1.

2.

3.

4.

5.












Самостоятельная работа Вычислить:1. 2.3.4.5.
  • Имя файла: trigonometricheskie-funktsii-uglovogo-argumenta.pptx
  • Количество просмотров: 163
  • Количество скачиваний: 0
- Предыдущая Музыка известных композиторов
Следующая - Фокина Л. П. Шаблон презентации - 1

Похожие презентации

Математическая логика Математическая логика 150
Презентация по математике Рационал өрнектерді көбейту Презентация по математике Рационал өрнектерді көбейту 186
Презентация к уроку Великаны и карлики Презентация к уроку Великаны и карлики 155
Презентация по алгебре на тему Степенная функция (Урок-мастерская) - 9 класс Презентация по алгебре на тему Степенная функция (Урок-мастерская) - 9 класс 296
Презентация по математике Арифметическая прогрессия (9 класс) Презентация по математике Арифметическая прогрессия (9 класс) 192
Первый урок по алгебре 8 класс Первый урок по алгебре 8 класс 257
Презентация Графическое решение уравнений Презентация Графическое решение уравнений 155
Урок геометрическая прогрессия Урок геометрическая прогрессия 199
Урок по алгебре в 7 классе Урок по алгебре в 7 классе 161
Презентация по математике на темуЛогарифмические уравнения (11класс) Презентация по математике на темуЛогарифмические уравнения (11класс) 139
График функции 7 класс График функции 7 класс 144
Решение задач по математике и экономике с помощью уравнений и неравенств Решение задач по математике и экономике с помощью уравнений и неравенств 207
Логические высказывания Логические высказывания 236
Презентация урока математики в 11 классе Исследование функции с помощью производной Презентация урока математики в 11 классе Исследование функции с помощью производной 166
Сложение и вычитание алгебраических дробей с разными знаменателями Сложение и вычитание алгебраических дробей с разными знаменателями 69
Решение уравнений, сводящихся к линейным Решение уравнений, сводящихся к линейным 248
Презентация к уроку алгебры по теме Преобразование выражений, содержащих квадратные корни Презентация к уроку алгебры по теме Преобразование выражений, содержащих квадратные корни 131
Формула корней квадратного уравнения Формула корней квадратного уравнения 179
Приведение Приведение 131
Презентация по математике на тему Неравенства Презентация по математике на тему Неравенства 157
Презентация по математике на тему Алгебра Презентация по математике на тему Алгебра 155
Логарифмы Логарифмы 163
Презентация по алгебре на тему: Рациональные дроби и их свойства Презентация по алгебре на тему: Рациональные дроби и их свойства 206
Применение производной в естествознании Применение производной в естествознании 156
Урок №23 Свойства степени с натуральным показателем Урок №23 Свойства степени с натуральным показателем 82
Арифметическая прогрессия Арифметическая прогрессия 158
Интеграл Интеграл 183
Презентация Обратные тригонометрические функции Презентация Обратные тригонометрические функции 161
Презентация по алгебре на тему Тригонометрические уравнения (10 класс) Презентация по алгебре на тему Тригонометрические уравнения (10 класс) 166
Натурал көрсеткішті дәреже және натурал көрсеткішті дәреженің қасиеттері тақырыбына презентация 7 сынып Натурал көрсеткішті дәреже және натурал көрсеткішті дәреженің қасиеттері тақырыбына презентация 7 сынып 294