- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Схема Горнера
Содержание
- 2. Cхема ГорнераСхема Горнера - это алгоритм вычисления
- 3. Горнер Вильямc Джордж (1786-22.9.1837)-английский математик. Родился в
- 4. СХЕМА ГОРНЕРА—способ деления многочлена n-й степенина линейный
- 5. Вычисления по схеме Горнера располагают в таблицу:Пример
- 6. Основным преимуществом этого метода является компактность записи
- 7. Пример2. Докажем, что многочлен Р(х)=х4-6х3+7х-392 делится на
- 8. Разложить на множители многочлен x3 – 5x2 – 2x + 16. Данный
- 9. Полученные числа 1, −3, −8 являются коэффициентами
- 10. Например, деление по схеме Горнера многочлена 2x3-4x2+5
- 12. Скачать презентацию
- 13. Похожие презентации
Cхема ГорнераСхема Горнера - это алгоритм вычисления значения многочлена при определенном значении переменной. Использование схемы Горнера значительно упрощает вычисления, а также помогает эффективно подбирать корни.











Слайд 3 Горнер Вильямc Джордж (1786-22.9.1837)-английский математик. Родился в Бристоле.
Учился и работал там же, затем в школах Бата.
Основные труды по алгебре. В 1819г. опубликовал способ приближенного вычисления вещественных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII в.) Именем Горнера названа схема деления многочлена на двучлен х-а.
Слайд 4
СХЕМА ГОРНЕРА
—способ деления многочлена n-й степени
на линейный двучлен
х — а,
основанный на том, что
коэффициенты неполного частногои остаток r связаны с коэффициентами делимого многочлена и с а формулами:
Слайд 5
Вычисления по схеме Горнера располагают в таблицу:
Пример 1.
Разделить
Неполное частное равно х3—х2+3х — 13
и остаток
равен 42=f(—3).Слайд 6 Основным преимуществом этого метода является компактность записи и
возможность быстрого деления многочлена на двучлен. По сути, схема
Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной. Ответ (разложение на множители) тут получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.
Слайд 7
Пример2.
Докажем, что многочлен Р(х)=х4-6х3+7х-392
делится на х-7,
и найдем частное от деления.
Решение.
Используя схему Горнера,
найдем Р(7):Отсюда получаем Р(7)=0, т.е. остаток при делении многочлена на х-7 равен нулю и, значит, многочлен Р(х) кратен (х-7).При этом числа во второй строке таблицы являются коэффициентами частного от деления Р(х) на
(х-7), поэтому
Р(х)=(х-7)(х3+х2+7х+56).
Слайд 8
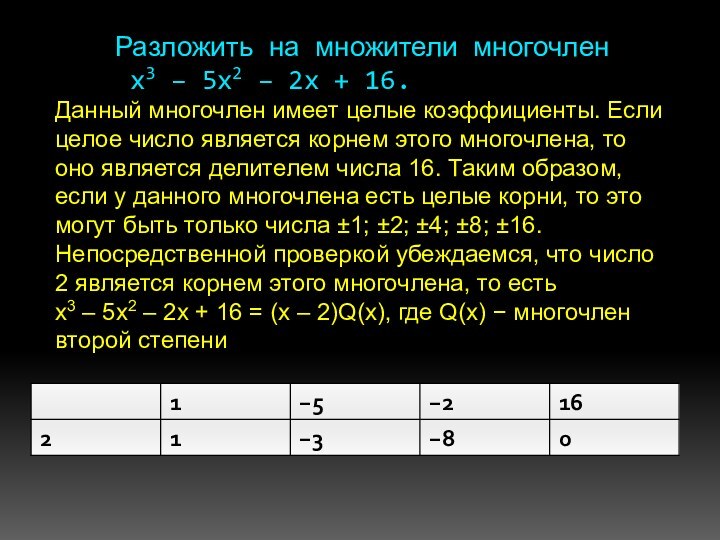
Разложить на множители многочлен
x3 – 5x2 – 2x + 16.
Данный многочлен имеет целые
коэффициенты. Если целое число является корнем этого многочлена, то
оно является делителем числа 16. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Непосредственной проверкой убеждаемся, что число 2 является корнем этого многочлена, то естьx3 – 5x2 – 2x + 16 = (x – 2)Q(x), где Q(x) − многочлен второй степени