Презентация на тему Линейная функция и ее график

переменными.
Рассмотреть линейную функцию и ее график.
Научить строить и читать

www.konspekturoka.ru

+ c = 0
3. Построим на координатной плоскости

4. Прямая – есть график уравнения.

Вспомним!

Внимание! Этот способ не удобен!

уравнения с двумя
переменными называется линейной функцией.
y – независимая

х – зависимая переменная

Графиком линейной функции y = kx + m есть прямая.

Теорема:

3, найти точку
пересечения с осью оу.
1. Составим таблицу

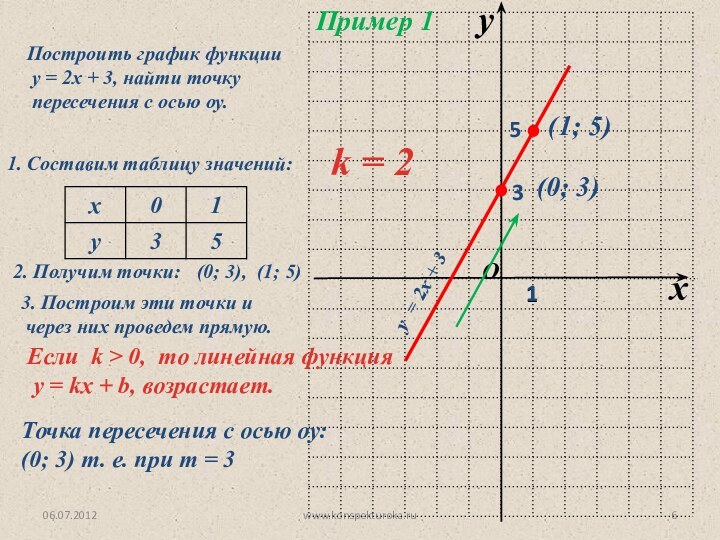
2. Получим точки:

(0; 3), (1; 5)

3. Построим эти точки и
через них проведем прямую.

(0; 3)

3

(1; 5)

у = 2х + 3

Если k > 0, то линейная функция
у = kx + b, возрастает.

k = 2

Точка пересечения с осью оу: (0; 3) т. е. при т = 3

+ 1 х  -3; 2
1. Составим

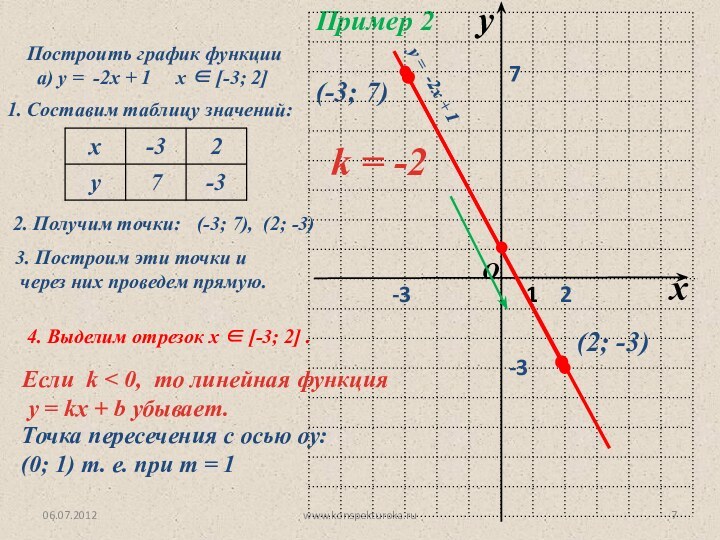
2. Получим точки:

(-3; 7), (2; -3)

3. Построим эти точки и
через них проведем прямую.

(-3; 7)

(2; -3)

4. Выделим отрезок х  -3; 2 .

Если k < 0, то линейная функция
у = kx + b убывает.

k = -2

у = -2х + 1

Точка пересечения с осью оу: (0; 1) т. е. при т = 1

+ 1 х  (-3; 2)
1. Составим

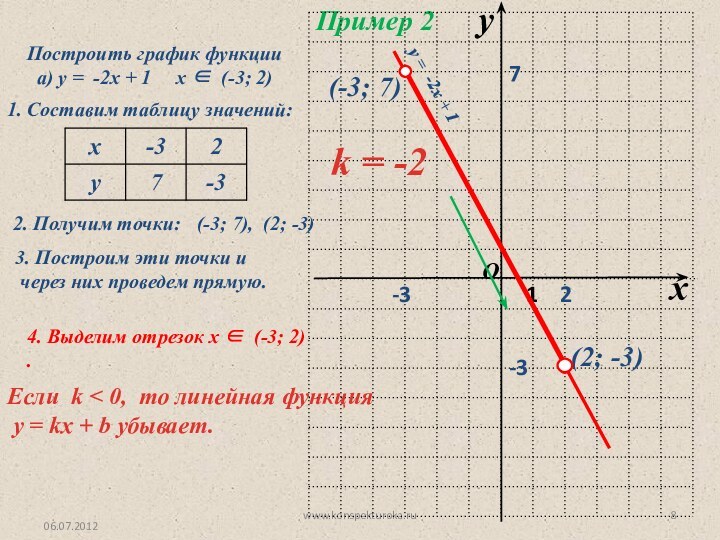
2. Получим точки:

(-3; 7), (2; -3)

3. Построим эти точки и
через них проведем прямую.

(-3; 7)

(2; -3)

4. Выделим отрезок х  (-3; 2) .

Если k < 0, то линейная функция
у = kx + b убывает.

k = -2

у = -2х + 1

(6; 7)
3. Построим эти точки и
через них проведем

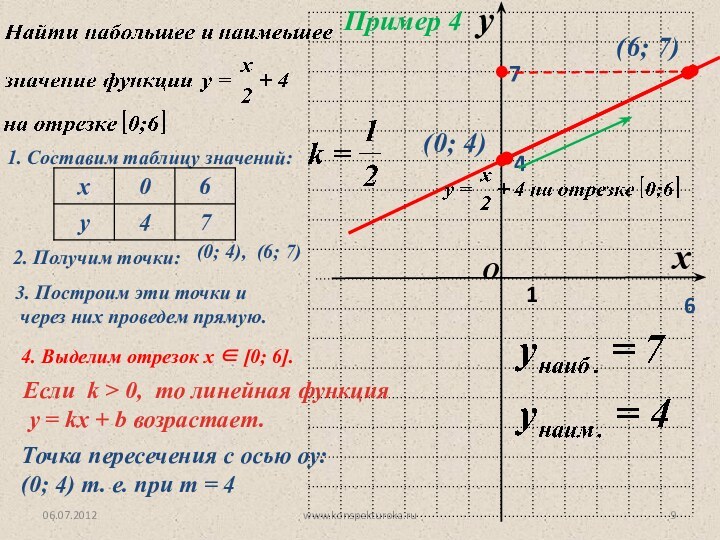
4

(0; 4)

4. Выделим отрезок х  0; 6.

(6; 7)

Если k > 0, то линейная функция
у = kx + b возрастает.

Точка пересечения с осью оу: (0; 4) т. е. при т = 4

если
большему значению аргумента соответствует
большее значение функции (двигаясь

Функция y = kx + m называется убывающей, если
большему значению аргумента соответствует
меньшее значение функции (двигаясь по графику
функции, мы опускаемся вниз).

kx + m
Если k < 0, то линейная

Если k > 0, то линейная функция
у = kx + b возрастает.

Если k = 0, то линейная функция
у = kx + b параллельна оси абсцисс
(или совпадает с ней).

любом значении аргумента
х значение функции равно одной

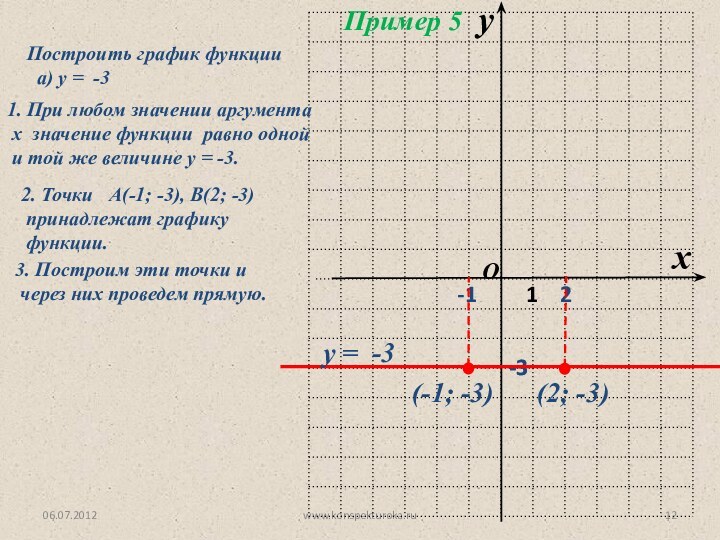
2. Точки А(-1; -3), В(2; -3)
принадлежат графику
функции.

3. Построим эти точки и
через них проведем прямую.

(-1; -3)

(2; -3)

у = -3

Пример 5