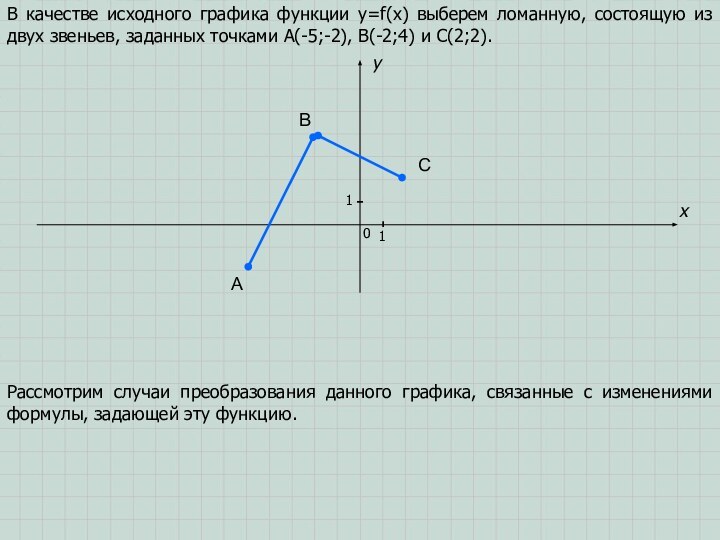
состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и
C(2;2).Рассмотрим случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

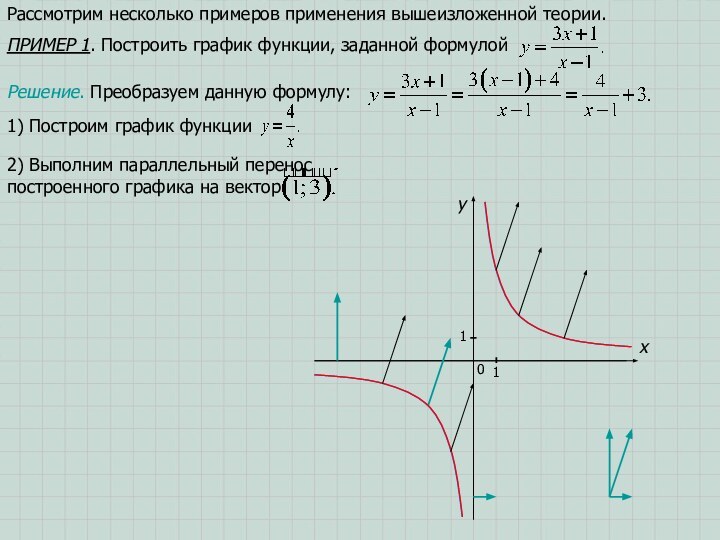
Рассмотрим случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию.
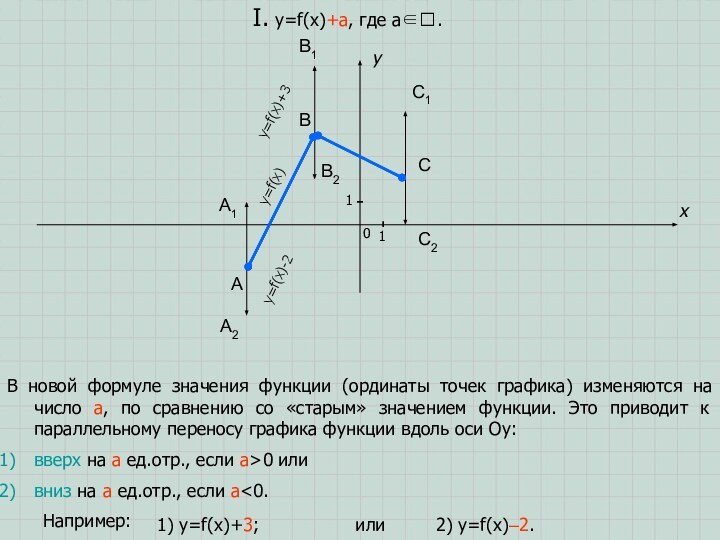
1) y=f(x)+3;
A1
B1
C1
y=f(x)
y=f(x)+3
или 2) y=f(x)–2.
A2
B2
C2
y=f(x)-2
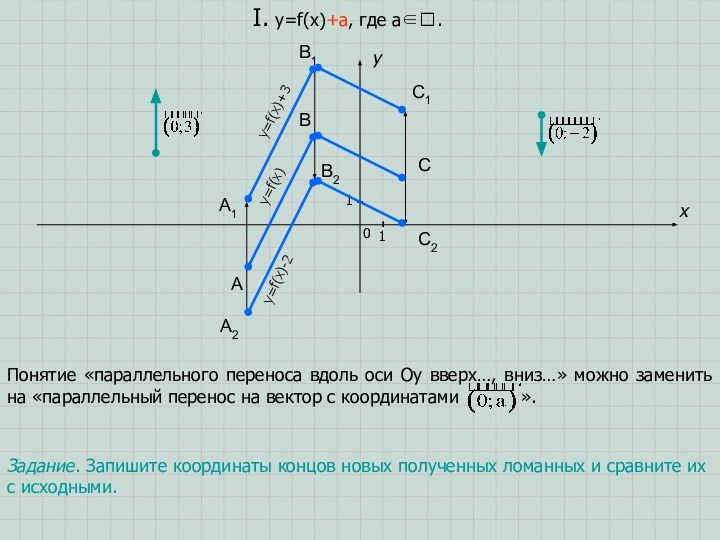
A1
B1
C1
y=f(x)
y=f(x)+3
A2
B2
C2
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
y=f(x)-2
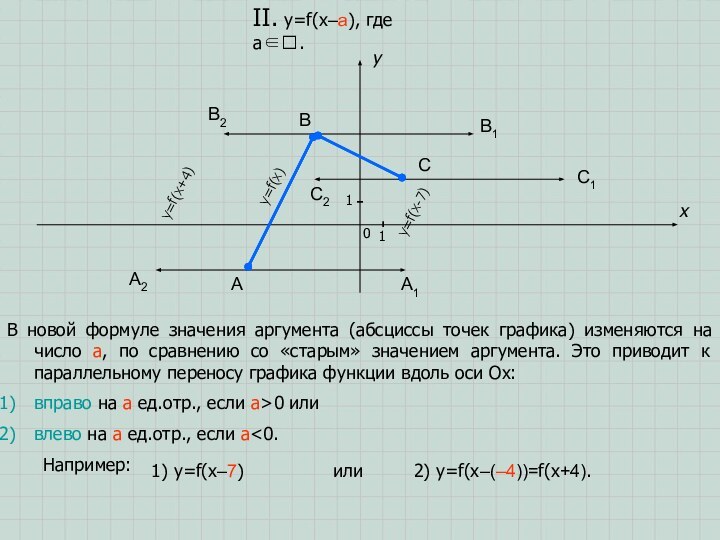
1) y=f(x–7)
y=f(x)
y=f(x-7)
A1
B1
C1
или 2) y=f(x–(–4))=f(x+4).
A2
B2
C2
y=f(x+4)
y=f(x)
y=f(x-7)
A1
B1
C1
A2
B2
C2
y=f(x+4)
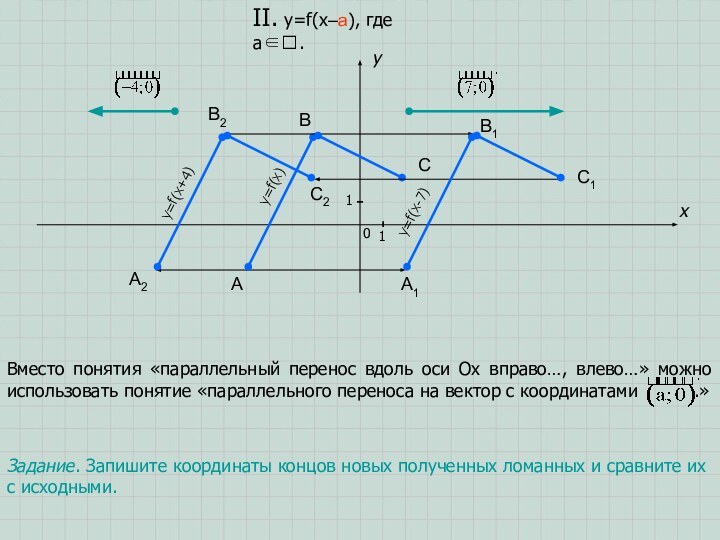
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=–f(x)
A1
B1
C1
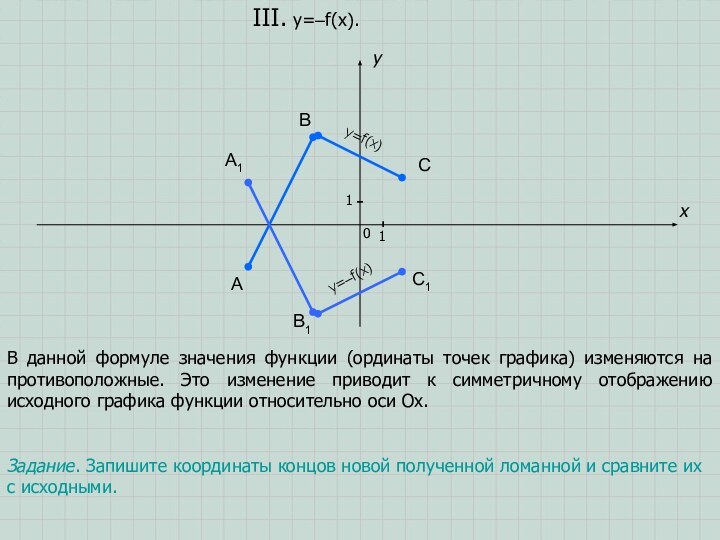
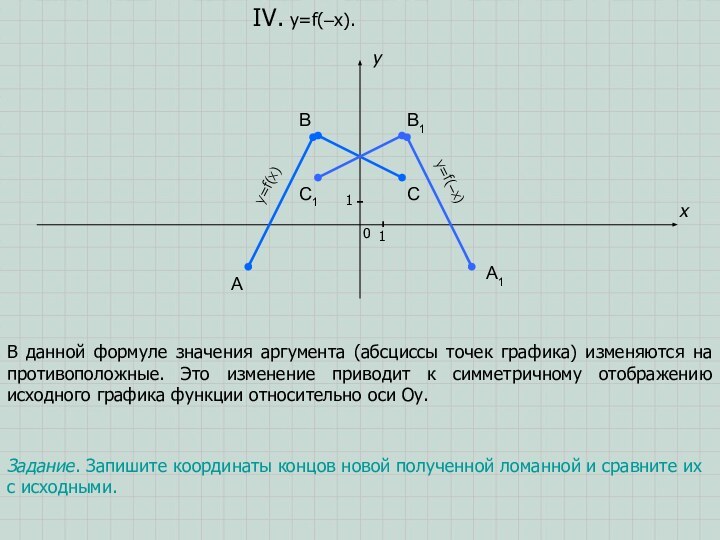
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=f(–x)
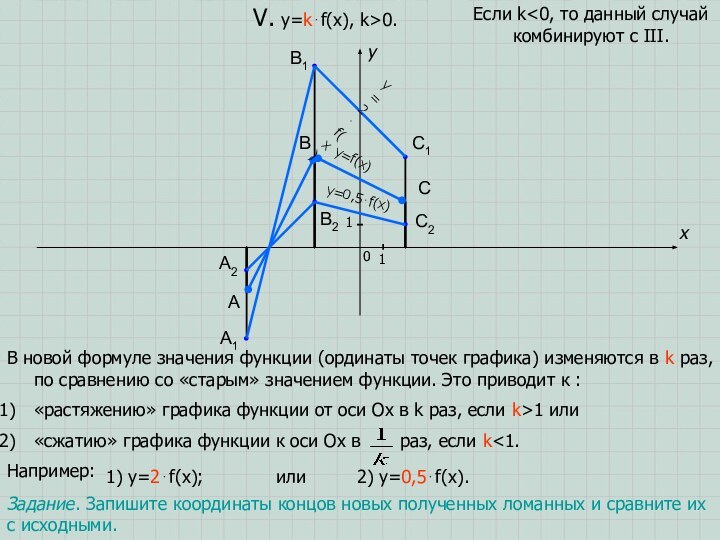
1) y=2⋅f(x);
или 2) y=0,5⋅f(x).
A1
B1
C1
y=f(x)
y=2⋅f(x)
A2
B2
C2
y=0,5⋅f(x)
Если k<0, то данный случай комбинируют с III.
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
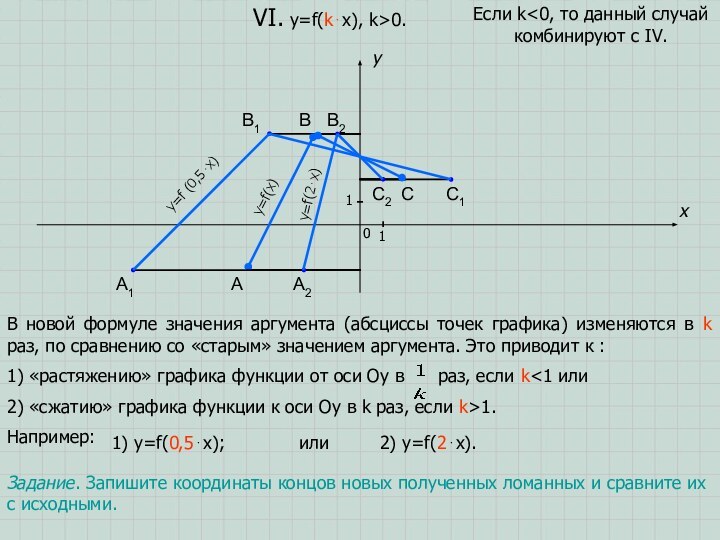
Если k<0, то данный случай комбинируют с IV.
1) y=f(0,5⋅x);
или 2) y=f(2⋅x).
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
A1
B1
C1
A2
B2
C2
y=f(x)
y=f (0,5⋅x)
y=f(2⋅x)
A1
M
Вспомните определение
модуля:
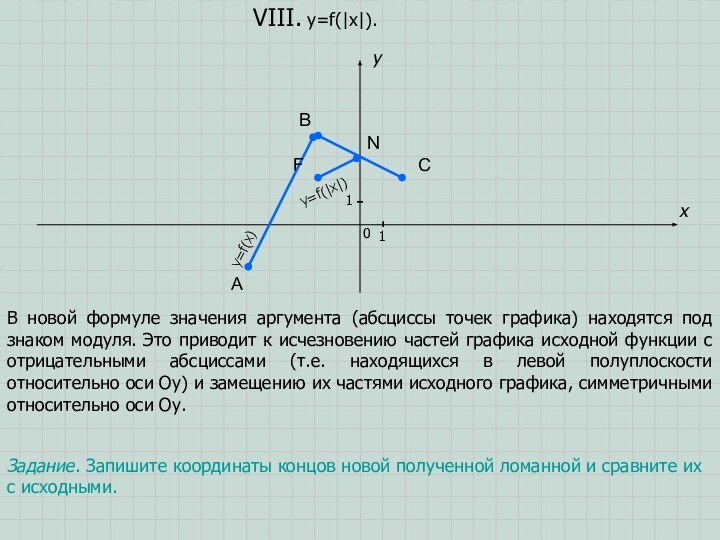
y=f(x)
y=|f(x)|
N
F
y=f(x)
y=f(|x|)