Презентация на тему Область определения числовой функции

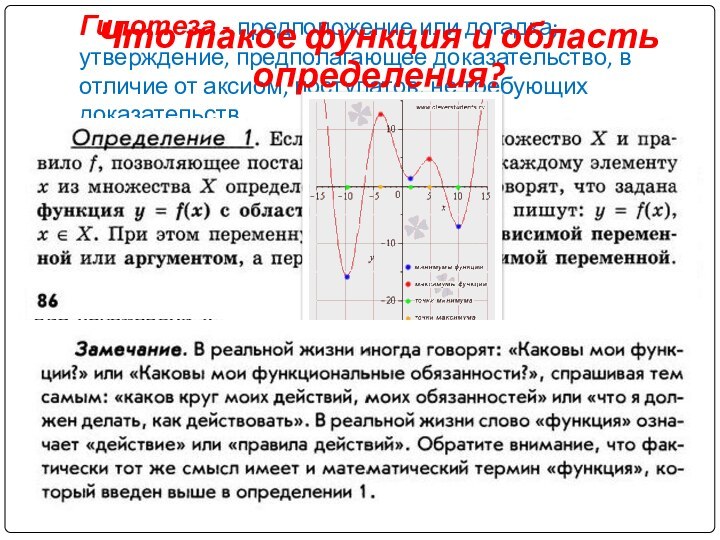
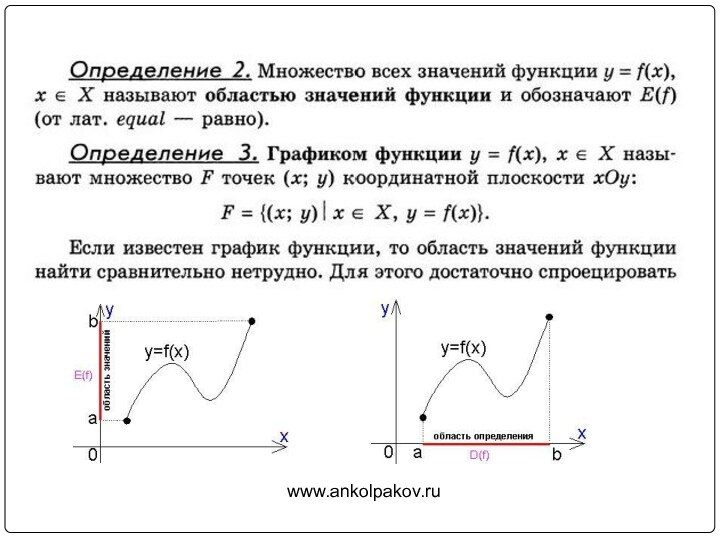
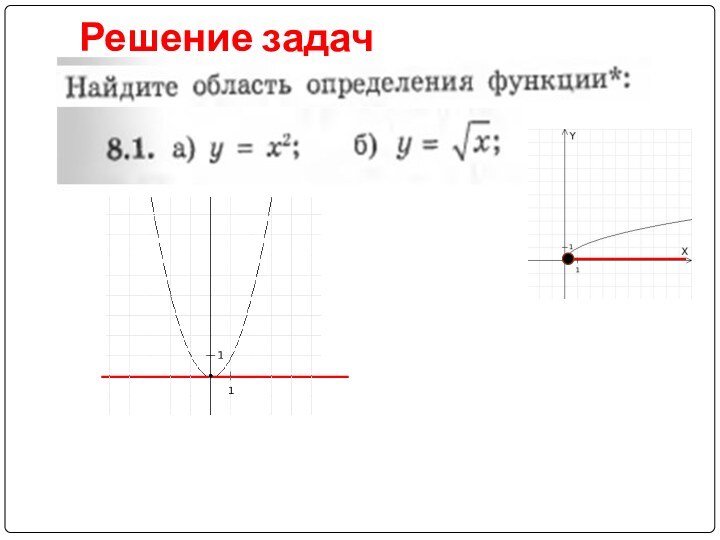
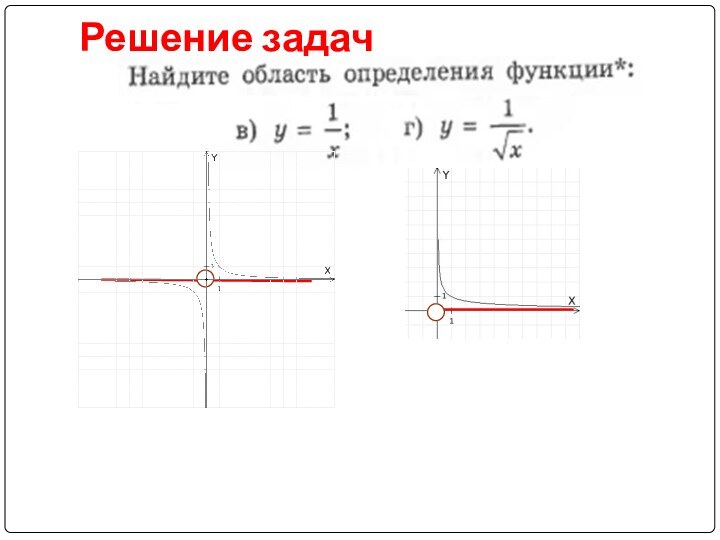
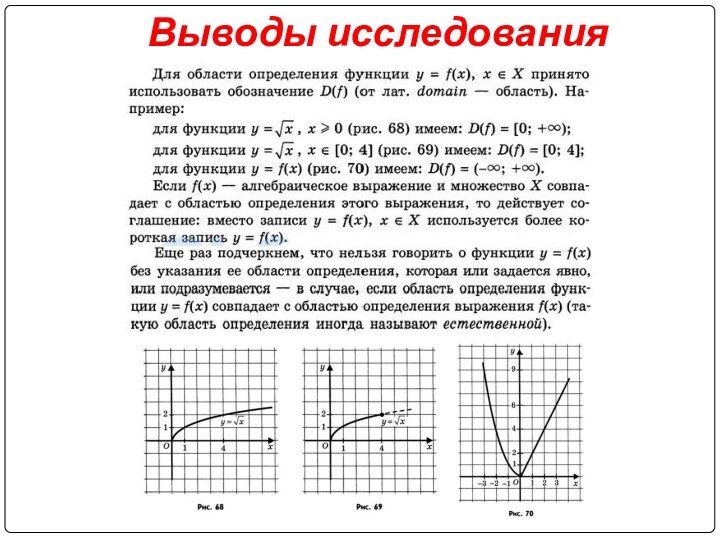
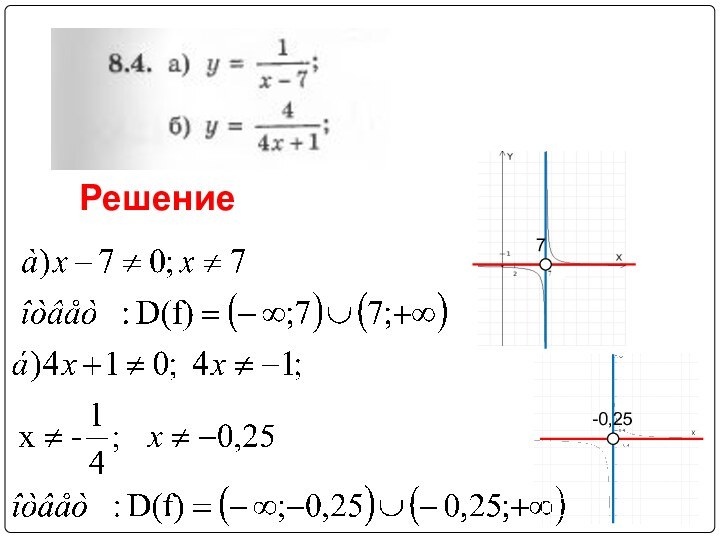
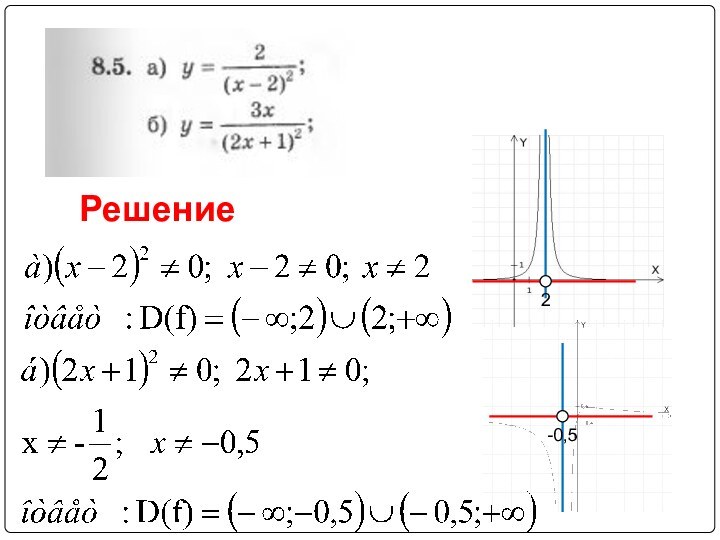
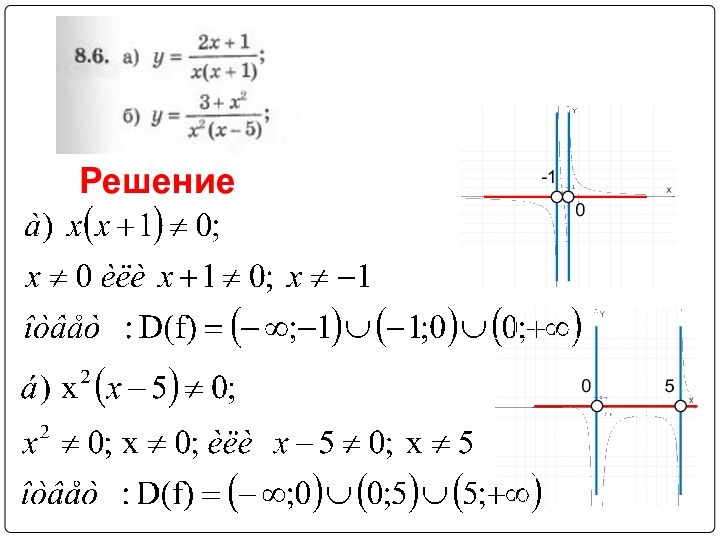
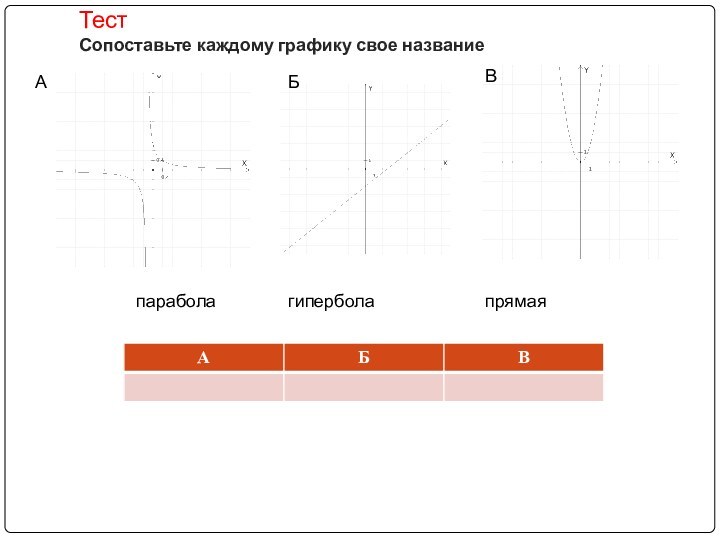
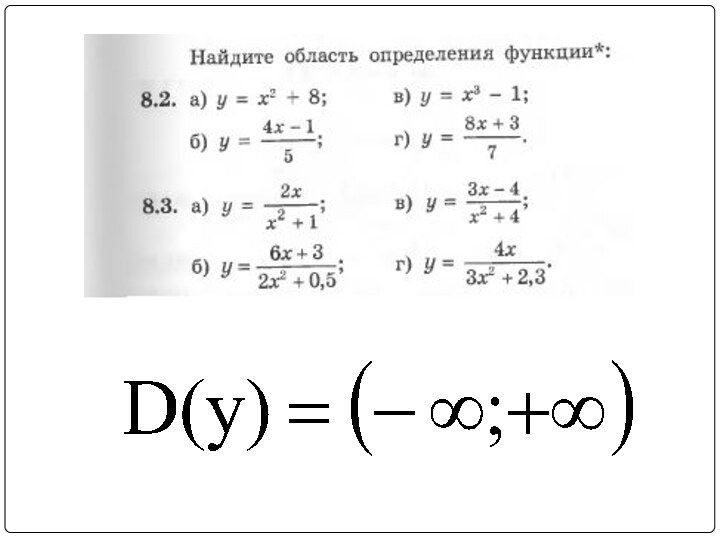, скобки использовались только в случае

многих аргументов, а также если аргумент представлял собой сложное выражение. Отголоском тех времён являются употребительные и сейчас записи   . Но постепенно использование скобок стало общим правилом, сейчас используются скобки при составлении выражений в программировании

Исаак
Ньютон

Го́тфрид Ви́льгельм Ле́йбниц

Жан Батист Жозеф Фурье

Карл Вейерштрасс

Леонард Эйлер

y=f(x) и ее области определении D(f)
ЧИСЛОВАЯ ФУНКЦИЯ.
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ.
Тема урока:

наблюдать, сравнивать, обобщать, делать выводы
Воспитание у учащихся целенаправленного отношения

к деятельности и применение в жизни

направлены вверх
Прямая, убывает
Гипербола, убывает
Парабола, ветви направлены вниз
Гипербола, возрастает
Прямая, возрастает

в отличие от аксиом, постулатов, не требующих доказательств
Что такое функция

и область определения?

функции, области определения, которые складывались постепенно в ходе изучения

алгебры в 7-м и 8-м классах
Мы сформулировали определения следующих понятий: функция, область определения функции, область значения функции
Рассмотрели различные способы задания функции: аналитический, графический, словесный
Ввели новое обозначение: D(f) для области определения функции

можно изобразить используя графический редактор на сайте http://www.reshmat.ru
Применение в

жизни функции