- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определение производной функции y=f(x) в точке
Содержание
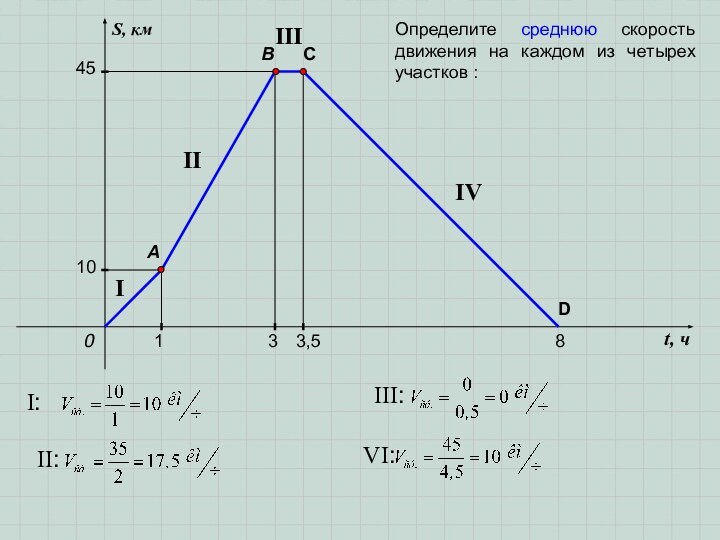
- 2. t, чS, км0AB11033,58C45DIIIIIIIVОпределите среднюю скорость движения на каждом из четырех участков :
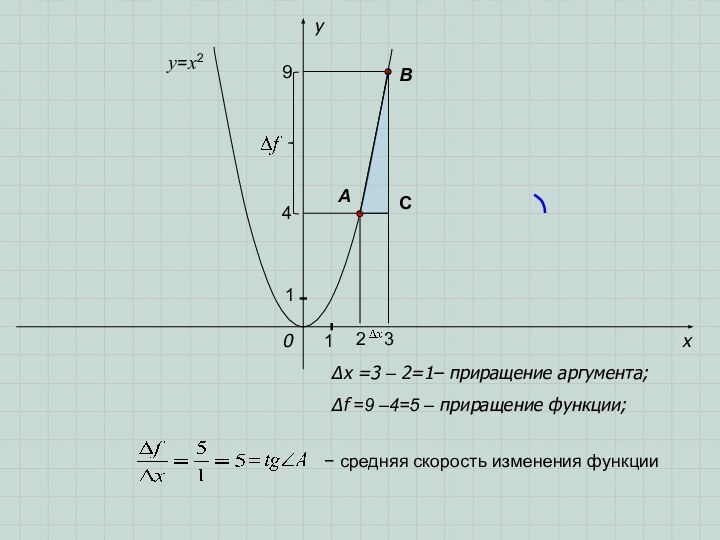
- 3. xy0AB∆f =9 –4=5 – приращение функции;∆x =3 – 2=1– приращение аргумента;y=x2119423C− средняя скорость изменения функции
- 4. t1t2t =t2–t1S1S2При Δt→0
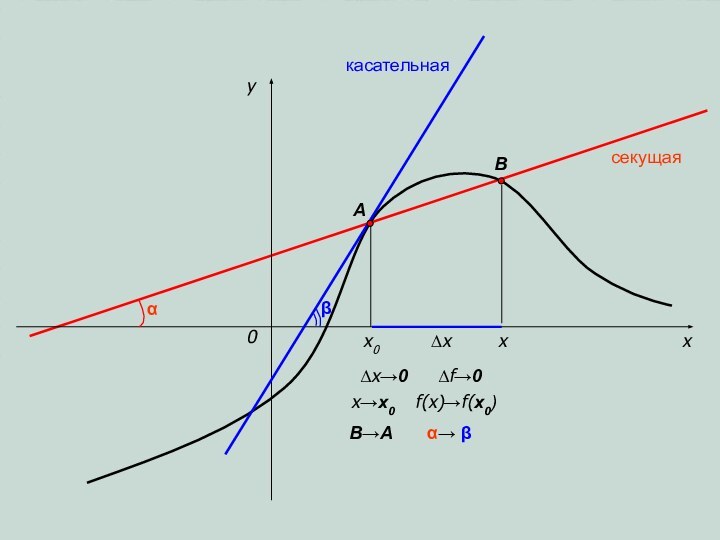
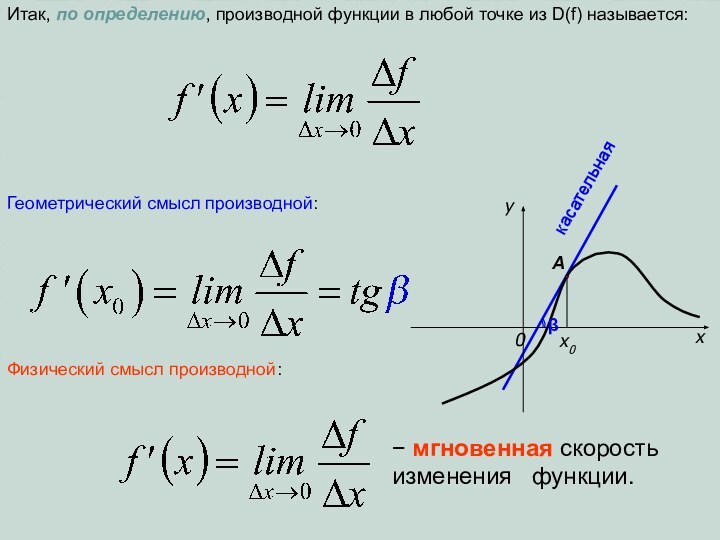
- 5. xy0x0x∆xсекущаякасательнаяПусть данная гладкая кривая – график функцииABαβf(x0)f(x0+∆x)∆f
- 6. xy0x0x∆x∆x→0x→x0секущаякасательнаяABB→Aβ∆f→0α→ βαf(x)→f(x0)
- 7. Скачать презентацию
- 8. Похожие презентации
t, чS, км0AB11033,58C45DIIIIIIIVОпределите среднюю скорость движения на каждом из четырех участков :



Слайд 2
t, ч
S, км
0
A
B
1
10
3
3,5
8
C
45
D
I
II
III
IV
Определите среднюю скорость движения на каждом
из четырех участков :
Слайд 3
x
y
0
A
B
∆f =9 –4=5 – приращение функции;
∆x =3 –
2=1– приращение аргумента;
y=x2
1
1
9
4
2
3
C
− средняя скорость изменения функции
Слайд 5
x
y
0
x0
x
∆x
секущая
касательная
Пусть данная гладкая кривая – график функции
A
B
α
β
f(x0)
f(x0+∆x)
∆f –
приращение функции
X0 – фиксированное значение аргумента
∆x – приращение аргумента
∆f
α
∆x
∆f
tg
α=