- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
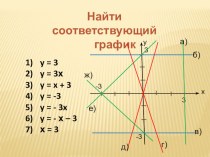
Презентация на тему Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №1
Содержание
- 2. Неравенство, содержащее переменную под знаком
- 3. Решение простейших логарифмических неравенств:a > 1x1 >
- 4. Решите неравенство:Решение традиционным способомОтвет: (2; 3)1)2)решений нет
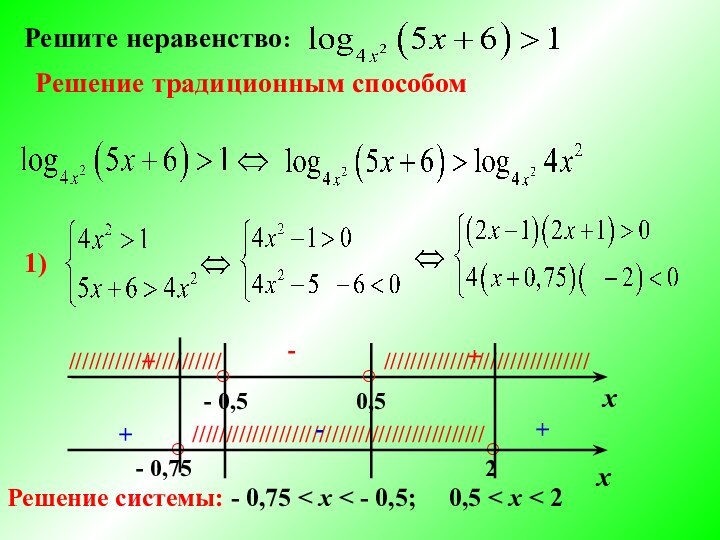
- 5. Решите неравенство:Решение традиционным способом1)х○○○○2- 0,75- 0,50,5х+-+//////////////////////////////////////////////////////////////////////////////////////////////////+-+Решение системы:
- 6. 2)х- 0,5○ 0,5○/////////////////0○///////////////////////////////////////////////////////////////////////////////- 0,75○//////////////////////2○Очевидно, что у системы
- 7. Интересное заключениео знакахдвух выражений
- 8. Доказать, чтовыражения log а b и (b
- 9. б)
- 10. Доказать, что при всех допустимых значениях переменной
- 11. а)Логарифмическая функция с основанием 2 возрастающая, тогда б)
- 12. Решение логарифмических неравенств с применением доказанного свойства
- 13. Алгоритм решения неравенства log h(x) f(x) >
- 14. Решите неравенство:1) ОДЗ:2) Переписываем неравенство в видеРешаем
- 15. Решите неравенство:1) ОДЗ:○○○○2- 0,75- 0,50,5х-+-+Ответ: - 0,75
- 16. Решите рассмотренным способом неравенстваОтвет: 3 <
- 17. Скачать презентацию
- 18. Похожие презентации















Слайд 2
Неравенство, содержащее переменную под знаком логарифма,
называется логарифмическим.
≠ 1 являются логарифмическим
Слайд 3
Решение простейших логарифмических неравенств:
a > 1
x1 > x2
> 0
a > 1
x2 > x1 > 0
0
a < 1x2 > x1 > 0
0 < a < 1
x1 > x2 > 0
Слайд 5
Решите неравенство:
Решение традиционным способом
1)
х
○
○
○
○
2
- 0,75
- 0,5
0,5
х
+
-
+
///////////////////////////////
///////////////////////
////////////////////////////////////////////
+
-
+
Решение системы: -
0,75 < x < - 0,5; 0,5
< x < 2
Слайд 6
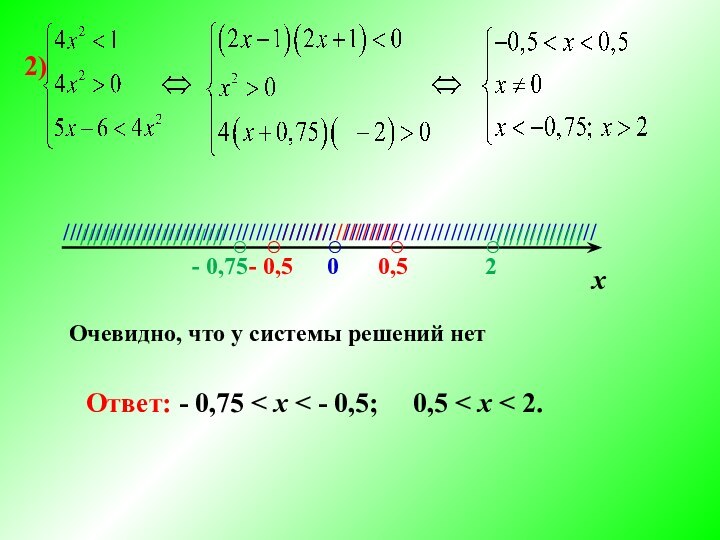
2)
х
- 0,5
○
0,5
○
/////////////////
0
○
//////////////////////////////////////
/////////////////////////////////////////
- 0,75
○
//////////////////////
2
○
Очевидно, что у системы решений
нет
Ответ: - 0,75 < x < - 0,5;
0,5 < x < 2./////////////
Слайд 8
Доказать, что
выражения log а b и (b –
1)(а – 1)
Доказательство.
1) Перейдём к основанию, например, 2
2)
Неравенство log а b > 0 перепишем в виде 3) Дробь положительна, если числитель и
знаменатель одинаковых знаков, тогда
одинаковых знаков.
Докажем, например, что log а b > 0
и (b – 1)(а – 1) > 0
а)
Логарифмическая функция с основанием 2 возрастающая, тогда
Слайд 10 Доказать, что при всех допустимых значениях переменной х
неравенство log h(x) f(x) > log h(x) g(x)
равносильно неравенству (f – g)(h – 1) > 0.
Доказательство.
1) Перейдём к основанию, например, 2
2) Неравенство log h f (х) > log h g(х) перепишем в виде
3) Дробь положительна, если числитель и знаменатель
одинаковых знаков, тогда
Слайд 13
Алгоритм решения неравенства log h(x) f(x) > log
h(x) g(x)
1) Находим область допустимых значений переменной (ОДЗ):
2)
Решаем неравенство (f(х) – g(х))(h(х) – 1) > 0. (Условимся далее две последние строки системы писать одной так: 0 < h(x) ≠ 0)
3) Для найденного решения учитываем ОДЗ.
4) Записываем ответ.
Слайд 14
Решите неравенство:
1) ОДЗ:
2) Переписываем неравенство в виде
Решаем неравенство
(х – (2х – 3))(2х – 3 – 1)
> 0;(х – 2х + 3)(2х – 4) > 0;
(– х + 3)2(х – 2) > 0;
– 2(х – 3)(х – 2) > 0
: (– 2);
(х – 3)(х – 2) < 0,
х
○
○
2
3
+
–
+
////////////////////////////////
1,5
○
////////////////////////////////////////////////////
ОДЗ
Ответ: (2; 3)
Слайд 15
Решите неравенство:
1) ОДЗ:
○
○
○
○
2
- 0,75
- 0,5
0,5
х
-
+
-
+
Ответ: - 0,75
x < - 0,5; 0,5 < x
< 22)
+
/////
//////////////
- 1,2
○
////////////////////////////////////////////////////
ОДЗ
○
0
Слайд 16
Решите рассмотренным способом неравенства
Ответ: 3 < x
< 4; x > 5.
Ответ: (- 3; -
1)Решения – в материалах следующего занятия