- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Остовное дерево
Содержание
- 2. Задача «Минимальное остовное дерево»Дано: Граф G, веса
- 3. Задача «Максимальный взвешенный лес»Дано: Граф G, веса
- 4. Эквивалентные задачиБудем говорить, что задача P линейно
- 5. ЭквивалентностьПредложение 4.1 Задача «Минимальное остовное дерево» и задача «Максимальный взвешенный лес» эквивалентны.
- 6. Доказательство(G,c) ― исходный пример задачи «Максимальный взвешенный
- 7. Условия оптимальности Теорема 4.2
- 8. (c)⇒(a)(с) Пусть T такое, что для любого
- 9. Алгоритм Краскала (1956)Input: Связный граф G, веса
- 10. Алгоритм Краскала (2)Теорема 4.3 Алгоритм Краскала находит оптимальное решение за O(mn).
- 11. Алгоритм Краскала (3)Теорема 4.4 Алгоритм Краскала можно реализовать за O(m log n).
- 12. Алгоритм Краскала (1956)Input: Связный граф G, веса
- 13. Как улучшить шаг 3Основная цель шага 3
- 14. ПроверкаПервоначально, B = (V(G), ø) и h(v)
- 15. Время работы шага 3Время работы пропорционально длине
- 16. Алгоритм Прима (1957)Input: Связный граф G, веса
- 17. Алгоритм Прима (2)Теорема 4.5 Алгоритм Прима находит решение за O(n2) элементарных операций.
- 18. Как реализовать шаг 2 While
- 19. Задача «Максимальный взвешенный ориентированный лес»Дано: Орграф G,
- 20. Задача «Минимальное остовное ориентированное дерево»Дано: Орграф G,
- 21. Задача «Минимальное остовное корневое ориентированное дерево»Дано: Орграф
- 22. Эквивалентность трех задачПредложение 4.6. Задачи
- 23. Ориентированный лес Орграф называется ориентированным лесом,
- 24. Ориентированный лес и циклыПредложение 4.7.
- 25. Доказательство леммыa1b1a2b2a3b3С ⊆ B0E(C)\ E(B)={(a1, b1),…, (ak,
- 26. Покажем, что в B есть bi-bi-1-путь для всех i.ai-1bi-1aibiai+1bi+1С ⊆ B0e∈E(B)E(B′):={(x,y)∈E(B)}\{e}U{(ai ,bi)}P∈BB′― не орлес.[bi-1 ai]∈B
- 27. Основная идеяНайти B0 ориентированный подграф G максимального
- 28. Алгоритм Эдмондса построения ориентированного леса максимального веса
- 29. Шаг 4zyxzvCС ⊆ Bie′α(e,C)For каждого ребра e
- 30. Шаг 6zvCe′∈ E(B)zyxС ⊆ Biα(e,C)eCevCyxС ⊆ Biα(e,C)eC
- 31. Алгоритм ЭдмондсаТеорема 4.9 Алгоритм Эдмондса находит оптимальное решение.
- 32. ДоказательствоПоследовательно применяя шаг 4 алгоритма, мы получили
- 33. Доказательство (2)Пусть B'i–1 ― произвольный орлес в
- 34. Шаг 4zyxzvCС ⊆ Bie′α(e,C)Set ci+1 (e′) := ci (e) – ci (α(e,C)) + ci (eC)eCe
- 35. ИндукцияПо индукции, B ― ориентированный лес наибольшего веса в Gi .ci(B) ≥ ci(B'i)
- 36. Шаг 6zvCe′∈ E(B)zyxС ⊆ Biα(e,C)eCevCyxС ⊆ Biα(e,C)eC
- 37. Упражнение 4.2Пусть (V,T1) и (V,T2) два дерева
- 38. Упражнение 4.3Дан граф G с произвольными весами
- 39. Скачать презентацию
- 40. Похожие презентации
Задача «Минимальное остовное дерево»Дано: Граф G, веса c: E(G) → R .Найти остовное дерево в G наименьшего веса или определить, что G ― несвязный.
























![Остовное дерево Покажем, что в B есть bi-bi-1-путь для всех i.ai-1bi-1aibiai+1bi+1С ⊆ B0e∈E(B)E(B′):={(x,y)∈E(B)}\{e}U{(ai ,bi)}P∈BB′― не орлес.[bi-1 ai]∈B](/img/tmb/11/1072594/a951dd9fd2c7f98f6180a5febc91689d-720x.jpg)











Слайд 2
Задача «Минимальное остовное дерево»
Дано: Граф G, веса c:
E(G) → R .
веса или определить, что G ― несвязный.
Слайд 3
Задача «Максимальный взвешенный лес»
Дано: Граф G, веса c:
E(G) → R .
Найти лес в G наибольшего
веса.
Слайд 4
Эквивалентные задачи
Будем говорить, что задача P линейно сводится
к задаче Q, если существуют функции f и g,
вычислимые за линейное время, такие что f преобразует частную задачу x из P в частную задачу y из Q, и g преобразует решение f (x) в решение x.Eсли P линейно сводится к Q и Q линейно сводится к P , то обе задачи называются эквивалентными.
Слайд 5
Эквивалентность
Предложение 4.1
Задача «Минимальное остовное дерево» и
задача «Максимальный взвешенный лес» эквивалентны.
Слайд 6
Доказательство
(G,c) ― исходный пример задачи «Максимальный взвешенный лес».
Удалим все ребра отрицательного веса.
Положим c'(e) = – c(e).
Добавим
минимальное множество ребер F, так чтобы полученный граф G' стал связным. (Веса можно взять любые.)Решим задачу «Минимальное остовное дерево» на примере (G',c').
Удалив из решения множество ребер F, получим решение исходной задачи.
(G,c) ― исходный пример задачи «Минимальное остовное дерево».
Положим c'(e) = K – c(e), где K = 1 + max e ∈ E(G) c(e).
Решение задачи «Максимальный взвешенный лес» на примере (G',c') дает решение задачи «Минимальное остовное дерево» на исходном примере.
Слайд 7
Условия оптимальности
Теорема 4.2
Пусть
(G ,c) ― пример задачи «Минимальное остовное дерево», и
пусть T ― остовное дерево в G. Тогда следующие условия эквивалентны:T ― оптимум.
Для любого e = {x, y}∈ E(G)\ E(T), все ребра из x-y-пути в T не дороже чем e.
Для любого e ∈ E(T), e ― ребро наименьшей стоимости из δ(V(C)), где C ― связная компонента на T– e.
Слайд 8
(c)⇒(a)
(с) Пусть T такое, что для любого e
∈ E(T), e ― ребро наименьшей стоимости из δ(V(C)),
где C ― связная компонента на T– e.Пусть T* оптимальное решение, такое что E(T) ∩ E(T*) максимально возможное. Покажем, что T = T*.
Пусть e = {x,y} ∈ E(T)\ E(T*).
Пусть C ― связная компонента на T– e.
T* + e содержит цикл D. Так как e ∈ E(D) ∩ δ(C), то существует f ≠ e, f ∈ E(D) ∩ δ(C).
Тогда (T* + e) – f является остовным деревом.
T* оптимум ⇒ c(e) ≥ c(f) и (с) ⇒ c(f) ≥ c(e).
c(f) = c(e) и (T* + e) – f является оптимальным остовным деревом.
Противоречие, так как в (T* + e) – f больше на одно общее ребро с T, чем в T* .
Слайд 9
Алгоритм Краскала (1956)
Input: Связный граф G, веса c:
E(G) → R .
Output: Остовное дерево T наименьшего веса.
Сортируем ребра так, что c(e1) ≤c(e2) ≤…≤c(em). Set T := (V(G), ∅).
For i := 1 to m do:
If T+ei не содержит цикла then T := T +ei.
Слайд 12
Алгоритм Краскала (1956)
Input: Связный граф G, веса c:
E(G) → R .
Output: Остовное дерево T наименьшего веса.
Сортируем ребра так, что c(e1) ≤c(e2) ≤…≤c(em). Set T := (V(G), ∅).
For i := 1 to m do:
If T+ei не содержит цикла then T := T +ei.
Слайд 13
Как улучшить шаг 3
Основная цель шага 3 проверить
не приведет ли добавление ребра ei = {v,w} к
образованию цикла.Это эквивалентно проверки лежат ли v и w в одной связной компоненте.
По ходу алгоритма будем строить дополнительный орлес B с V(B) = V(G), такой что связные компоненты B индуцированы на тех же вершинах, что и связные компоненты T.
Слайд 14
Проверка
Первоначально, B = (V(G), ø) и h(v) =
0, для всех v ∈V(G), где h(v) длина максимального
пути из v в B.3.1 Для ребра ei = {v,w} находим корни rv и rw ордеревьев в B, содержащих v и w.
3.2 Если rv = rw , то переходим к следующему ребру и идем на 3.1.
3.3 Если rv ≠ rw , то добавляем ei к T.
3.4. Если h(rv) ≥ h(rw), то добавляем дугу (rv, rw) к B, иначе добавляем дугу (rw, rv) к B.
Слайд 15
Время работы шага 3
Время работы пропорционально длине rv-v-пути
в B.
Покажем, что любое ордерево в B с корнем
r имеет по крайней мере 2h(r) вершин.Когда B = (V(G), ø) утверждение очевидно.
Пусть алгоритм добавляет дугу (x,y) в B. Получаем новое ордерево с корнем в x и числом вершин ≥ 2h(x) + 2h(y).
Если h(x) > h(y), то значение h(x) не меняется и утверждение справедливо.
Если h(x) = h(y), то значение h(x) увеличивается на 1. Число вершин в новом ордереве ≥ 2h(x) + 2h(y) =2h(x)+1.
h(r) ≤ log n, и трудоемкость шага 3 ≤ mlog n.
Слайд 16
Алгоритм Прима (1957)
Input: Связный граф G, веса c:
E(G) → R .
Output: Остовное дерево T минимального веса.
Выбрать v ∈ V(G). T := ({v}, ∅).While V(T) ≠V(G) do:
Выбрать ребро e ∈ δG(V(T)) минимальной стоимости. T := T +e.
Слайд 17
Алгоритм Прима (2)
Теорема 4.5
Алгоритм Прима находит решение
за O(n2) элементарных операций.
Слайд 18
Как реализовать шаг 2
While V(T)
≠V(G) do:
Выбрать ребро e ∈ δG(V(T))
минимальной стоимости. T := T +e.Для каждой вершины v∉V(T) будем хранить самое дешевое ребро (кандидата) из v в V(T).
Тогда выбор ребра минимальной стоимости и замена кандидатов может быть выполнена за O(n) элементарных операций.
Слайд 19
Задача «Максимальный взвешенный ориентированный лес»
Дано: Орграф G,
веса c: E(G) → R .
Найти ориентированный лес в G наибольшего веса.
Слайд 20
Задача «Минимальное остовное ориентированное дерево»
Дано: Орграф G,
веса c: E(G) → R .
Найти остовное ориентированное дерево в G наименьшего веса или определить, что оно не существует.
Слайд 21
Задача «Минимальное остовное корневое ориентированное дерево»
Дано: Орграф G,
вершина r ∊V(G),
веса c: E(G) → R .Найти остовное ориентированное дерево с корнем r в G наименьшего веса или определить, что оно не существует.
Слайд 22
Эквивалентность трех задач
Предложение 4.6.
Задачи «Максимальный
взвешенный ориентированный лес», «Минимальное остовное ориентированное дерево» и «Минимальное
остовное корневое ориентированное дерево» эквивалентны.Упражнение 4.1
Доказать предложение 4.6 .
Слайд 23
Ориентированный лес
Орграф называется ориентированным лесом, если
соответствующий ему граф является лесом и каждая вершина v
имеет не более одного входящего ребра.
Слайд 24
Ориентированный лес и циклы
Предложение 4.7.
Пусть
B ― орграф с
для всех x ∊ V(B). Тогда B имеет цикл тогда и только тогда, когда соответствующий ему граф имеет цикл.Лемма 4.8. (Karp [1972])
Пусть B0 ― подграф G максимального веса с
для всех v ∊ V(B0). Тогда существует оптимальный
ориентированный лес B в G такой, что для каждого
цикла C в B0, |E(C)\ E(B)| = 1.
Слайд 25
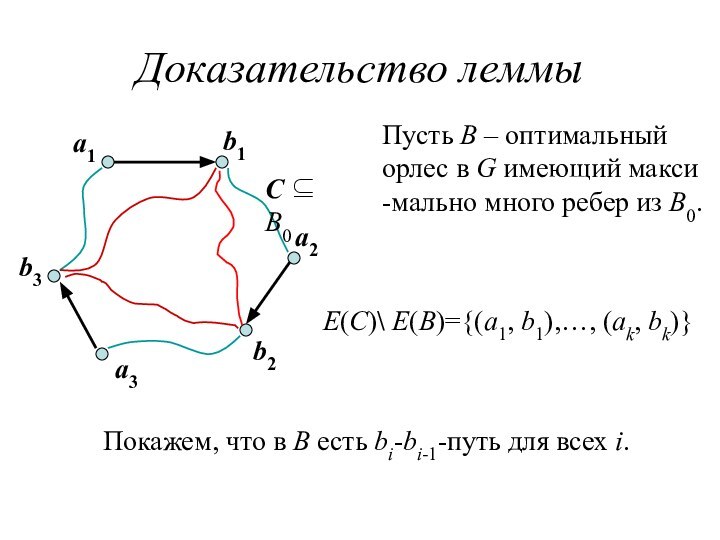
Доказательство леммы
a1
b1
a2
b2
a3
b3
С ⊆ B0
E(C)\ E(B)={(a1, b1),…, (ak, bk)}
Покажем,
что в B есть bi-bi-1-путь для всех i.
Пусть B
– оптимальныйорлес в G имеющий макси
-мально много ребер из B0.
Слайд 26 Покажем, что в B есть bi-bi-1-путь для всех
i.
ai-1
bi-1
ai
bi
ai+1
bi+1
С ⊆ B0
e∈E(B)
E(B′):={(x,y)∈E(B)}\{e}U{(ai ,bi)}
P∈B
B′― не орлес.
[bi-1 ai]∈B
Слайд 27
Основная идея
Найти B0 ориентированный подграф G максимального веса,
в котором в каждую вершину входит не больше одной
дуги.Стянуть каждый цикл в B0 в вершину.
Перераспредилить веса в новом графе G1, так чтобы любой оптимальный орлес в G1 соответствовал оптимальному орлесу в G.
Слайд 28
Алгоритм Эдмондса построения ориентированного леса максимального веса (1967)
Input:
орграф G, веса c: E(G) → R+ .
Output: орлес
максимального веса B of G.Set i :=0, G0 := G, и c0 := c.
Пусть Bi подграф G максимального веса с для всех v∊ Bi .
If Bi не содержит циклов then B := Bi и go to (5).
Построим (Gi+1, ci+1) из (Gi, ci): do для каждого цикла C из Bi . Стянем C к одной вершине vC в Gi+1. For каждого ребра e = ( z, y) ∈E(Gi) с z∉V(C), y∈V(C) do: Set ci+1 (e′) := ci (e) – ci (α(e,C)) + ci (eC) и Φ(e′) :=e,
где e′ := ( z, vC), α(e,C)=(x,y) ∈E(C), и eC самое дешевое ребро C.
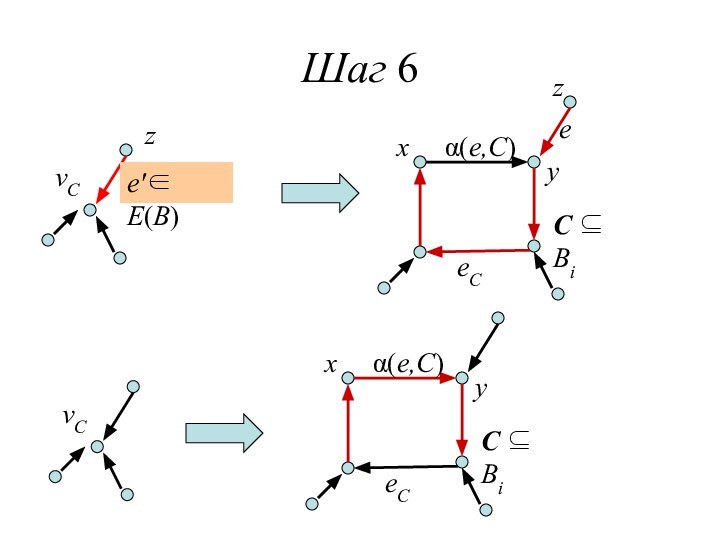
If i = 0 then stop.
For каждого цикла C из Bi-1 do:
If есть ребро e′ = ( z, vC) ∈ E(B)
then E(B) := (E(B)\{e′ }) ⋃Φ(e′) ⋃(E(C)\{α(Φ(e′),C)})
else E(B) := E(B) ⋃(E(C)\{eC}).
Set V(B) := V(Gi-1), i := i–1 и go to (5).
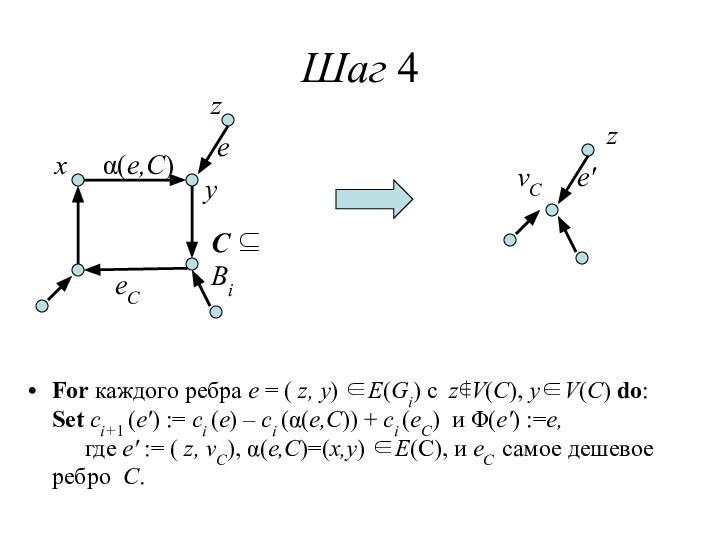
Слайд 29
Шаг 4
z
y
x
z
vC
С ⊆ Bi
e′
α(e,C)
For каждого ребра e =
( z, y) ∈E(Gi) с z∉V(C), y∈V(C) do:
Set ci+1 (e′) := ci (e) – ci (α(e,C)) + ci (eC) и Φ(e′) :=e,где e′ := ( z, vC), α(e,C)=(x,y) ∈E(C), и eC самое дешевое ребро C.
eC
e
Слайд 32
Доказательство
Последовательно применяя шаг 4 алгоритма, мы получили последовательность
(Gi, ci), i = 0,…, k.
Ясно, что полученный на
последнем применении шага 4 орлес B является оптимальным для (Gk, ck).Покажем, что на шаге 6 мы последовательно строим оптимальные решения для (Gi, ci), i = k–1,…,0.
Мы хотим показать, что шаг 6 переводит ориентированный лес наибольшего веса B для Gi в ориентированный лес наибольшего веса B* для Gi–1.
Слайд 33
Доказательство (2)
Пусть B'i–1 ― произвольный орлес в Gi–1,
такой что |E(C)\ E(B'i–1)| = 1 для любого
C из Bi–1.Пусть B'i получается из B'i–1 стягиванием циклов в Bi–1.
Тогда B'i орлес в Gi.