Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Последовательности

Содержание

Продолжи ряд1, 2, 3, 4, 5, 6 12, 10, 8, 6, 4 6, 9, 12, 15, 18, 21 2, 4, 8, 16, 32 1, 4, 16
Последовательности2011Васильева Е.Е. Продолжи ряд1, 2, 3, 4, 5, 6 12, 10, 8, 6, 4 Последовательности составляют такие элементы природы, которые можно пронумеровать Дни неделиКлассыВшколеДома наулице Квартиры вдоме Номерасчетов вбанкеНазвание месяцев Найдите закономерности и покажите их стрелками В порядке возрастания положительные нечетные числаВ Определение Функцию y=f(x), определенную на множестве натуральных чисел xϵN (или Числа y1, y2, …, yn называют членами последовательности, Члены последовательности обозначаются так: a1a2a3a4…anПервыйчленВторойчленТретийчленЧетвертыйчленn-членпоследовательности Задать числовую последовательность— это значит указать, как отыскивается тот или иной ее Способы описания последовательности Последовательности можно задавать различными способами, среди которых особенно Формула1. Последовательность задана аналитически, если задана формула ее n-го члена: yn = Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких РекурентныйРекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить Пример рекуррентного заданияПример 1. y1 = 3; yn = yn–1 + 4, Графиком последовательности как функции, заданной на множестве натуральных чисел, являются отдельные, изолированные точки координатной плоскостиyn=3n-2 задание Последовательности заданы формуламиan=n4an=n+4an=2n-5an=(-1)nn2an= -n-2an=3n-11. Впишите пропущенные члены последовательности1;___;81;___;625;…5;___;___;___;9-1;4;___;___; -25;…-3; -4;___;___; -7…2; По преданию, индийский царь Шерам, восхищенный  остроумием шахматной Среднеазиатский математик Бернулли получил верный ответ:       18 446 744 073 709 551 ПРОТОРГОВАЛСЯ ЛИ КУПЕЦ ? Некто продавал коня и просил за него 1000 РЕШЕНИЕ:всего гвоздей 24 штуки, за все гвозди купец должен заплатить 1 + Свойства числовых последовательностей Числовая последовательность называется возрастающей, если каждый ее член ПримерПоследовательность кубов натуральных чисел1,8,27 УБЫВАЮЩАЯ Числовая последовательность называется убывающей, если каждый ее член (кроме первого) Пример Монотонность Вместе возрастающие и убывающие последовательности называются монотонными последовательностями. Определить монотонность1)-1,-4,-9,-16….2)-1,0,1,2….3)-1,1,-1,1 Ограниченность сверху Определение. Последовательность  a1,  a2,  a3,  … называется ограниченной сверху, Пример1,-1,-3,-5Ограничена сверху М =1 Ограниченность снизуОпределение. Последовательность  a1,  a2,  a3,  … называется ограниченной снизу, если для ПримерОграничена и сверху и снизуМ=1M=0 Упражнение 1Укажите номер функции, являющейся числовой последовательностью Найдите первые пять членов последовательности заданной рекуррентноY1=2Yn=yn-1+5Упражнение 2 Упражнение 3 Упражнение 4Укажите номер убывающей последовательности Упражнение 5Является ли ограниченной последовательность
Слайды презентации

Слайд 2 Продолжи ряд
1, 2, 3, 4, 5, 6
12,

Продолжи ряд1, 2, 3, 4, 5, 6 12, 10, 8, 6,

10, 8, 6, 4
6, 9, 12, 15, 18,

21
2, 4, 8, 16, 32
1, 4, 16

Слайд 3 Последовательности составляют такие элементы природы, которые можно пронумеровать

Последовательности составляют такие элементы природы, которые можно пронумеровать Дни неделиКлассыВшколеДома наулице Квартиры вдоме Номерасчетов вбанкеНазвание месяцев


Дни
недели
Классы
В
школе

Дома
на
улице
Квартиры
в
доме
Номера
счетов
в
банке
Название
месяцев

Слайд 4 Найдите закономерности и покажите их стрелками
В порядке

Найдите закономерности и покажите их стрелками В порядке возрастания положительные нечетные

возрастания
положительные
нечетные числа
В порядке убывания
Правильные дроби
с

числителем,
равным 1

В порядке возрастания
положительные числа,
кратные7

В порядке убывания
положительные
двузначные числа

7;14;21;28…

99;98;97…

1;3;5;7;9…



Слайд 5 Определение
Функцию y=f(x), определенную на множестве натуральных

Определение Функцию y=f(x), определенную на множестве натуральных чисел xϵN (или его

чисел xϵN (или его конечном подмножестве), называют числовой последовательностью

и обозначают
y=f(n), или
y1,y2,…,yn,…. или (yn).

Слайд 6
Числа y1, y2, …,

Числа y1, y2, …, yn называют членами последовательности, а

yn называют членами последовательности, а член с номером n

– ее
n-членом, его еще называют общим членом.

Слайд 7 Члены последовательности обозначаются так:
a1
a2
a3
a4
…
an
Первый
член
Второй
член
Третий
член
Четвертый
член
n-член
последовательности

Члены последовательности обозначаются так: a1a2a3a4…anПервыйчленВторойчленТретийчленЧетвертыйчленn-членпоследовательности

Слайд 8 Задать числовую последовательность
— это значит указать, как отыскивается

Задать числовую последовательность— это значит указать, как отыскивается тот или иной

тот или иной ее член, если известен номер занимаемого

им   места.

Слайд 9 Способы описания последовательности
Последовательности можно задавать различными

Способы описания последовательности Последовательности можно задавать различными способами, среди которых особенно важны три: аналитическийсловесный рекуррентный

способами, среди которых особенно важны три:
аналитический
словесный
рекуррентный

Слайд 10 Формула
1. Последовательность задана аналитически, если задана формула ее

Формула1. Последовательность задана аналитически, если задана формула ее n-го члена: yn

n-го члена: yn = f(n).
Пример: yn = 2n –

1
Y1=2*1-1=1
Y2=2*2-1=2
Y3=2*3-1=5
Y4=2*4-1=7
Y5=2*5-1=9
последовательность нечетных чисел: 1, 3, 5, 7, 9, …

Слайд 11 Описательный способ задания числовой последовательности состоит в том,

Описательный способ задания числовой последовательности состоит в том, что объясняется, из

что объясняется, из каких элементов строится последовательность.
Пример 1.


«Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2.
«Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, ….

Слайд 12 Рекурентный
Рекуррентный способ задания последовательности состоит в том, что

РекурентныйРекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее

указывается правило, позволяющее вычислить n-й член последовательности, если известны

ее предыдущие члены.

Слайд 13 Пример рекуррентного задания
Пример 1.
y1 = 3;
yn

Пример рекуррентного заданияПример 1. y1 = 3; yn = yn–1 +

= yn–1 + 4, если n = 2, 3,

4,….
Здесь
y1 = 3;
y2 = 3 + 4 = 7;
y3 = 7 + 4 = 11; ….

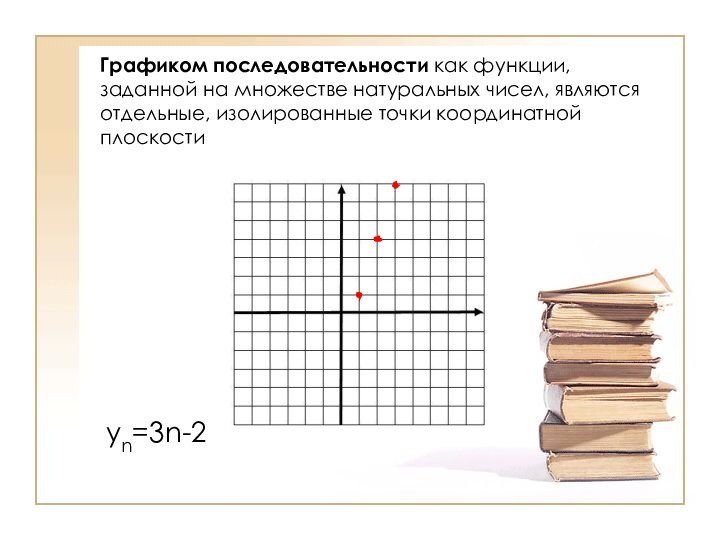
Слайд 14 Графиком последовательности как функции, заданной на множестве натуральных

Графиком последовательности как функции, заданной на множестве натуральных чисел, являются отдельные, изолированные точки координатной плоскостиyn=3n-2

чисел, являются отдельные, изолированные точки координатной плоскости
yn=3n-2




Слайд 15 задание
Последовательности заданы формулами


an=n4
an=n+4
an=2n-5
an=(-1)nn2
an= -n-2
an=3n-1
1. Впишите пропущенные члены

задание Последовательности заданы формуламиan=n4an=n+4an=2n-5an=(-1)nn2an= -n-2an=3n-11. Впишите пропущенные члены последовательности1;___;81;___;625;…5;___;___;___;9-1;4;___;___; -25;…-3; -4;___;___;

последовательности
1;___;81;___;625;…
5;___;___;___;9
-1;4;___;___; -25;…
-3; -4;___;___; -7…
2; 8;___;___;___...
___;-4;___;___;-7
2. Укажите, какими числами являются

члены этих последовательностей


Положительные
и отрицательные

положительные

отрицательные

16

256

-9

16

-5

-6

6

7

8

-3

-5

-6

26

80

242


Слайд 16

Слайд 17 По преданию, индийский царь

По преданию, индийский царь Шерам, восхищенный  остроумием шахматной игры,

Шерам, восхищенный  остроумием шахматной игры, призвал к себе изобретателя

шахмат Сету и сказал ему: «Я желаю достойно вознаградить тебя ! Исполню любое твое желание…» Сета попросил положить на первую клетку доски 1 пшеничное зерно, на вторую – 2  зерна, на третью – 4 зерна и т. д.  Сколько нужно зерен ?   

Слайд 18 Среднеазиатский математик Бернулли получил верный ответ:       18 446 744

Среднеазиатский математик Бернулли получил верный ответ:       18 446 744 073 709

073 709 551 615 зерен.
Такое количество зерен пшеницы можно

собрать лишь с урожая планеты, поверхность которой в 2000 раз больше поверхности Земли.

Слайд 19 ПРОТОРГОВАЛСЯ ЛИ КУПЕЦ ?
Некто продавал коня и

ПРОТОРГОВАЛСЯ ЛИ КУПЕЦ ? Некто продавал коня и просил за него

просил за него 1000 рублей. Купец ска­зал, что цена

велика, "Хорошо,-ответил продавец, если ты гово­ришь, что конь дорого стоит, то возьми его себе даром, а заплати только за одни гвозди на его подковах, а гвоздей на его каждой подкове по 6 штук, и будешь ты мне за них платить таким образом: за первый гвоздь полушку, за второй - две полушки, за третий 4 полушки, и так далее за все гвозди: за каждый в два раза больше чем предыдущий". Купец согласился, проторговался ли купец?

Слайд 20 РЕШЕНИЕ:
всего гвоздей 24 штуки,
за все гвозди купец

РЕШЕНИЕ:всего гвоздей 24 штуки, за все гвозди купец должен заплатить 1

должен заплатить
1 + 2 + 2*2 + 2*2*2+

+...+2*2*...*2 полушек
23 раза и того получаем 41943 рубля и 15 полушек.

Слайд 21 Свойства числовых последовательностей
Числовая последовательность называется возрастающей,

Свойства числовых последовательностей Числовая последовательность называется возрастающей, если каждый ее член

если каждый ее член больше предыдущего, иными словами, если

для всякого  n > 1  верно неравенство  an > a n – 1.

Слайд 22 Пример
Последовательность кубов натуральных чисел
1,8,27

ПримерПоследовательность кубов натуральных чисел1,8,27

Слайд 23 УБЫВАЮЩАЯ
Числовая последовательность называется убывающей, если каждый

УБЫВАЮЩАЯ Числовая последовательность называется убывающей, если каждый ее член (кроме первого)

ее член (кроме первого) меньше предыдущего, иными словами, если

для всякого  n > 1  верно неравенство  an < a n – 1.

Слайд 24 Пример

Пример

Слайд 25 Монотонность
Вместе возрастающие и убывающие последовательности называются

Монотонность Вместе возрастающие и убывающие последовательности называются монотонными последовательностями.

монотонными последовательностями.

Слайд 26 Определить монотонность
1)-1,-4,-9,-16….
2)-1,0,1,2….
3)-1,1,-1,1

Определить монотонность1)-1,-4,-9,-16….2)-1,0,1,2….3)-1,1,-1,1

Слайд 27 Ограниченность сверху
Определение. Последовательность  a1,  a2,  a3, 

Ограниченность сверху Определение. Последовательность  a1,  a2,  a3,  … называется ограниченной сверху,

… называется ограниченной сверху, если для ее такое число 

M,  что неравенство   an

Слайд 28 Пример
1,-1,-3,-5
Ограничена сверху М =1

Пример1,-1,-3,-5Ограничена сверху М =1

Слайд 29 Ограниченность снизу
Определение. Последовательность  a1,  a2,  a3,  … называется

Ограниченность снизуОпределение. Последовательность  a1,  a2,  a3,  … называется ограниченной снизу, если

ограниченной снизу, если для ее такое число  m,  что

неравенство   an >m  выполняется для всех номеров  n.

Слайд 30 Пример
Ограничена и сверху и снизу
М=1
M=0

ПримерОграничена и сверху и снизуМ=1M=0

Слайд 31 Упражнение 1
Укажите номер функции, являющейся числовой последовательностью

Упражнение 1Укажите номер функции, являющейся числовой последовательностью

Слайд 32 Найдите первые пять членов последовательности заданной рекуррентно
Y1=2
Yn=yn-1+5
Упражнение 2

Найдите первые пять членов последовательности заданной рекуррентноY1=2Yn=yn-1+5Упражнение 2

Слайд 33 Упражнение 3

Упражнение 3

Слайд 34 Упражнение 4
Укажите номер убывающей последовательности

Упражнение 4Укажите номер убывающей последовательности
  • Имя файла: posledovatelnosti.pptx
  • Количество просмотров: 170
  • Количество скачиваний: 0
- Предыдущая Воспитание экологической культуры посредством краеведческого подхода
Следующая - Полезные ископаемые Кемеровской области

Похожие презентации

Презентация к уроку алгебры в 11 классе на тему Свойства логарифма Презентация к уроку алгебры в 11 классе на тему Свойства логарифма 187
Решение задач с помощью десятичных дробей Решение задач с помощью десятичных дробей 157
Обратная пропорциональность Обратная пропорциональность 171
Саморазвитие интеллекта школьника на уроках математики Саморазвитие интеллекта школьника на уроках математики 171
Примеры комбинаторных задач (9 класс) Примеры комбинаторных задач (9 класс) 235
Презентация к семинару , мастер класс по математике Решение задач. Презентация к семинару , мастер класс по математике Решение задач. 209
Презентация по математике Подготовка к ОГЭ урок-игра Математик-бизнесмен Презентация по математике Подготовка к ОГЭ урок-игра Математик-бизнесмен 155
Решение систем уравнений графическим способом Решение систем уравнений графическим способом 161
Занимательная математика 8-9 класс Занимательная математика 8-9 класс 236
Презентация по алгебре на тему Уравнения с модулем Презентация по алгебре на тему Уравнения с модулем 167
Игры по алгебре в 8 классе Математическая эстафе Игры по алгебре в 8 классе Математическая эстафе 149
Наглядное представление статистической информации Наглядное представление статистической информации 147
Сложение и вычитание дробей с одинаковыми знаменателями Сложение и вычитание дробей с одинаковыми знаменателями 136
Свойства степени с натуральным показателем Свойства степени с натуральным показателем 141
Франсуа Виет и его теорема Франсуа Виет и его теорема 148
Математическая теория вероятности Математическая теория вероятности 239
Презентация по геометрии к зачёту по теме Перпендикулярность прямой и плоскости Презентация по геометрии к зачёту по теме Перпендикулярность прямой и плоскости 158
Исследование графика линейной функции Исследование графика линейной функции 173
Исследовательский проект Решение квадратных уравнений Исследовательский проект Решение квадратных уравнений 399
В мире животных. Занимательная математика В мире животных. Занимательная математика 153
Применение свойств функций к решению уравнений и неравенств Применение свойств функций к решению уравнений и неравенств 157
Презентация Ключевые задачи для подготовки к экзаменам по теории вероятностей, 11 класс Презентация Ключевые задачи для подготовки к экзаменам по теории вероятностей, 11 класс 181
Презентация по математике на тему: логарифмическая функция Презентация по математике на тему: логарифмическая функция 182
Теорема Виета Теорема Виета 169
Рациональные уравнения. Алгебра, 11 класс. Подготовка к решению С1 Рациональные уравнения. Алгебра, 11 класс. Подготовка к решению С1 174
Понятие логарифма Понятие логарифма 156
Задачи по теории вероятности Задачи по теории вероятности 193
Интеграл. Площадь криволинейной трапеции Интеграл. Площадь криволинейной трапеции 178
Элементы комбинаторики, статистики и теории вероятностей. Задания из Открытого банка заданий ЕГЭ, профильный уровень, страница 10 Элементы комбинаторики, статистики и теории вероятностей. Задания из Открытого банка заданий ЕГЭ, профильный уровень, страница 10 185
Такое далёкое и близкое прошлое Такое далёкое и близкое прошлое 177