и построением их графического изображения,
представить систематизацию функций не
по видам, а по методам построения их графиков.Цель элективного курса
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


























Цель элективного курса
Задачи элективного курса
Содержание
х
у
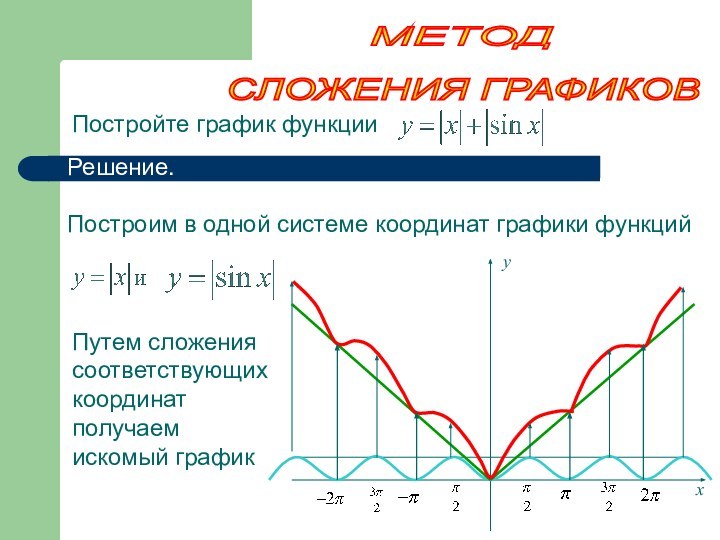
МЕТОД
1
у
1
-1
-1
-7
-5
5
7
х
Множества точек на плоскости.
Заметим, что график симметричен относительно осей координат.
Для I четверти система примет вид:
Общие признаки задач подходящих
под рассматриваемый метод
В задаче дан один
параметр а и одна
переменная х
Они образуют некоторые
аналитические выражения
F (x;a), G (x;a)
Графики уравнений
F(x;a)=0,G(x;a)=0
строятся несложно
1.Строим графический образ
2.Пересекаем полученный график прямыми
перпендикулярными параметрической оси
3.«Считываем» нужную информацию
Схема
решения:
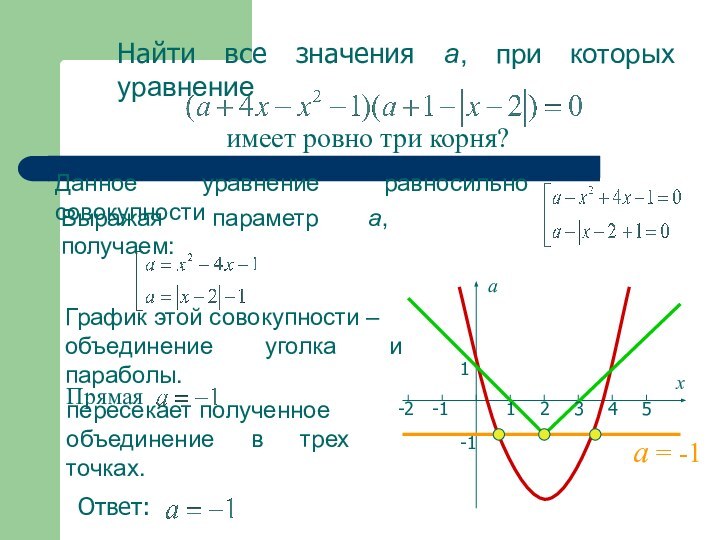
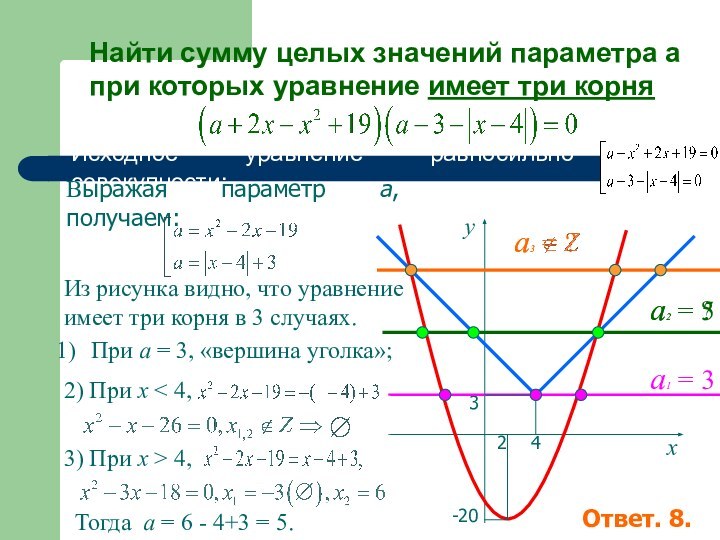
пересекает полученное
объединение в трех точках.
имеет ровно три корня?
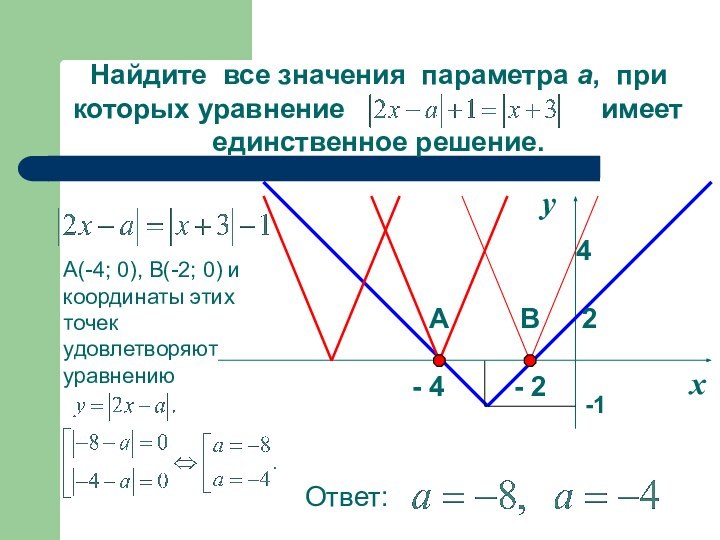
Ответ:
1
2
3
4
5
-1
-2
-1
1
х
а
а = -1
Прямая
График этой совокупности –объединение уголка и параболы.
2
А
В
А(-4; 0), В(-2; 0) и координаты этих точек удовлетворяют уравнению
-1
1.ОДЗ
2. Корни
3. Ось
4. Знаки на
интервалах
5. Ответ.
Метод интервалов:
Метод областей:
ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ
- 1
- 1
1
1
х
у
0
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
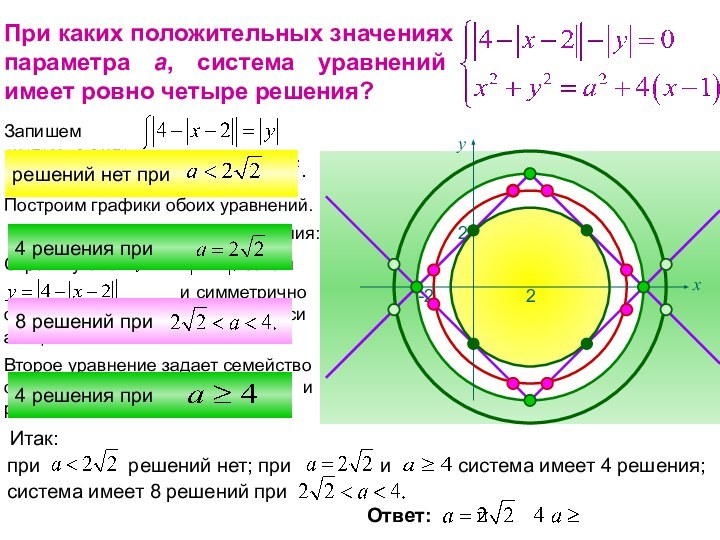
4 решения при а = 1
Ответ:
решений нет, если
8 решений, если
4 решения, если
.
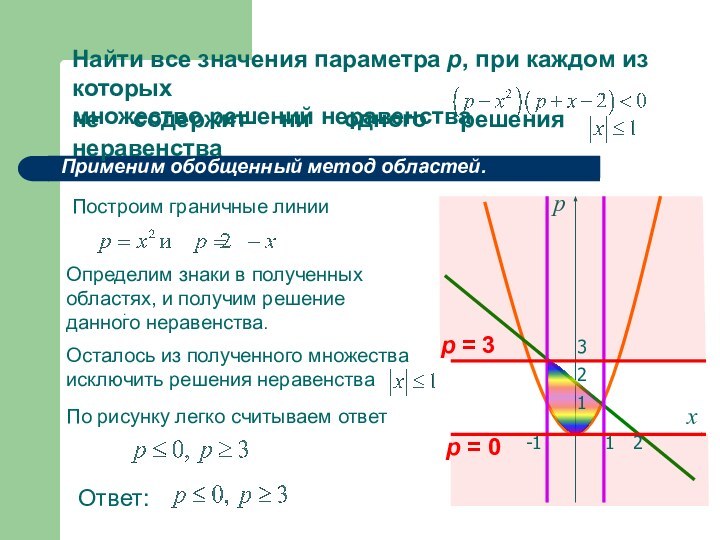
Применим обобщенный метод областей.
Определим знаки в полученных областях, и получим решение данного неравенства.
По рисунку легко считываем ответ
Ответ:
Построим граничные линии
р = 3
р = 0
-1
1
2
3
1
2
Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.
Построим графический образ соответствий, входящих в систему.
3
3
4
4
Очевидно, что условие задачи выполняется при
Ответ: