- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике по теме Квадратные уравнения (8 класс)
Содержание
- 2. «Никогда не считай, что ты знаешь все, что тебе уже больше нечему учиться» Н.Д.Зелинский
- 3. Сформулируйте определение квадратного уравнения.2. Объясните, в
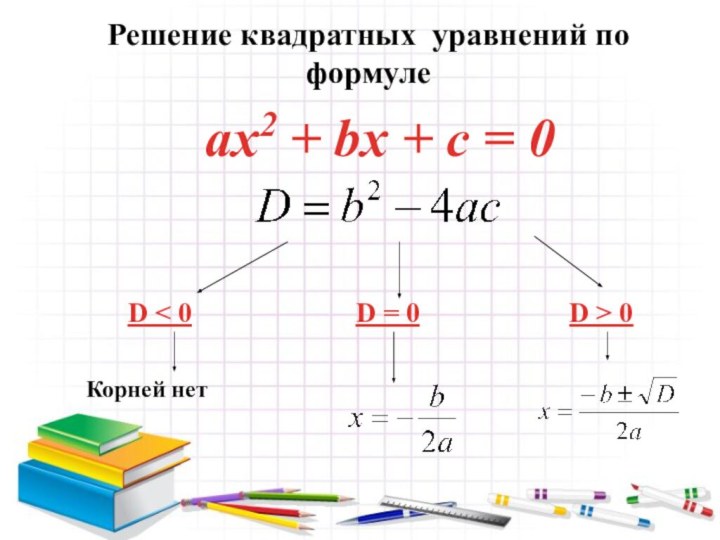
- 4. D < 0D = 0D >
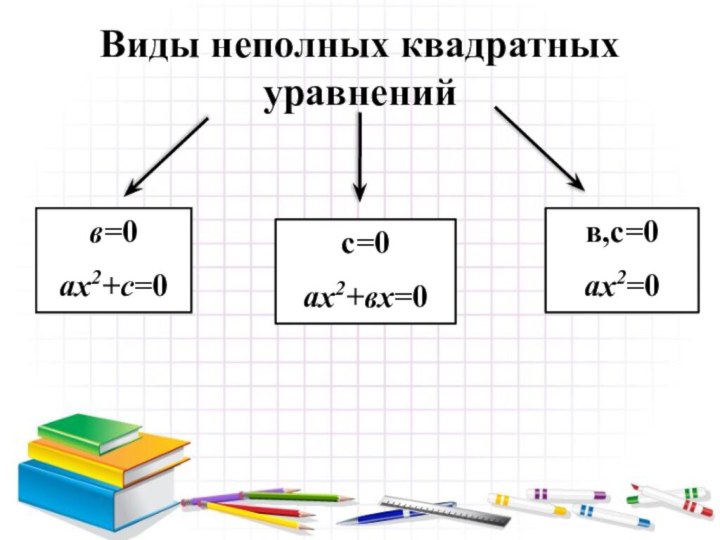
- 5. Виды неполных квадратных уравненийв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0
- 6. b = 2k (чётное число)Решение квадратных уравнений
- 7. Устно решить уравнения:5;-40;32Нет решений1;7
- 8. Теорема ВиетаСумма корней приведённого квадратного уравнения равна
- 9. В 13 – 16 веках
- 10. 1. х2-88х=0 2. х2-26х+169=03. 4. х2-20х=6х-105 5. 2(7х-6)2+3(7х-6)-5=0 6. х2=2-х7.
- 11. Методы решений квадратных уравнений:по формуле корней;по формуле
- 12. Устно решить уравнение:2015x2 -2016x+1=0
- 13. Квадратные уравнения
- 14. 0000 1; ;11;;1
- 15. 00001;1;1;1;
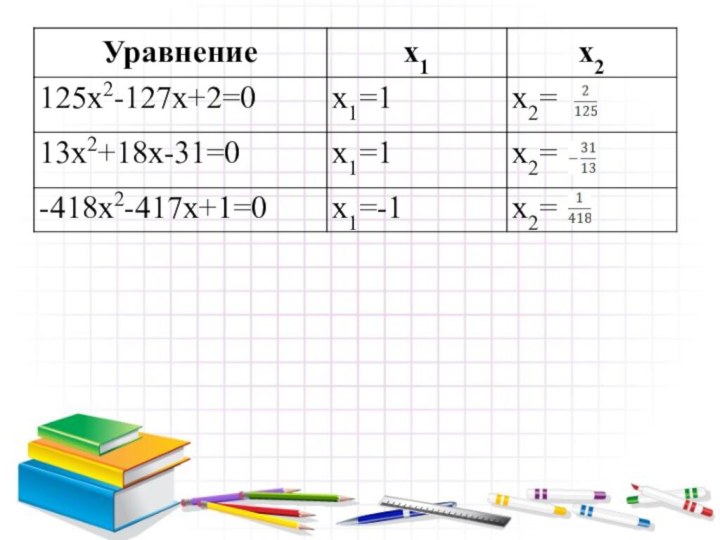
- 16. Если в уравнении ax2+bx+c=0 сумма коэффициентов a+b+c=0, то x1=1; x2=
- 17. 75-5357 -53-1;-1;-1;-1;
- 18. -18-14-75-145-7-18-1;-1;15-1;-4-1;
- 19. Если в уравнении ax2+bx+c=0 сумма коэффициентов a+с=b, то x1=-1; x2=-
- 22. Устно решить уравнение:2015x2 -2016x+1=0(x1=1;x2= )
- 23. Самостоятельная работа I группа(х2+3)2-7(х2+3)+12=0 II
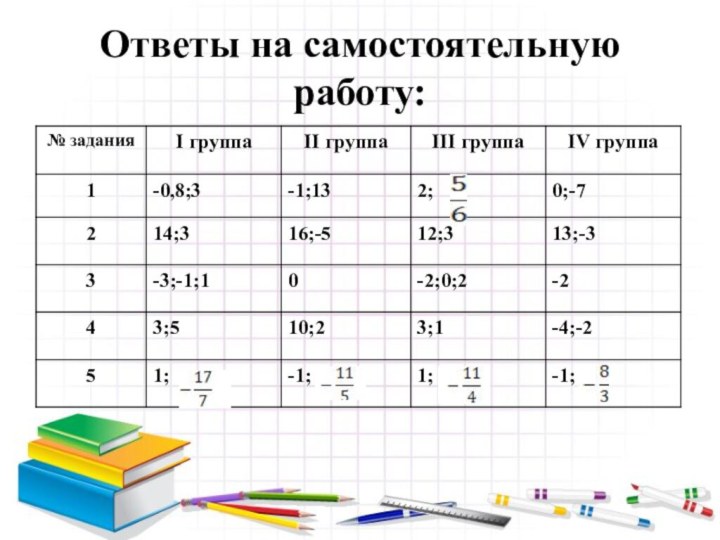
- 24. Ответы на самостоятельную работу:
- 25. Домашняя работаРешить уравнение разными методами: 11(3х-4)2+6(3х-4)-17=0
- 26. Скачать презентацию
- 27. Похожие презентации
«Никогда не считай, что ты знаешь все, что тебе уже больше нечему учиться» Н.Д.Зелинский





















Слайд 3
Сформулируйте определение квадратного уравнения.
2. Объясните, в чём
заключается смысл ограничения в определении квадратного уравнения (а ≠
0).3. Перечислите виды квадратных уравнений.
4. Какое квадратное уравнение называется неполным? Приведите пример.
5. Какое квадратное уравнение называется приведённым? Приведите пример.
6. Способы решения полного квадратного уравнения?
Вопросы
теоретической разминки:
Слайд 6
b = 2k (чётное число)
Решение квадратных уравнений по
формуле, когда b- четное число
ax2 + bx + c
= 0
Слайд 8
Теорема Виета
Сумма корней приведённого квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение корней равно
свободному члену.x1 + x2 = -p
x1 · x2 = q
Слайд 9 В 13 – 16 веках даются
отдельные методы решения различных видов квадратных уравнений. Слияние этих
методов произвел в 1544 году немецкий математик – Михаэль Штифель. Это было настоящее событие в математике.
Слайд 10
1. х2-88х=0
2. х2-26х+169=0
3.
4. х2-20х=6х-105
5. 2(7х-6)2+3(7х-6)-5=0
6. х2=2-х
7. 5х2+8х-4=0
1.по
формуле корней
2.по теореме Виета
3.по формуле с четным вторым коэффициентом
4.разложение
левой части на множители5.метод выделения квадрата двучлена
6.введение новой переменной
7.графически
Слайд 11
Методы решений квадратных уравнений:
по формуле корней;
по формуле с
четным вторым коэффициентом;
по теореме Виета;
разложение левой части на множители;
метод
выделения квадрата двучлена;введение новой переменной;
графически.
Слайд 23
Самостоятельная работа
I группа
(х2+3)2-7(х2+3)+12=0
II группа
3(6х2-х)2-4(6х2-х)+1=0
III группа
2(х2-1)2-13(х2-1)-24=0
IV группа
(х2-4х)2+9(х2-4х)+20=0
0;-1;1
-3;3
2