Слайд 2
Характеристика преобразований графиков функций у=mf(x), y=f(kx) из графика
функции y=f(x)
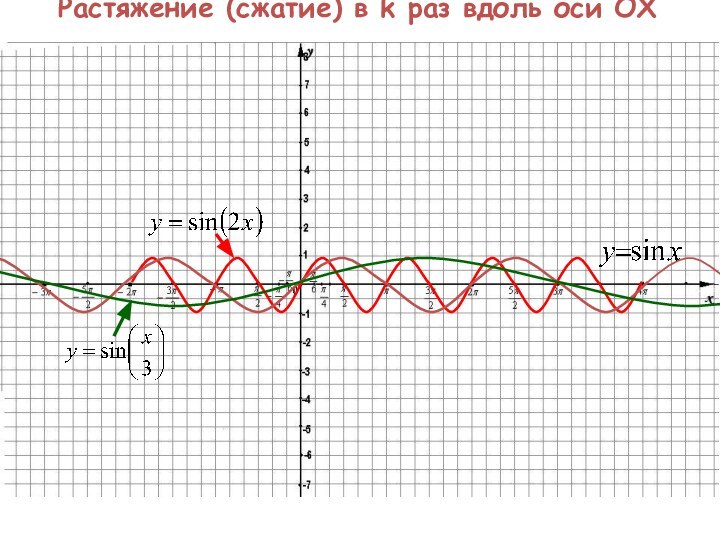
1. Если известен график функции y=f(x), то график
функции y=f(kx) строится посредством сжатия по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно:
-если k>1, то сжатие в k раз
-если 0
Слайд 3
Растяжение (сжатие)
в k раз вдоль оси OX
Слайд 4
2. Если известен график функции y=f(x), то график
функции y=kf(x)строится посредством растяжения вдоль оси Оy исходного графика,
пропорционально коэффициенту в k раз, а именно:
-если m>0, то растяжение в k раз
-если 0
Слайд 5
Растяжение (сжатие)
в k раз вдоль оси OY
Слайд 6
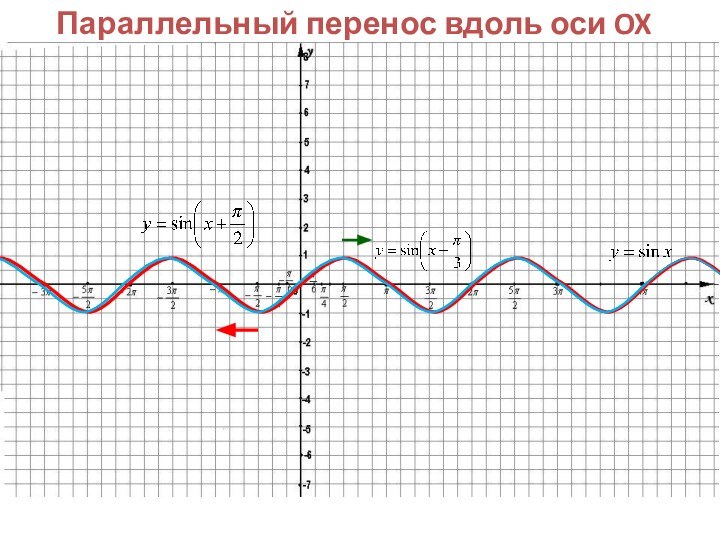
3. Если известен график функции y=f(x), то график
функции y=f(x+m) строится посредством сдвига по оси Оx исходного
графика(координатной оси) на m единиц, а именно:
-если m>0, то сдвиг на m единиц влево
-если m<0, то сдвиг на m единиц вправо
Слайд 7
Параллельный перенос
вдоль оси OX
Слайд 8
4. Если известен график функции y=f(x), то график
функции y=f(x)+m строится посредством сдвига по оси Оy исходного
графика(координатной оси) на m единиц, а именно:
-если m>0, то сдвиг на m единиц вверх
-если m<0, то сдвиг на m единиц вниз
Слайд 9
Параллельный перенос
вдоль оси OY
Слайд 10
5. График функции y=f(|x|) получается из графика =
y=f(x) следующим образом:
Часть графика лежащая над осью Ох сохраняется,
а его часть лежащая под осью Ох отображается симметрично относительно оси Оy
Слайд 12
6. График функции y=|f(x)| получается из графика =
y=f(x) следующим образом:
Часть графика лежащая над осью Ох сохраняется,
а его часть лежащая под осью Ох отображается симметрично относительно оси Ох
Слайд 14
7. Чтобы построить график функции y=|f(|x|)| надо: построить
график функции y=f(x) при x≥0. Отобразить полученную часть симметрично
относительно оси Оy. Участки полученного графика, лежащие ниже оси Ox зеркально отобразить относительно этой оси
Слайд 16
Характеристика графика гармонического колебания
(y=mf(kx+a)+b)
Построение графика этой функции
осуществляется в несколько этапов:
Осуществим параллельный перенос системы координат, поместив
начало новой системы х‘у’ в точку О’ (- ; 0)
2. В системе х‘у’ построим график функции у’=sin x (при этом можно ограничиваться одной полуволной)
3. Осуществим сжатие или растяжение последнего графика от оси у’ с коэффициентом А, получим требуемый график.
Слайд 17
Функция синус
Область определения функции — множество R всех
действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е.
синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R.
sin x = 0 при x = π·k, k ∈ Z.
sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z.
sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
Функция возрастает от −1 до 1 на промежутках:
Функция убывает от −1 до 1 на промежутках:
Наибольшее значение функции sin x = 1 в точках:
Наименьшее значение функции sin x = −1 в точках:
Слайд 18
Функция косинус
Область определения функции — множество R всех
действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е.
косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R.
cos x = 0 при
cos x > 0 для всех
cos x < 0 для всех
Функция возрастает от −1 до 1 на промежутках:
Функция убывает от −1 до 1 на промежутках:
Наибольшее значение функции sin x = 1 в точках:
Наименьшее значение функции sin x = −1 в точках:
Слайд 19
Функция тангенс
Область определения функции — множество всех действительных
чисел, кроме
Множество значений функции — вся числовая прямая, т.е.
тангенс — функция неограниченная.
Функция нечетная: tg(−x)=−tg x для всех х из области определения.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения.
tg x = 0 при
tg x > 0 для всех
tg x < 0 для всех
Функция возрастает на промежутках: