Презентация на тему по математике на тему Координаты точки и координаты вектора 11 класс

строить точку по заданным координатам и находить координаты точки,

прямой?
Одной.
2. Сколькими координатами может быть задана точка в

Двумя.

3. Сколькими координатами может быть задана точка в пространстве?

Вопрос урока.

Оz
Оz Оx

Оy Оx




x
z
1
1
1


A
A (1; 1;

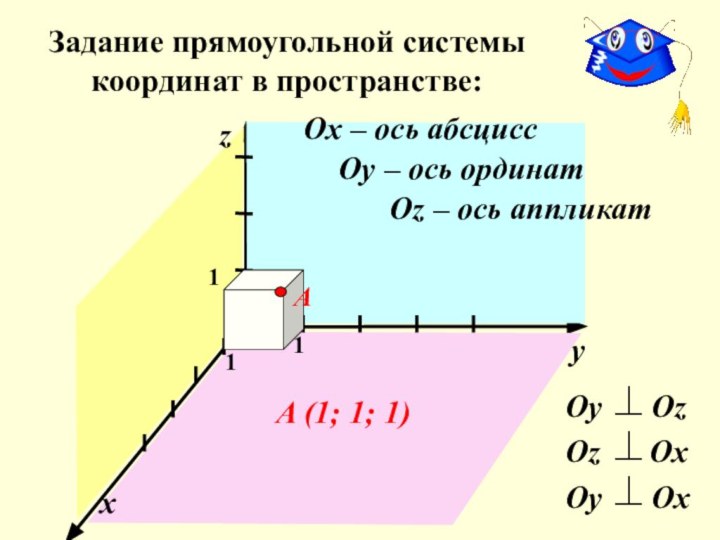
Ох – ось абсцисс

Оу – ось ординат

Оz – ось аппликат

три координатные плоскости: (Oxy), (Oyz) и(Oxz).

(х; 0; 0)
Оz (0; 0; z)
в координатной плоскости
Оху (х;

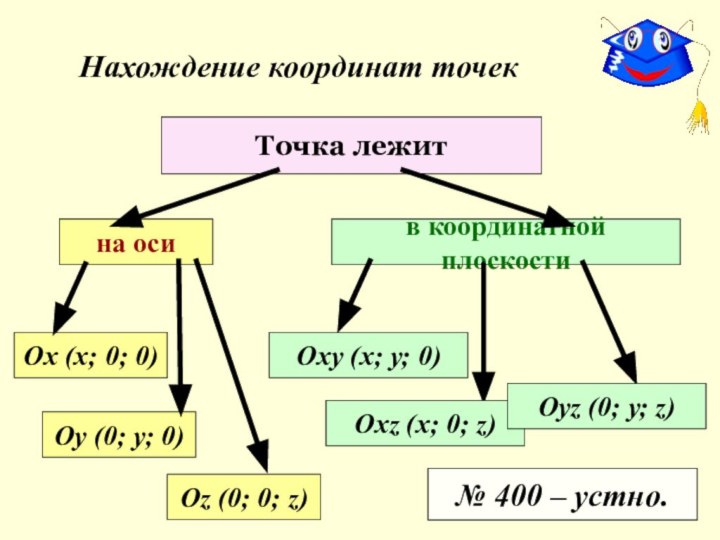
Охz (х; 0; z)

Оуz (0; у; z)

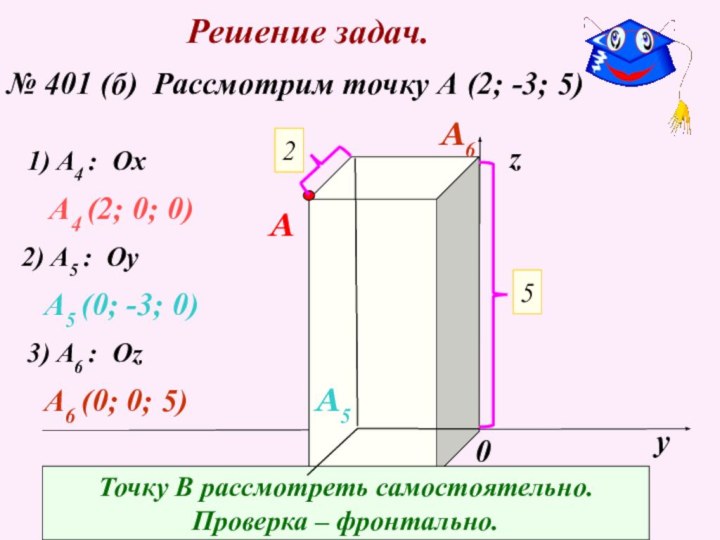
№ 400 – устно.

-3; 5)




х
у
z
0




2
5
-3
A
1) A1 : Oxy
A1
A1 (2; -3; 0)
A2
2) A2

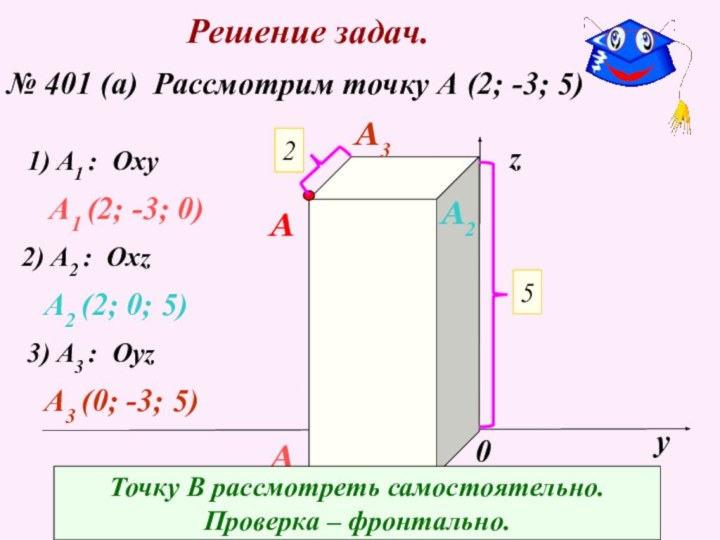
A2 (2; 0; 5)

3) A3 : Oyz

A3

A3 (0; -3; 5)

Точку В рассмотреть самостоятельно.
Проверка – фронтально.

-3; 5)




х
у
z
0




2
5
-3
A
1) A4 : Ox
A4
A4 (2; 0; 0)
A5
2) A5

A5 (0; -3; 0)

3) A6 : Oz

A6

A6 (0; 0; 5)

Точку В рассмотреть самостоятельно.
Проверка – фронтально.

- ?
D1 - ?
A (0;0;0)
B (0;0;1)
D (0;1;0)
В1 (1; 0;

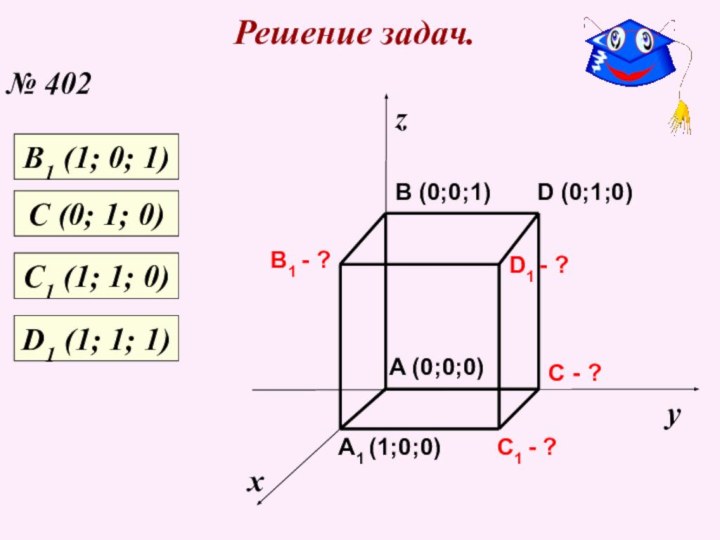
С (0; 1; 0)

С1 (1; 1; 0)

D1 (1; 1; 1)

0; 3)

С
D (4; 0; 4)



D

-1)

1
1
1


В
С (0; 5; 0)

С
D (-3; -1; 0)



D

начала координат единичный вектор, т.е. вектор, длина которого равна

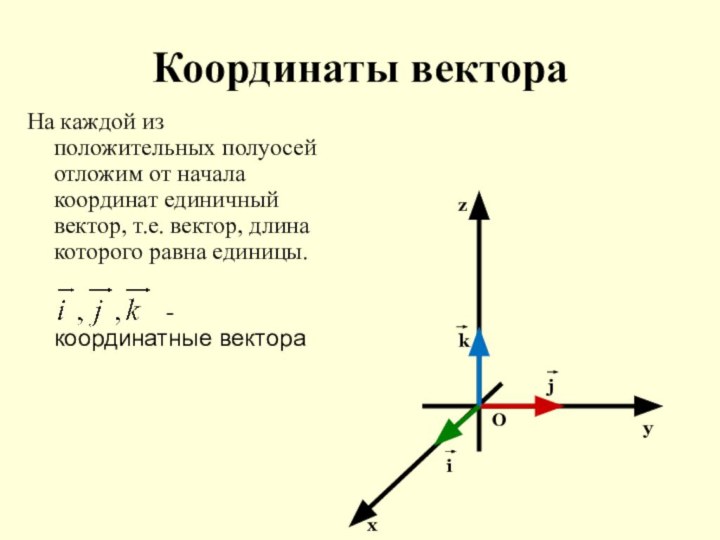
j

k

i

y

z

x

O

по координатным векторам, т.е. представить в виде

векторы имеют равные координаты.

Пусть



, тогда





Следовательно
х1 = х2; у1 =

координата суммы двух (и более) векторов равна сумме соответствующих

Дано:

Доказать:

Следовательно

координата произведения вектора на число равна произведению соответствующей координаты

Дано:

Доказать:

α – произв.число

4. Каждая координата разности двух векторов равна число равна разности соответствующих координат на этих векторов.

Дано:

Доказать:

Доказательства выполнить дома.