Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре на тему Квадратные уравнения

Содержание

Цели: 1.Систематизация знаний по теме «Квадратные уравнения»; 2.Развитие интереса к предмету. Задачи: 1.Знать определение квадратного уравнения, типы, методы решения; 2.Понимать отличительные особенности квадратных уравнений;
Квадратные уравнения Учитель математикиГБОУ Лицей №126 г.Санкт-ПетербургОльшина Марина Валерьевна Цели: 1.Систематизация знаний по теме «Квадратные уравнения»; Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. 325 – 409 г.г. по Р. Х. знаменитый александрийский математик.ДИОФАНТВ арифметике Диофанта Задача ДиофантаНайти два числа, зная, что их сумма равна 20, а произведение Найти два числа, зная, что их сумма равна 20, а произведение — Интересные способы решения квадратных уравнений встречаются в трудах индийского ученого Бхаскары (600 Задача знаменитого индийского математика XII в. Бхаскары: Обезьянок резвых стая всласть Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных Квадрат и число 21 равны 10 корням. Найти корень (подразумевается корень уравнения Квадратным уравнением называется уравнение вида Определение корня Корнем квадратного уравнения называют такое значение переменной х, при котором Типы квадратных уравнений полныенеполныеа) б)в) a)9х2=0;б)3x+ x2+1=0;в)2x2-32=0;г) x2+4x=0;д)2х2+5х-7=0; е)12-х2+3х=0.Данные уравнения разбейте на полные и неполные: а) 9х2= 0; в) 2х2-32=0; г) х2+4х=0. 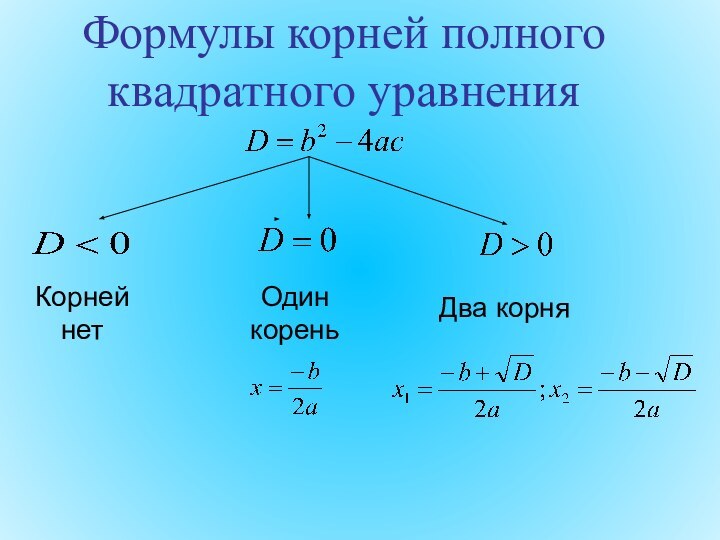Способы решения неполных квадратных уравненийc=0b=0b=0;c=0 Решите уравнения: Формулы корней полного квадратного уравненияКорней нетОдин кореньДва корня Формула четного коэффициентаb=2ka=1 Теорема Виета- корни квадратного уравнения 1.Найдите корни квадратного уравнения, не используя формулы корней:Корней нет2.Составьте приведенное квадратное уравнение, Применение квадратных уравнений-решение рациональных уравнений;-решение иррациональных уравнений; -решение задач; -разложение квадратного 1.Решите уравнения:2.Сократите дробь:3.При каком значении параметра a уравнение Проверь себя!Ответ: 1;2. Проверь себя! Корней нетОтвет: -4;4. Проверь себя!Проверка:Ответ: 1.-2-посторонний корень Проверь себя!2.Сократить дробь: Проверь себя!Квадратное уравнение имеет один корень, если D=0; Ответ: а=-6;а=6.3. Составьте математическую модель для решения задачи: В прямоугольном треугольнике один катет меньше Домашнее задание:1.Решите уравнения:2.Сократите дробь:3.При каком значении параметра а уравнение Использованные ресурсы1.Ш.А.Алимов.Алгебра.Учебник для 8 класса. М. :Просвещение, 20072.М.В.Ткачева.Алгебра 8 класс. Дидактические материалы
Слайды презентации

Слайд 2 Цели:
1.Систематизация знаний по теме

Цели: 1.Систематизация знаний по теме «Квадратные уравнения»; 2.Развитие

«Квадратные уравнения»; 2.Развитие интереса к предмету.
Задачи:
1.Знать

определение квадратного уравнения, типы, методы решения; 2.Понимать отличительные особенности квадратных уравнений; 3.Применять полученные знания при решении рациональных, иррациональных уравнений, сокращении дробей, решении задач.

Слайд 3 Квадратные уравнения умели решать около 2000 лет до

Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

н. э. вавилоняне.

Слайд 4 325 – 409 г.г. по Р. Х. знаменитый

325 – 409 г.г. по Р. Х. знаменитый александрийский математик.ДИОФАНТВ арифметике

александрийский математик.
ДИОФАНТ
В арифметике Диофанта отсутствуют понятие отрицательного числа и

общие методы решения квадратных уравнений.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Слайд 5 Задача Диофанта
Найти два числа, зная, что их сумма

Задача ДиофантаНайти два числа, зная, что их сумма равна 20, а

равна 20, а произведение — 96.


Если бы искомые числа

были равны:

То произведение чисел было бы равно 100

ПРОТИВОРЕЧИЕ
С
УСЛОВИЕМ!!!

Слайд 6 Найти два числа, зная, что их сумма равна

Найти два числа, зная, что их сумма равна 20, а произведение

20, а произведение — 96.



Значит, одно из этих чисел

будет больше половины их суммы, т. е. (10 + х),
другое же меньше, т. е. (10 – х).
Разность между ними 2х.
Отсюда уравнение:
(10+x)(10—x) =96,
100 —x2 = 96.
x2 - 4 = 0
х = 2
Одно из искомых чисел равно 12, другое 8.
Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Слайд 7 Интересные способы решения квадратных уравнений встречаются в трудах

Интересные способы решения квадратных уравнений встречаются в трудах индийского ученого Бхаскары

индийского ученого Бхаскары
(600 – около 680г.г.).
И арабского ученого


Ал – Хорезми
(780 – около 850г.г.)

Слайд 8 Задача знаменитого индийского математика XII в. Бхаскары:

Задача знаменитого индийского математика XII в. Бхаскары: Обезьянок резвых стая всласть

Обезьянок резвых стая всласть поевши, развлекалась, их в квадрате

часть восьмая на поляне забавлялась, а двенадцать по лианам стали прыгать, повисая. Сколько ж было обезьянок, ты скажи мне, в этой стае?




Слайд 9 Решение Бхаскары свидетельствует о том, что он знал

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней

о двузначности корней квадратных уравнений.
Бхаскара пишет:


x2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 1024, получая затем:
x2 - 64х + 1024 = -768 + 1024,
(х - 32)2 = 256,
х - 32= ±16,
x1 = 16,       x2 = 48.


Слайд 10 Квадрат и число 21 равны 10 корням. Найти

Квадрат и число 21 равны 10 корням. Найти корень (подразумевается корень

корень (подразумевается корень уравнения х2 + 21 = 10х).

Решение

автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Задача Ал – Хорезми:


Слайд 11 Квадратным уравнением называется уравнение вида

Квадратным уравнением называется уравнение вида


где коэффициенты a,b,c-любые действительные числа, причем

Определение квадратного уравнения

Слайд 12 Определение корня
Корнем квадратного уравнения

называют такое значение

Определение корня Корнем квадратного уравнения называют такое значение переменной х, при

переменной х, при котором квадратный трехчлен

обращается в нуль;

Слайд 13 Типы квадратных уравнений
полные

неполные
а)

б)

в)

Типы квадратных уравнений полныенеполныеа) б)в)

Слайд 14 a)9х2=0;
б)3x+ x2+1=0;
в)2x2-32=0;
г) x2+4x=0;
д)2х2+5х-7=0;
е)12-х2+3х=0.

Данные уравнения разбейте на полные

a)9х2=0;б)3x+ x2+1=0;в)2x2-32=0;г) x2+4x=0;д)2х2+5х-7=0; е)12-х2+3х=0.Данные уравнения разбейте на полные и неполные:

и неполные:

Слайд 15 а) 9х2= 0;
в) 2х2-32=0;

а) 9х2= 0; в) 2х2-32=0; г) х2+4х=0. б) 3х+х2+1=0; д)2х2+5х-7=0; е)12-х2+3х=0. неполные: полные:

г) х2+4х=0.



б) 3х+х2+1=0;
д)2х2+5х-7=0;

е)12-х2+3х=0.


неполные:

полные:

Слайд 16 Способы решения неполных квадратных уравнений




c=0
b=0

b=0;c=0

Способы решения неполных квадратных уравненийc=0b=0b=0;c=0

Слайд 17 Решите уравнения:


Решите уравнения:

Слайд 18 Формулы корней полного квадратного уравнения



Корней нет

Один корень


Два корня

Формулы корней полного квадратного уравненияКорней нетОдин кореньДва корня

Слайд 19 Формула четного коэффициента
b=2k

a=1

Формула четного коэффициентаb=2ka=1

Слайд 20 Теорема Виета
- корни квадратного уравнения

Теорема Виета- корни квадратного уравнения

Слайд 21 1.Найдите корни квадратного уравнения, не используя формулы корней:



Корней

1.Найдите корни квадратного уравнения, не используя формулы корней:Корней нет2.Составьте приведенное квадратное

нет
2.Составьте приведенное квадратное уравнение, корнями которого являются числа 3

и -7:

Слайд 22 Применение квадратных уравнений
-решение рациональных уравнений;
-решение иррациональных уравнений;

Применение квадратных уравнений-решение рациональных уравнений;-решение иррациональных уравнений; -решение задач; -разложение квадратного трехчлена на множители; -сокращение дробей.

-решение задач;
-разложение квадратного трехчлена на множители;
-сокращение

дробей.

Слайд 23 1.Решите уравнения:
2.Сократите дробь:
3.При каком значении параметра a уравнение

1.Решите уравнения:2.Сократите дробь:3.При каком значении параметра a уравнение имеет один корень? Задание:

имеет один корень?

Задание:

Слайд 24 Проверь себя!
Ответ: 1;2.

Проверь себя!Ответ: 1;2.

Слайд 25 Проверь себя!

Корней нет

Ответ: -4;4.

Проверь себя! Корней нетОтвет: -4;4.

Слайд 26 Проверь себя!
Проверка:

Ответ: 1.
-2-посторонний корень

Проверь себя!Проверка:Ответ: 1.-2-посторонний корень

Слайд 27 Проверь себя!
2.Сократить дробь:

Проверь себя!2.Сократить дробь:

Слайд 28 Проверь себя!
Квадратное уравнение имеет один корень, если D=0;
Ответ:

Проверь себя!Квадратное уравнение имеет один корень, если D=0; Ответ: а=-6;а=6.3.

а=-6;а=6.
3.

Слайд 29 Составьте математическую модель для решения задачи:
В прямоугольном

Составьте математическую модель для решения задачи: В прямоугольном треугольнике один катет

треугольнике один катет меньше гипотенузы на 4 см, а

другой – на 8 см. Найдите гипотенузу.

Слайд 30 Домашнее задание:
1.Решите уравнения:
2.Сократите дробь:

3.При каком значении параметра а

Домашнее задание:1.Решите уравнения:2.Сократите дробь:3.При каком значении параметра а уравнение

уравнение

имеет один корень?
  • Имя файла: prezentatsiya-po-algebre-na-temu-kvadratnye-uravneniya.pptx
  • Количество просмотров: 167
  • Количество скачиваний: 0
- Предыдущая Презентация по русскому языку на тему: Сочинение по картине Рылова В голубом просторе (3 класс)
Следующая - Презентация по французскому язык на тему:Paris-Moscou-Maikop.

Похожие презентации

Построение графика квадратичной функции Построение графика квадратичной функции 157
Понятие корня n – й степени из действительного числа. Понятие корня n – й степени из действительного числа. 206
Применение производной к исследованию функции Применение производной к исследованию функции 124
Решение линейных и квадратных уравнений с параметрами в курсе математики основной школы Решение линейных и квадратных уравнений с параметрами в курсе математики основной школы 159
Презентация по математике на тему: Вспомни Всё Презентация по математике на тему: Вспомни Всё 142
Презентация по алгебре График квадратичной функции Презентация по алгебре График квадратичной функции 160
Линейная функция Линейная функция 120
Презентация Комплексные числа и действия с ними Презентация Комплексные числа и действия с ними 191
Алгебраические дроби (8 класс) Алгебраические дроби (8 класс) 206
Примеры логарифмических уравнений и неравенств Примеры логарифмических уравнений и неравенств 170
Арифметикалық квадрат түбірдің қасиеттері тақырыбындағы презентация Арифметикалық квадрат түбірдің қасиеттері тақырыбындағы презентация 225
Свойства арифметического корня П-ОЙ степени Свойства арифметического корня П-ОЙ степени 189
Презентация к мероприятию Математическая викторина Презентация к мероприятию Математическая викторина 168
Примеры комбинаторных задач Примеры комбинаторных задач 156
ЦОР по теории вероятностей ЦОР по теории вероятностей 251
Комбинаторика 9 класс Комбинаторика 9 класс 203
Презентация по алгебре на тему Арифметическая прогрессия Презентация по алгебре на тему Арифметическая прогрессия 168
Последовательности Последовательности 164
Решение неравенств второй степени Решение неравенств второй степени 139
Презентация по алгебре и началам анализа Логарифмы Презентация по алгебре и началам анализа Логарифмы 158
Презентация по алгебре Арифметическая прогрессия (9 класс) Презентация по алгебре Арифметическая прогрессия (9 класс) 198
Уравнения Уравнения 191
Многочлены Многочлены 173
Область определения функций Область определения функций 160
Системы счисления Системы счисления 177
Комбинаторные задачи и их решения Комбинаторные задачи и их решения 201
Метод рационализации Метод рационализации 207
Примеры применения производной Примеры применения производной 165
Пример игры по математике на тему Свойства степеней. Алгебра 7 класс Пример игры по математике на тему Свойства степеней. Алгебра 7 класс 199
Презентация по математике Множество действительных чисел Презентация по математике Множество действительных чисел 189