Слайд 2
Содержание
1 Понятие уравнения и его свойства
2 Методы решения уравнений
Метод разложения на множители
Метод введения новой переменной
Функционально-графический метод
Слайд 3
Теоретическая часть
1 Понятие уравнения (определение, равносильность)
2 Теоремы
о равносильности уравнений
3 Понятие алгебраического, рационального,
дробно- рационального, иррационального уравнений
4 Суть методов а) разложение на множители
б) замена переменной
в) функционально-графический
Слайд 4
Метод разложения на множители
Пример 1. Решить алгебраическое уравнение
:
(х-α)³+(х-b)³=(2х-α-b)³ .
Соберём все члены в левой части уравнения и сумму кубов (х-α)³+(х-b)³ разложим на множители. После этого в левой части можно выделить общий множитель 2х-α-b:
(2х-α-b)((х-α)²-(х-α)(х-b)+(х-b)²-(2х-α-b)²)=0,
(2х-α-b)(-3х²+3(α+b)х-3αb)=0.
Отсюда х₁ =(α+b):2, х₂=α, х₃=b.
Ответ:(α+b ):2; α; b.
Слайд 5
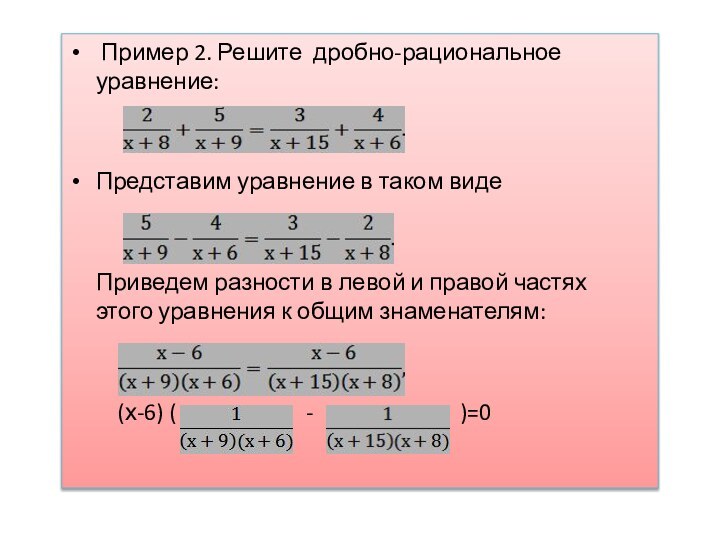
Пример 2. Решите дробно-рациональное уравнение:
Представим уравнение в
таком виде
Приведем разности в левой и
правой частях этого уравнения к общим знаменателям:
(х-6) ( - )=0
Слайд 6
Приравняем нулю каждый из
множителей в левой части последнего уравнения.
Получим х – 6 =0 или 8х= 66, учитывая при этом, что х=-9, х=-6,
х=-15, х= -8.
Тогда
Ответ: 6,-33/4.
Слайд 7
Пример 3.Решите уравнение:
Возведем обе части уравнения
в куб, пользуясь формулой
(a+b)³=a³+b³+3ab(a+b).
Будем
иметь:
Слайд 8
А теперь воспользуемся исходным уравнением, на основании
которого сумма в скобках равна 1:
Последнее уравнение также возведем
в куб:
(х-1)(2х-1)=(1-х)³, (х-1)(2х-1+(х-1)²)=0, (х-1)х²=0.
Отсюда х₁=1, х₂=х₃=0.
Проверка по первоначальному уравнению показывает, что значение х=1 ему удовлетворяет, а значение х=0 – не удовлетворяет.
Ответ: 1.
Слайд 9
Введение новой переменной
Пример 4. Решите уравнение:
(х-1)(х-2)(х-4)(х-8)= 4х2.
В левой части уравнения умножим первый
множитель на четвёртый, второй на третий, получим: (х²-9х+8)(х²-6х+8)=4х².
А дальше разделим обе части уравнения на х2, пользуясь тем, что значение х=0 не является корнем уравнения:
(x-9+ )(x-6+ )=4
Слайд 10
Введем подстановку: х-9+ =у. Будем иметь:
y(у+3)=4, у2+3у-4=0; у1=1, у2=-4.
В обоих случаях найдем
х, решая совокупность уравнений
х₁,₂=5
Ответ: 5 .
Слайд 11
Пример 5.Решите уравнение: (х+3)⁴+(х+5)⁴=16.
Положим х+4=y ,т. к.
=х+4.
Имеем: (y-1)⁴+(y+1)⁴=16.
Теперь нужно в левой части уравнения (y-1) и ( y+1) возвести в квадрат, а затем то, что получилось, ещё раз возвести в квадрат. После упрощений образуется биквадратное уравнение: y⁴+6y²-7=0.
Его корни y₁,₂ = . Отсюда х₁=-3, х₂=-5.
Ответ: -3; -5.
Слайд 12
Пример 6. Решите уравнение:
Отнимем от обеих частей
уравнения
для того, чтобы получить в левой
части квадрат разности:
А теперь очевидная подстановка = у.
Ответ: .
Слайд 13
Пример 7. Решите уравнение:
х2+8х+8=4(х+2)
Положим
=t.
При
это равенство равносильно равенству х+1=t2. Получаем систему рациональных уравнений:
Для ее решения выразим х через t из второго уравнения: х = t2-1.
Слайд 14
Подставим это выражение в первое уравнение и новое
уравнение упростим
(t2-1)2+8(t2-1)+8=4(t2-1)t,
t4-2t2+1+8t2-8+8=4t3+4t,
t4-4t3+6t2-4t+1=0.
Последнее уравнение имеет корень t=1. Мало того, проверка
показывает, что значение t=1 является четырехкратным корнем этого уравнения. Тогда уравнение принимает вид (t-1)4=0. Если t=1, то х=0.
Ответ: 0.
Слайд 15
Функционально-графический метод
Пример 8.Решите уравнение:
Найдём
область определения D уравнения. Она совпадает с множеством всех решений системы неравенств
Решением первого неравенства является множество
, второго отрезок . Следовательно, область D состоит всего из двух точек -0 и 1. Значение х=0 не удовлетворяет уравнению, значение х=1- удовлетворяет.
Ответ: 1.