- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок презентация Периодичность тригонометрических функций
Содержание
- 2. Цели урокаЗнать: определение периодичности тригонометрических функций. Уметь: находить период тригонометрических функций.
- 3. Толкование в словаре Периодичность — это повторяемость (цикличность) явления через определенные промежутки времени. Смену дня и ночи, времён года, фаз Луны мы видим в повседневной жизни. Свет, звук, тепло, радиоволны, переменный электрический ток представляют собой колебательные, периодические процессы.Точно повторяющиеся движения называются периодическими.
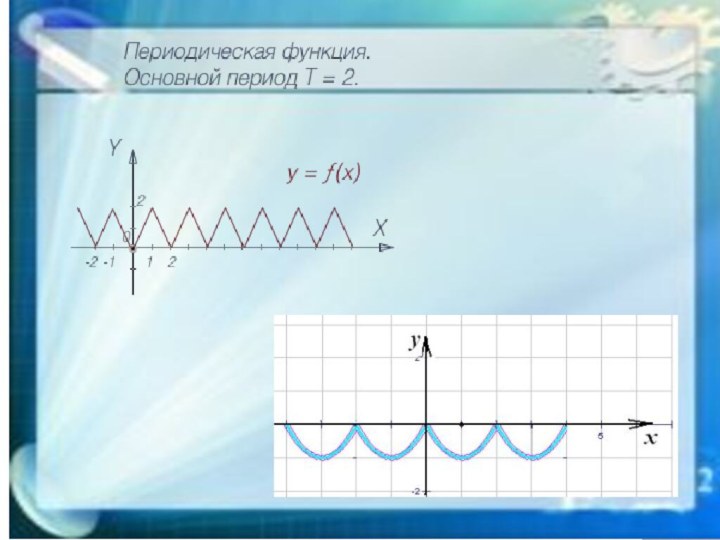
- 4. Определение периодической функции Функция периодическая, если она повторяется. Есть понятие периода функции - длина интервала повторения..
- 6. ОпределениеФункция у=f(x) называется периодической , если существует такое отличное
- 7. У периодической функции бесконечно много периодов, если
- 8. sin(x+2kπ)=sinx, k∈Z.cos(x+2kπ)=cosx,k∈Z.у=sinx, у=cosx — периодические функции с
- 9. Пример №1Найти основной период функции у =
- 10. Свойство 1.
- 11. Пример №2. Найти наименьший положительный период функций
- 12. Свойство 2.
- 13. Пример №3. Найти период функции
- 14. Проверь себя ! Стр. 12 №18, №19
- 15. Итог урока:Что нового вы узнали на уроке?
- 16. п. 2, стр.11 ; № 14- 15стр.39; №111.Домашнее задание:
- 17. Скачать презентацию
- 18. Похожие презентации
Цели урокаЗнать: определение периодичности тригонометрических функций. Уметь: находить период тригонометрических функций.
















Слайд 2
Цели урока
Знать: определение периодичности тригонометрических функций.
Уметь: находить
период тригонометрических функций.
Слайд 3
Толкование в словаре
Периодичность — это повторяемость (цикличность) явления через определенные промежутки времени.
Смену дня и ночи, времён года, фаз Луны мы
видим в повседневной жизни.
Свет, звук, тепло, радиоволны, переменный
электрический ток представляют собой
колебательные, периодические процессы.
Точно
повторяющиеся движения называются периодическими.
Слайд 4
Определение периодической функции
Функция периодическая, если она повторяется.
Есть понятие периода функции - длина интервала повторения..
Слайд 6
Определение
Функция у=f(x) называется периодической , если существует такое отличное от
нуля число Т, что для любого х из области
определения этой функции значения x + T и x – T также принадлежат области определения и выполняется двойное равенство f ( x - T) = f(x) = f(x + T) Т - период функции у=f(x)Слайд 7 У периодической функции бесконечно много периодов, если Т
период, то и 2Т и 3Т и 10Т тоже
периоды, вообще любое число вида: kT, где k- целое число.Наименьший положительный период называется основным периодом.