- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение производной для исследования функций
Содержание
- 2. Монотонность функцииУбывает на (-∞;x1], [x2;+∞)Возрастает на [х1; х2].Постоянна на [а;в]ухУ=f(x)x1х2ав
- 3. Исследование функции на возрастание
- 4. Исследование функции на убывание
- 5. Исследование функции на постоянство у
- 6. ЭКСТРЕМУМЫНеобходимое условие экстремумаЕсли Х0 – точка
- 7. СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ ИНТЕРВАЛОВ МОНОТОННОСТИ И ЭКСТРЕМУМОВХарактер изменения функции- 2 3+-+
- 8. А с и м п т о
- 9. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЁ
- 10. Наибольшее и наименьшее значение функции, непрерывной
- 11. Скачать презентацию
- 12. Похожие презентации

![Применение производной для исследования функций Монотонность функцииУбывает на (-∞;x1], [x2;+∞)Возрастает на [х1; х2].Постоянна на [а;в]ухУ=f(x)x1х2ав](/img/tmb/12/1187002/1c45e657a5e24d8ac9af67653e3323b8-720x.jpg)




Слайд 3
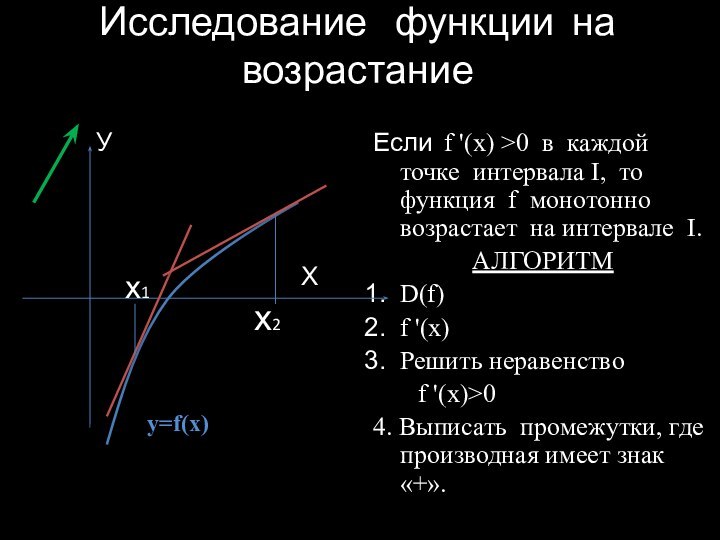
Исследование функции на возрастание
У
Х
Если f '(x) >0 в каждой точке интервала I, то функция f монотонно возрастает на интервале I.
АЛГОРИТМ
D(f)
f '(x)
Решить неравенство
f '(x)>0
4. Выписать промежутки, где производная имеет знак «+».
у=f(x)
х2
х1
Слайд 4
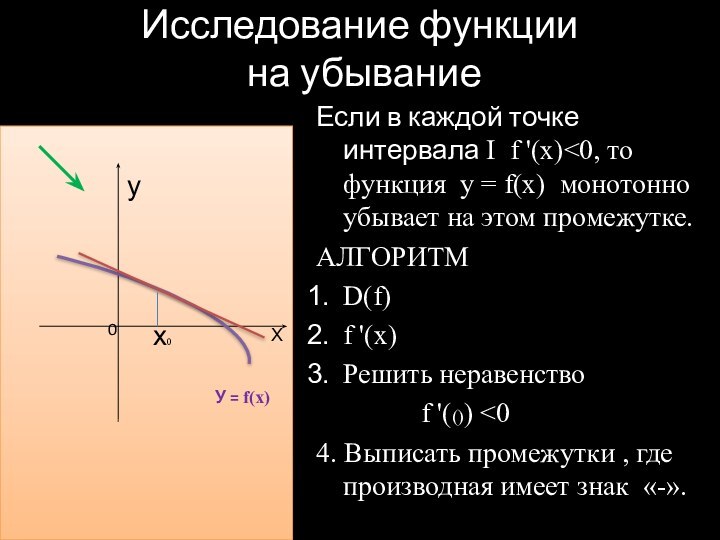
Исследование функции
на убывание
у
Если в каждой точке
интервала I f '(x)<0, то функция у = f(x) монотонно убывает на этом промежутке.АЛГОРИТМ
D(f)
f '(x)
Решить неравенство
f '(()) <0
4. Выписать промежутки , где производная имеет знак «-».
Х
0
х0
У = f(x)
Слайд 5
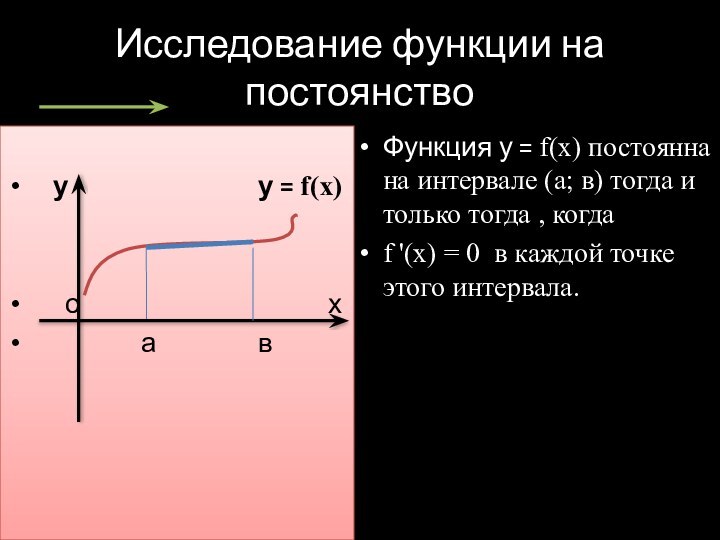
Исследование функции на постоянство
у
у = f(x)
о х
а в
Функция у = f(x) постоянна на интервале (а; в) тогда и только тогда , когда
f '(x) = 0 в каждой точке этого интервала.
Слайд 6
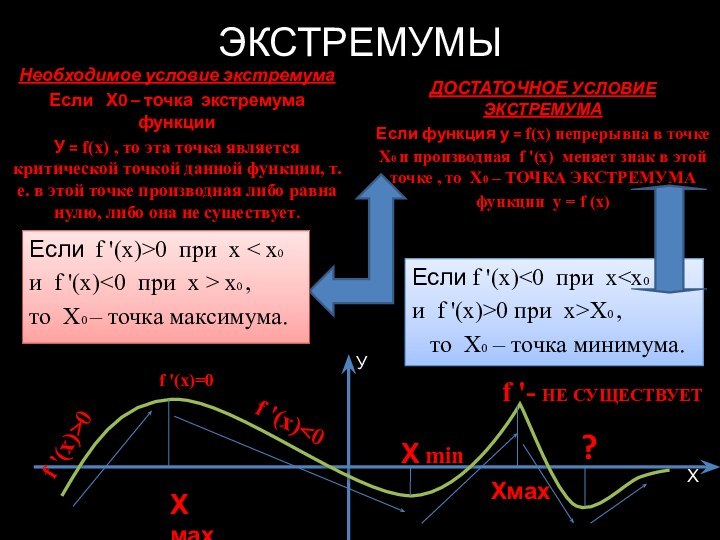
ЭКСТРЕМУМЫ
Необходимое условие экстремума
Если Х0 – точка экстремума
функции
У = f(x) , то эта точка является
критической точкой данной функции, т.е. в этой точке производная либо равна нулю, либо она не существует.Если f '(x)>0 при х < x0
и f '(x)<0 при х > x0 ,
то Х0 – точка максимума.
ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА
Если функция у = f(x) непрерывна в точке
Х0 и производная f '(x) меняет знак в этой точке , то Х0 – ТОЧКА ЭКСТРЕМУМА
функции у = f (x)
Если f '(x)<0 при х f '(x)>0 f '(x)=0 f '(x)<0 Х мах Х min f '- НЕ СУЩЕСТВУЕТ Хмах У Х ?
то Х0 – точка минимума.
Слайд 7 СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ ИНТЕРВАЛОВ МОНОТОННОСТИ И
ЭКСТРЕМУМОВ
Характер изменения функции
- 2
3
+
-
+
Слайд 8
А с и м п т о т
ы
Прямая у = кх +в называется асимптотой графика
функции у = f(x) , если расстояние от точки М графика функции до прямой у = кх + в стремиться к нулю при бесконечном удалении точки М.
Прямая х = а является вертикальной асимптотой графика функции
у = f(x), если lim f(x) = ∞
х→ а
Прямая у = в является горизонтальной асимптотой графика функции у = f(x), если
lim f(x)=b
х→∞
Прямая у = кх + в является наклонной асимптотой графика функции у = f(x), если lim f(x) =к
х →∞ х
lim ( f(x)─kx ) = b
Х→∞
х
У у = в
У= f(x)
у
0
а
Х = а
М.
.М
0 Х
У = f(x)
. М
у = кх + в
y=f(x)
У
0
Х
Слайд 9
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
И ПОСТРОЕНИЕ ЕЁ ГРАФИКА.
НАХОЖДЕНИЕ ОБЛАСТИ
ОПРЕДЕЛЕНИЯ И ОБЛАСТИ ЗНАЧЕНИЙ ФУНКЦИИ.
ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЧЕТНОСТЬ И
НЕЧЕТНОСТЬ.ИССЛЕДОВАНИЕ ФУНКЦИИ НА ПЕРИОДИЧНОСТЬ.
ОПРЕДЕЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ФУНКЦИИ С ОСЯМИ КООРДИНАТ И ИНТЕРВАЛОВ, ГДЕ ФУНКЦИЯ СОХРАНЯЕТ ЗНАК.
НАХОЖДЕНИЕ АСИМПТОТ ГРАФИКА ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ ТОЧЕК ЭКСТРЕМУМОВ ФУНКЦИИ.
ПОСТРОЕНИЕ ГРАФИКА.
Слайд 10
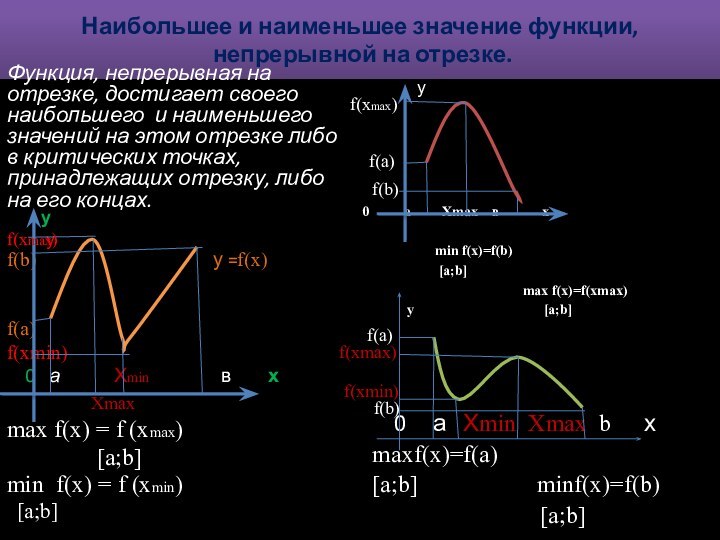
Наибольшее и наименьшее значение функции,
непрерывной на отрезке.
Функция,
непрерывная на отрезке, достигает своего наибольшего и наименьшего значений
на этом отрезке либо в критических точках, принадлежащих отрезку, либо на его концах.f(b) у =f(x)
f(a)
f(xmin)
0 а Хmin в х
Хmax
maх f(x) = f (xmax)
[a;b]
min f(x) = f (xmin)
[a;b]
0 а Хmax в х
min f(x)=f(b)
[a;b]
max f(x)=f(xmax)
у [а;b]
0 а Хmin Хmax b х
maxf(x)=f(a)
[а;b] minf(x)=f(b)
[a;b]
у
f(xmax)
у
f(b)
f(a)
f(xmax)
у
f(a)
f(xmax)
f(xmin)
f(b)