6) > 0
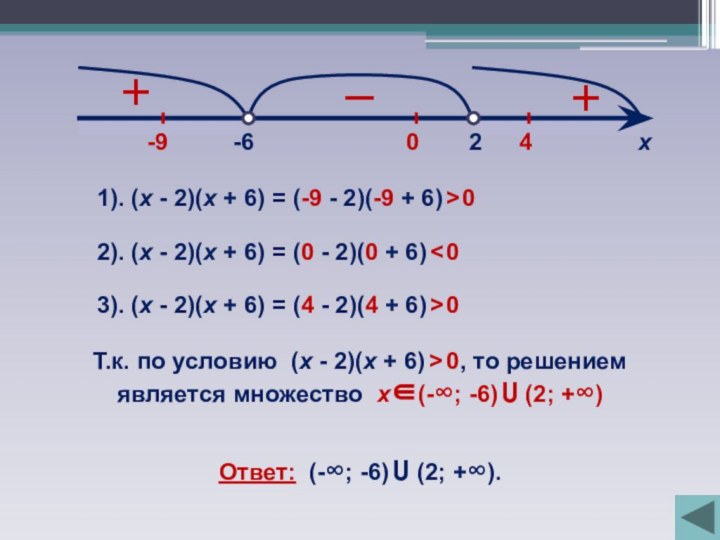
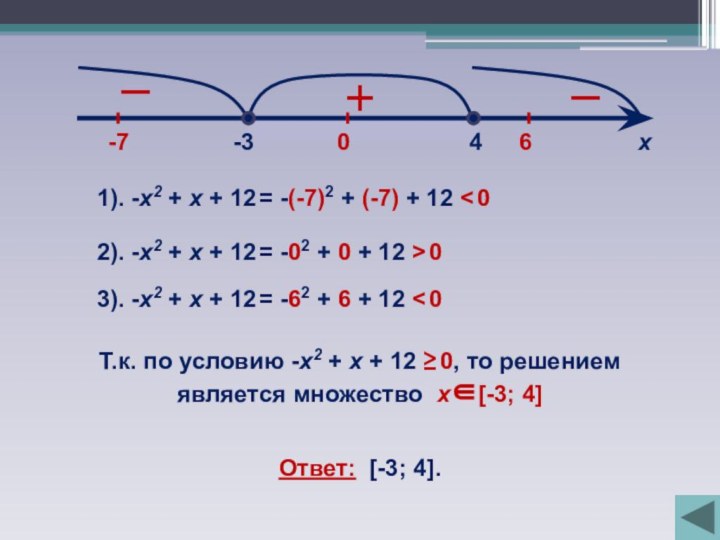
Найдём корни квадратного трехчлена из уравнения:
(х
– 2)(х + 6) = 0х1 = 2; х2 = -6
Отметим эти корни на числовой прямой:
2
-6
х
Получим три промежутка:
Определим знаки (х - 2)(х + 6) на каждом из полученных промежутков:
х – 2 = 0 или х + 6 = 0