Презентация на тему ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРА

мышления. В. П. Ермаков
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ
ПРИКЛАДНОГО

ХАРАКТЕРА



Преподаватель: Трофименко. М.В.

функции, имеющей на отрезке конечное число критических точек, нужно:
вычислить

значения функции во всех критических точках и на концах отрезка;

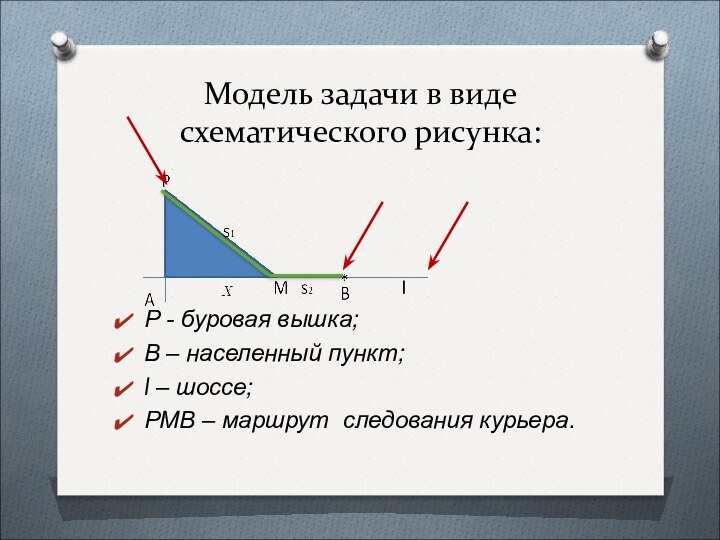
из полученных чисел выбрать наибольшее и наименьшее.

?

?

?

параметр (х), через который интересующую нас величину выразить как

функцию f(x);

средствами анализа найти наибольшее и наименьшее значение этой функции на некотором промежутке;

выяснить, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.

?

математической задачи;

интерпретация найденного решения.

ближайшей точки шоссе. С буровой надо направить курьера в

пункт, расположенный по шоссе в 15 км от упомянутой точки (считая шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь пункта?

Задача:

ближайшей точки шоссе?
На каком расстоянии находятся друг от друга

ближайшая точка от буровой вышки и пункт, куда надо отправить курьера?
Известна ли скорость курьера на велосипеде по полю?
Известна ли скорость курьера на машине по шоссе?
Известно ли, к какой точке шоссе надо ехать, чтобы достичь нужный пункт в кратчайшее время?

вышка;
В – населенный пункт;
l – шоссе;
РМВ – маршрут

следования курьера.

АМ, МВ, РМ.
Исследуемая величина – время, за которое курьеру

надо доехать до нужного пункта.
РА=9км, АВ=15км. vп = 8 км/ч, vш =10 км/ч.

треугольника РАМ выражаем:


3. путь S1(по полю), который курьер проходит

со скоростью v = 8 км/ч, а путь S2(по шоссе) – со скоростью v=10км/ч.

?

путь S2 за время

время, затраченное на путь S1 и S2,

в точке

Ответ: Курьеру надо ехать в точку, удаленную на

3 км от населенного пункта и на 12 км от шоссе, чтобы в кратчайшее время достичь населенного пункта

расстоянии 3 км от ближайшей точки берега А. Пассажир

лодки желает достигнуть села «В», находящегося на берегу на расстоянии 5 км от А. Лодка проплывает по 4 км/ч, а пассажир, выйдя из лодки, может в час пройти 5км. К какому пункту берега должна пристать лодка, чтобы пассажир достиг села «В» в кратчайшее время?

в 5км от прямолинейной дороги и в 13 км

от дома, стоящего у дороги. Скорость его передвижения в лесу 3км/ч, а по дороге 5 км/ч. Найдите наименьшее время, за которое он сможет прийти домой.