- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра логики
Содержание
- 2. Этапы развития логикиЛогика очень древняя наука.1-й этап
- 3. Этапы развития логики2-й этап – появление математической,
- 4. Формы мышленияЛогика – эта наука, изучающая законы
- 5. ПонятиеПонятие имеет две стороны: содержание и объем.
- 6. ПонятиеОбъем понятия – множество предметов, каждому из
- 7. УпражненияУпражнение 1. Приведите свои примеры понятий.Упражнение 21.
- 8. СужденияСуждение (высказывание, утверждение) – это форма мышления,
- 9. СуждениеВопросительные и восклицательные предложения не являются высказываниями,
- 10. УпражненияУпражнение 3. Объясните, почему следующие предложения не
- 11. УпражненияУпражнение 4. Какие из следующих высказываний являются
- 12. УмозаключениеУмозаключение – это форма мышления, с помощью
- 13. УмозаключениеНапример:1. Все металлы – простые вещества.Литий –
- 14. УпражнениеУпражнение 6. 1. Дано высказывание “Все углы
- 15. Алгебра высказыванийАлгебра высказываний была разработана для того,
- 16. В алгебре высказываний простым высказываниям ставятся в
- 17. Высказывания, как говорилось уже ранее, могут быть
- 18. Логические операцииЛогическая операция – способ построения сложного
- 19. Инверсия (от лат. inversion – переворачиваю) -
- 20. Конъюнкция (от лат. conjunction – связываю) -
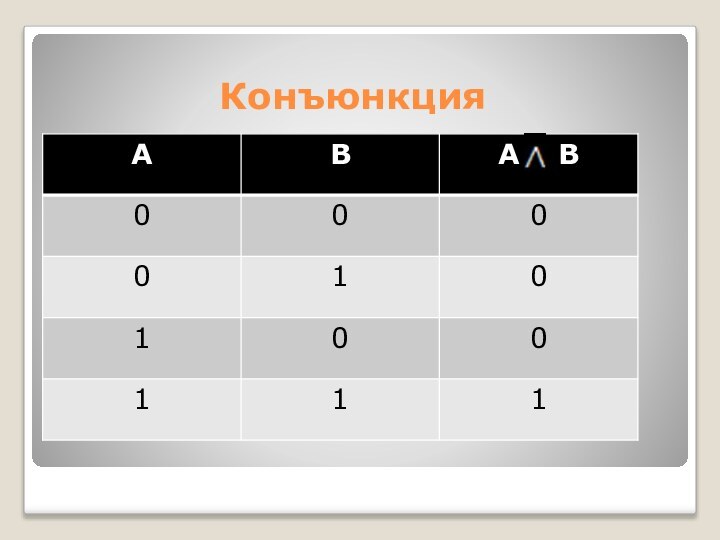
- 21. Конъюнкция
- 22. Дизъюнкция (от лат. disjunction – различаю) -
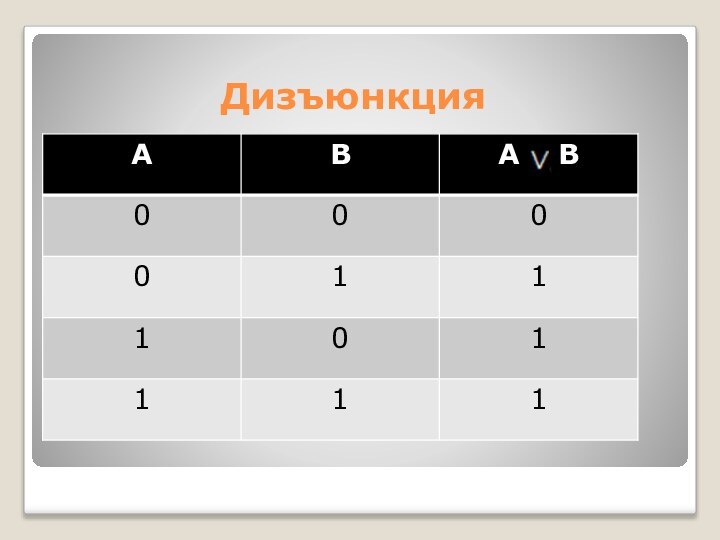
- 23. Дизъюнкция
- 24. Импликация (от лат. implication – тесно связывать)
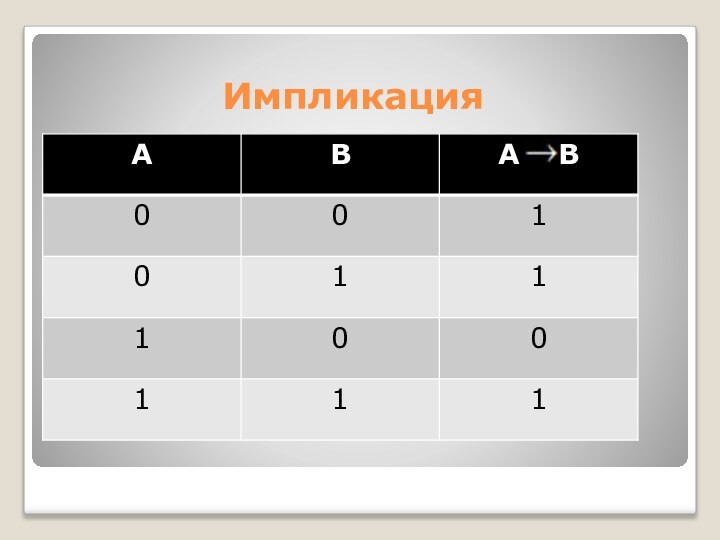
- 25. Импликация
- 26. Эквивалентность (от лат. equivalents – равноценность) -
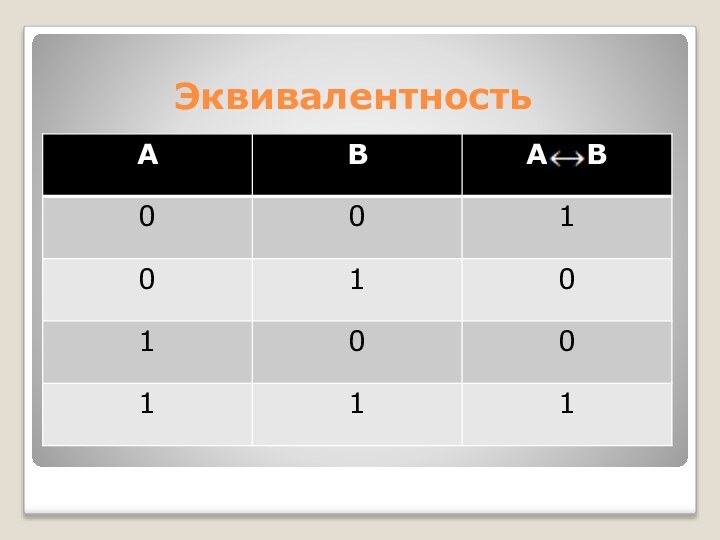
- 27. Эквивалентность
- 28. Упражнения Среди следующих высказываний укажите составные, выделите
- 29. Скачать презентацию
- 30. Похожие презентации
Этапы развития логикиЛогика очень древняя наука.1-й этап связан с работами ученого и философа Аристотеля (384-322 г.г. до н.э.). Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так

























Слайд 3
Этапы развития логики
2-й этап – появление математической, или
символической, логики. Основы ее заложил немецкий ученый и философ
Г.В. Лейбниц (1646-1716). Он сделал попытку построить первые логические исчисления, считал, что можно заменить простые рассуждения действиями со знаками, и привел соответствующие правила. Но он выдвинул только идею, а развил её окончательно англичанин Д. Буль (1815-1864).
Слайд 4
Формы мышления
Логика – эта наука, изучающая законы и
формы мышления; учение о способах рассуждений и доказательств.
Основными формами
мышления являются понятие, суждение, умозаключение. Понятие – это форма мышления, выделяющая существенные признаки предмета или класса предметов, позволяющих отличить их от других.
Например: компьютер, трапеция, портфель, ураганный ветер.
Слайд 5
Понятие
Понятие имеет две стороны: содержание и объем.
Содержание
понятия – совокупность существенных признаков, отраженных в этом понятии.
Например, содержание понятия персональный компьютер-это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.
Слайд 6
Понятие
Объем понятия – множество предметов, каждому из которых
принадлежат признаки, составляющие содержание понятий.
Например:
1. Объем понятия
город – это множество, состоящее из городов, носящих имя Москва, Одесса, Казань, Уфа, Нижнекамск и др.
2. Объем понятия персональный компьютер – совокупность существующих в мире персональных компьютеров.
Слайд 7
Упражнения
Упражнение 1. Приведите свои примеры понятий.
Упражнение 2
1. Перечислите
существенные признаки, составляющие содержание понятий: добродетель, истина, ложь. 2. Определите
объем понятий: столица России, столица, река.
Слайд 8
Суждения
Суждение (высказывание, утверждение) – это форма мышления, в
которой что-либо утверждается или отрицается о свойствах реальных предметов
и отношениях между ними.Высказывание может быть либо истинным, либо ложным, и может быть либо простым, либо составным (сложным).
Например:
1. Истинное высказывание: Буква “т” - согласная. 2. Ложное высказывание: Осень наступила, и грачи прилетели.
Слайд 9
Суждение
Вопросительные и восклицательные предложения не являются высказываниями, так
как в них ни чего не утверждается и не
отрицается.Например:
1. Уходя, гасите свет! 2. Кто хочет быть счастливым?
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков.
Например: 5>3, H2O+SO2=H2SO4.
Слайд 10
Упражнения
Упражнение 3. Объясните, почему следующие предложения не являются
высказываниями:
1. Какого цвета твой велосипед?
2. Число Х больше пяти?
3.
5Х-2
4. Посмотрите в окно.
5. Пейте томатный сок!
6. Вы были в музее?
7. Разность чисел 12 и Х равна 6.
Слайд 11
Упражнения
Упражнение 4. Какие из следующих высказываний являются истинными,
а какие ложными?
1. Город Москва – столица России.
2. Число
12 – простое.
3. 7*3=1.
4. 12<15.
5. Сканер – устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.
6. Клавиатура – устройство ввода информации.Упражнение 5. Приведите свои примеры истинных и ложных высказываний.
Слайд 12
Умозаключение
Умозаключение – это форма мышления, с помощью которой
из одного или нескольких суждений может быть получено новое
суждение.Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.
Слайд 13
Умозаключение
Например:
1. Все металлы – простые вещества.
Литий – металл.
Литий
– простое вещество.
2. Некоторые школьники – отличники.
Вовочка – школьник.
Вовочка
– отличник.
Слайд 14
Упражнение
Упражнение 6.
1. Дано высказывание “Все углы равнобедренного
треугольника равны”. Путем умозаключений получить высказывание “Этот треугольник равносторонний”. 2.
Оцените правильность следующего рассуждения: сидящий встал; кто встал, тот стоит; значит, сидящий стоит.
Слайд 15
Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы
можно было определять истинность или ложность составного высказывания, не
вникая в их содержание.Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно или ложно.
Слайд 16 В алгебре высказываний простым высказываниям ставятся в соответствии
логические переменные, обозначаемые прописными буквами латинского алфавита.
Например:
А= “Листва
на деревьях опадает осенью”.
В= “Земля прямоугольная”.Алгебра высказываний
Слайд 17 Высказывания, как говорилось уже ранее, могут быть истинными
или ложными. Истинному высказыванию соответствует значение логической переменной 1,
а ложному – значение 0 .Например:
А=1 В=0
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истина” (1) и “ложь” (0).
В алгебре высказываний над высказываниями можно производить логические операции, в результате которых получаются новые, составные (сложные) высказывания.
Алгебра высказываний
Слайд 18
Логические операции
Логическая операция – способ построения сложного высказывания
из данных высказываний, при котором значение истинности сложного высказывания
полностью определяется значениями истинности исходных высказываний.Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.
Слайд 19
Инверсия (от лат. inversion – переворачиваю) - отрицание.
Инверсия
логической переменной истина, если переменная ложна, и, наоборот, инверсия
ложна, если переменная истинна.Обозначается ¬А, читается не А.
Логические операции
Слайд 20 Конъюнкция (от лат. conjunction – связываю) - логическое
умножение.
Конъюнкция двух логических переменных истинна тогда и только тогда,
когда оба высказывания, истинны.Обозначается А В, читается А и В.
Логические операции
Слайд 22 Дизъюнкция (от лат. disjunction – различаю) - логическое
сложение.
Дизъюнкция двух логических переменных ложна тогда и только тогда,
когда оба высказывания ложны.Обозначается А В, читается А или В.
Логические операции
Слайд 24 Импликация (от лат. implication – тесно связывать) -
логическое следование.
Импликация двух логических переменных ложна тогда и только
тогда, когда из истинного основания следует ложное следствие.Обозначается А В, где А–условие
В - следствие.
Читается Если А, то В; Когда А, тогда В.
Логические операции
Слайд 26 Эквивалентность (от лат. equivalents – равноценность) - логическое
равенство.
Эквивалентность двух логических переменных истинна тогда и только тогда,
когда оба высказывания одновременно либо ложны, либо истинны.Обозначается А В, читается А тогда и только тогда, когда В.
Логические операции
Слайд 28
Упражнения
Среди следующих высказываний укажите составные, выделите в
них простые.
Число 456 трехзначное и четное.
Неверно, что Солнце движется
вокруг Земли.Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Луна – спутник Земли.
На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.
Если число оканчивается на 0, то оно делится на 10.
Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.
Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны.