Слайд 2
Пояснительная записка
Для изучения этой большой, сложной темы необходимо:
знать:
понятия тригонометрических функций для острого угла прямоугольного треугольника;
значения
тригонометрических функций для углов 30 , 45 и 60 ;
основные тригонометрические тождества;
уметь: использовать понятия, определения и формулы тригонометрии при упрощении и вычислении выражений с тригонометрическими функциями;
знать и уметь: определять обратные тригонометрические функции;
уметь решать тригонометрические уравнения и неравенства;
Слайд 3
Ну, что начнем изучение этой сложной темы!
Что такое
тригонометрия?
ТРИГОНОМетрия– (от греч. trigwnon – треугольник и metrew –
измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрических функций.
Слайд 4
Длина окружности вычисляется
по формуле С = 2πR
Длина полуокружности
равна πR
Повторение.
Слайд 5
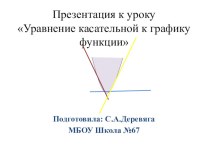
Центральный угол, опирающийся на дугу, длина которой равна
радиусу окружности, называется углом в 1 радиан.
0
R
R
R
1 рад
Длина
дуги равна R → угол 1 рад
Длина дуги равна πR → угол π рад
Развёрнутый угол равен π рад
π R
180º = π рад
360º = 2π рад
1 радиан =
1º =
Слайд 6
Если угол содержит α радиан, то его
градусная мера равна
Если угол содержит
α градусов, то его радианная мера равна
Слайд 9
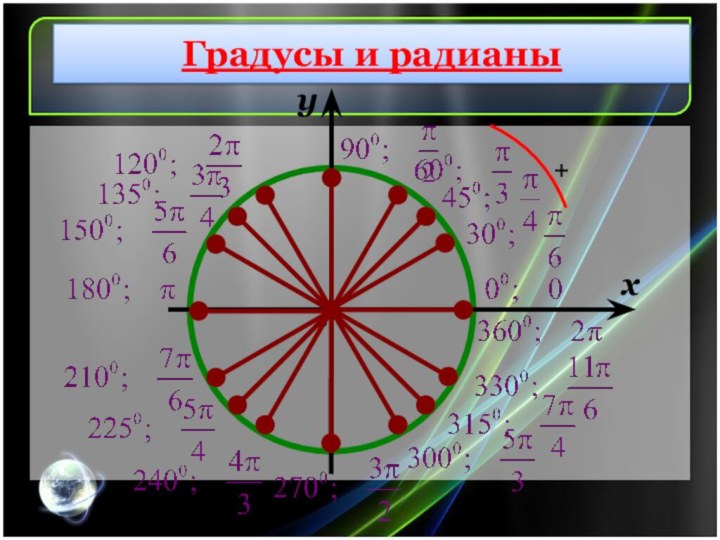
Выразите угол в радианах с помощью π:
45°=
150°=
90°=
360°=
30°=
270°=
135°=
60°=
180°=
- 210°=
-
720°=
Слайд 10
Найдите градусную меру угла, радианная мера которого равна:
18°
72°
540°
300°
108°
Слайд 12
Можно найти множество способов для
вычисления элементов прямоугольного треугольника, в котором опущена высота на
гипотенузу.
C
A
B
H
c
b
a
h
bc
ac
Катет прямоугольного треугольника есть среднее пропорциональное
для гипотенузы и проекции
катета на гипотенузу.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное
для проекций катетов на гипотенузу.
или
или
или
Слайд 14
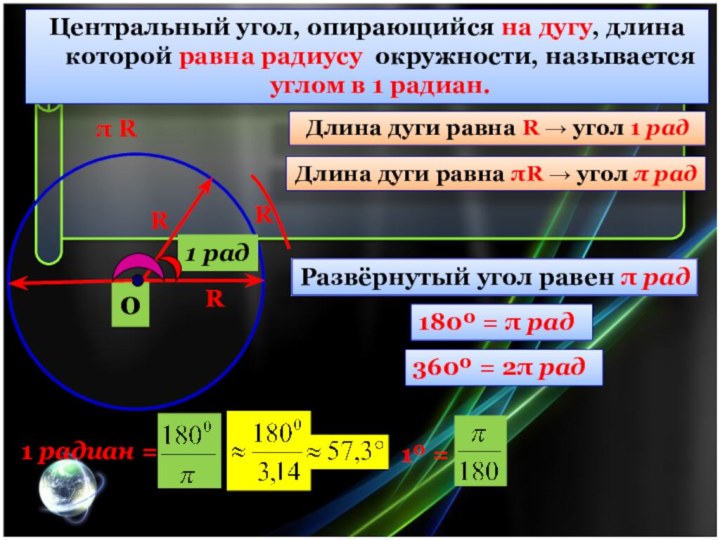
В треугольнике ABC АС=ВС, AB=20, sinBAC=0,7. Найдите высоту
AH.
1.
C
A
B
?
Слайд 15
C
A
B
6
?
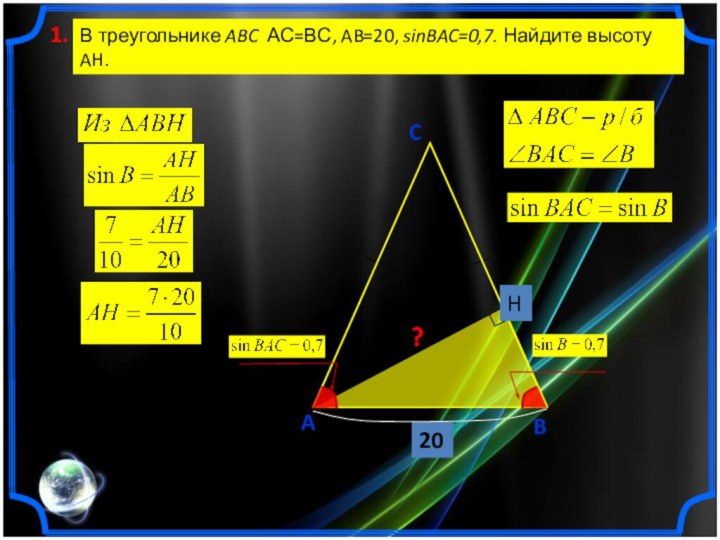
В треугольнике ABC АB=ВС, AC=6, sinACB=
.
Найдите высоту СH.
2.
Слайд 17
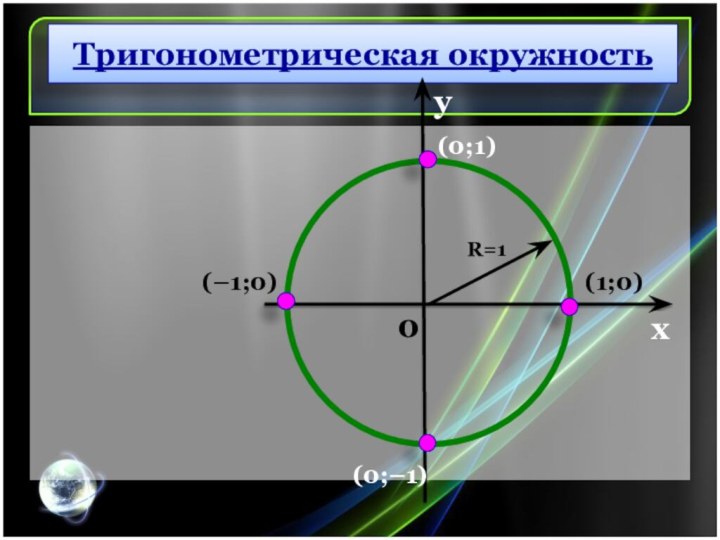
Тригонометрическая окружность
0
x
y
(0;1)
(–1;0)
(0;–1)
(1;0)
Слайд 18
0
x
y
Р(1;0)
М
М1
Тригонометрическая окружность
Слайд 19
0
x
y
00
1
1
–1
–1
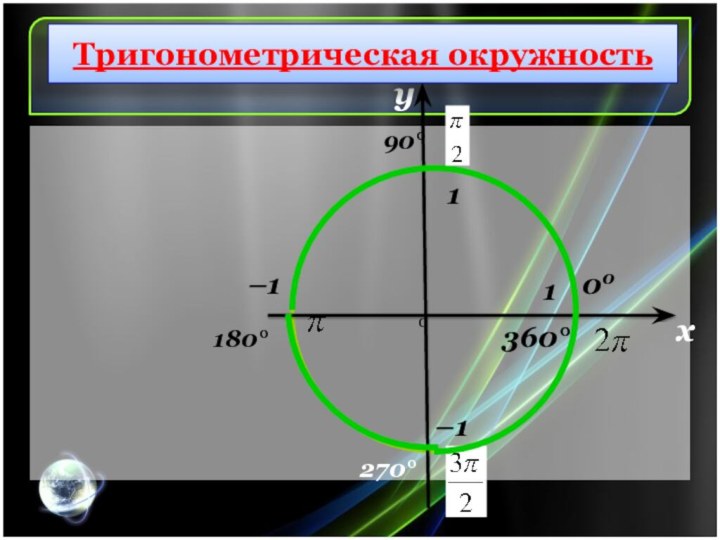
90°
180°
270°
360°
Тригонометрическая окружность
Слайд 22
0
x
y
00
1
1
–1
–1
90°
180°
270°
360°
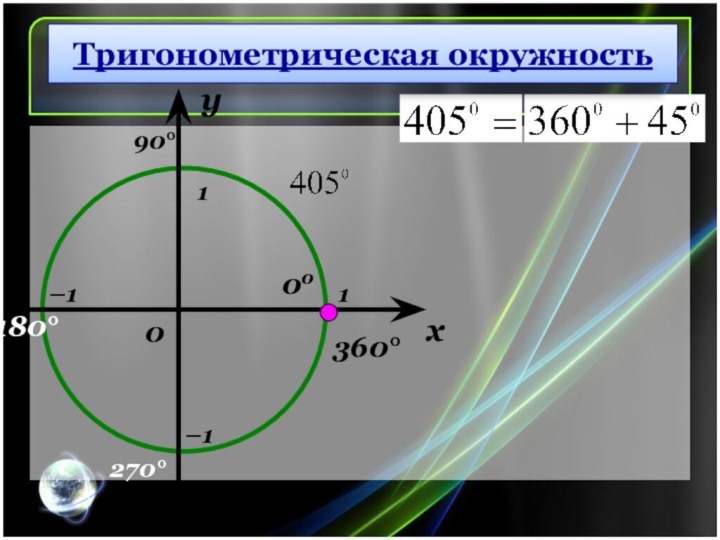
Тригонометрическая окружность
Слайд 23
0
x
y
00
1
1
–1
–1
Тригонометрическая окружность
Слайд 24
Значения синуса, косинуса, тангенса и котангенса
для некоторых
углов.
1
1
-1
-1
0
1
-1
-1
Слайд 25
y
x
1
π/3
5π/6
-π/4
4π/3
-π/2
7π/6
-3π/4
13π/6
-4π/3
-π
-π/6
2π
3π/4
-π/3
π/2
9π/4
Тригонометр:
отметь точку на единичной окружности
Слайд 26
y
x
1
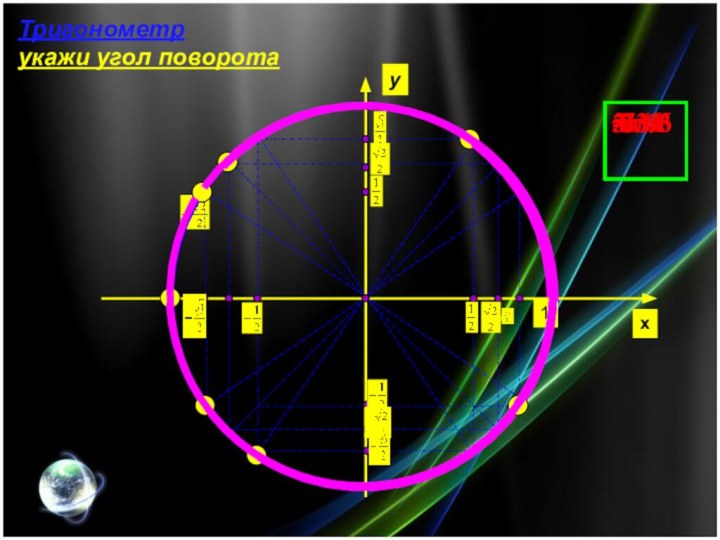
Тригонометр
укажи угол поворота
π/3
3π/4
-2π/3
-π
-π/6
5π/6
-5π/6
-7π/6
Слайд 27
Об измерении углов на практике
В качестве единицы измерения
плоских углов Международной системой единиц (СИ) принят радиан -
угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
Измерение углов в радианах на практике связано с значительными трудностями, так как ни один из современных угломерных приборов не имеет градуировки в радианах.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:
1 рад = 57°17׳45״ = 206 265″
1° = π/180 рад = 1,745329 × 10-2 рад;
1‘ = π /10800 рад = 2,908882 × 10-1 рад;
1” = π/648000 рад = 4,848137 × 10-6 рад.
Слайд 28
x
y
A
B
M
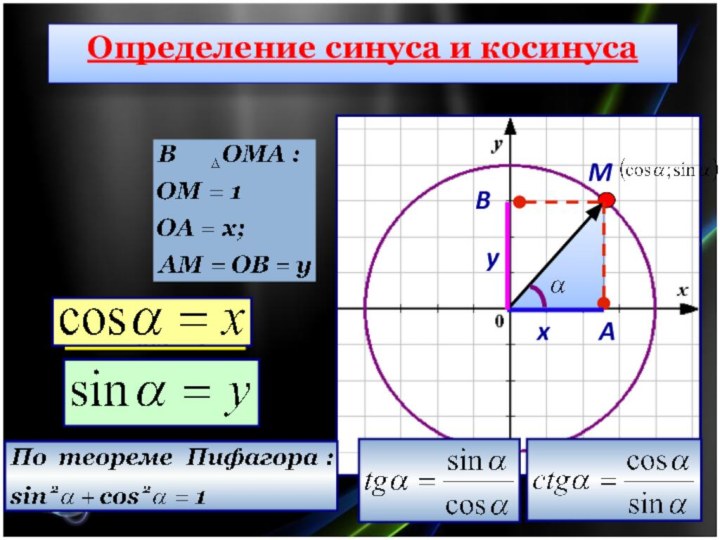
Определение синуса и косинуса
Слайд 29
х
у
0
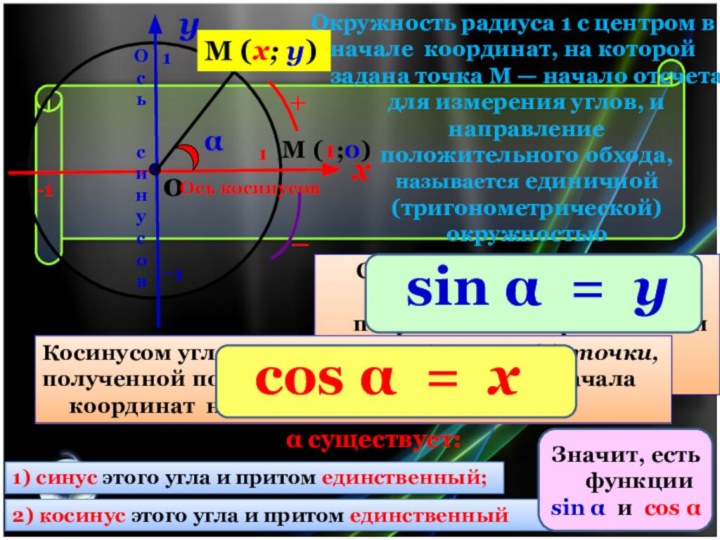
Окружность радиуса 1 с центром в
начале координат,
на которой задана точка М — начало отсчета для измерения углов, и
направление положительного обхода, называется единичной (тригонометрической) окружностью
Синусом угла α называется
ордината (у) точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α
М (x; y)
1
-1
1
̶ 1
α
М (1;0)
+
Косинусом угла α называется абсцисса (х) точки,
полученной поворотом точки (1; 0) вокруг начала координат на угол α
Для любого угла α существует:
1) синус этого угла и притом единственный;
2) косинус этого угла и притом единственный
̶
Ось
синусов
Ось косинусов
Слайд 30
x
y
1
-1
1
-1
0
(1;0)
(0;1)
( ̶ 1;0)
(0; ̶ 1)
Используя точку, соответствующую
углу α, запишите синус и косинус угла,
sin 00
= 0
cos 00 = 1
sin 900 = 1
cos 900 = 0
cos 1800 = –1
sin 1800 = 0
cos 2700 = 0
sin 2700 = –1
Слайд 31
M
C
K
Определение тангенса
Тангенсом угла α называется отношение
синуса угла α
к его косинусу.
Слайд 32
M
D
N
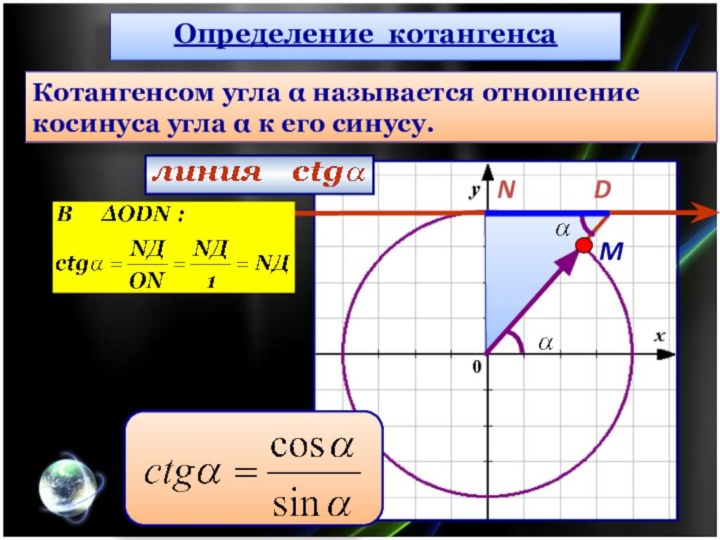
Определение котангенса
Котангенсом угла α называется отношение
косинуса угла α
к его синусу.
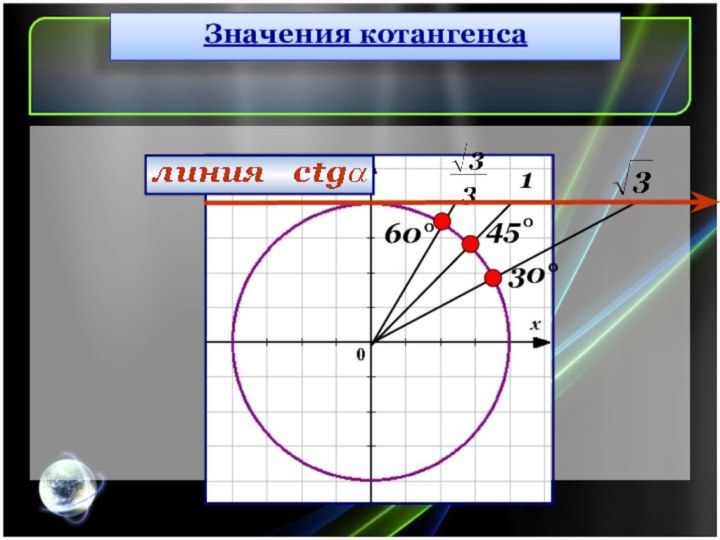
Слайд 33
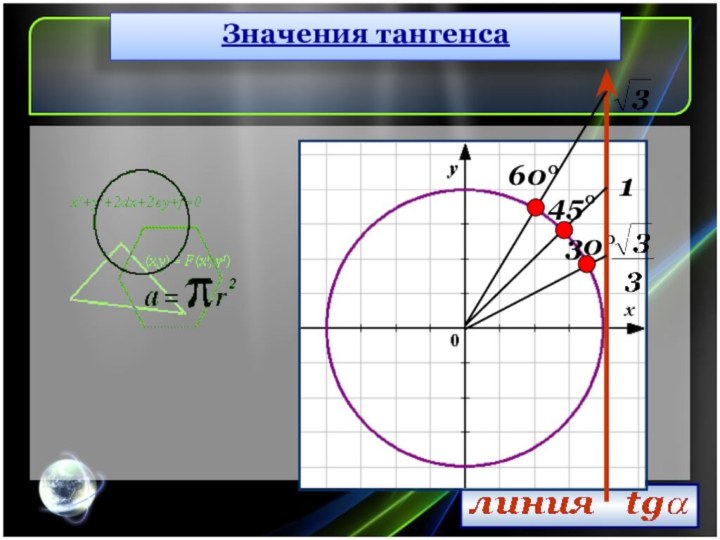
30°
45°
60°
Значения синуса и косинуса
Слайд 36
1
1
-1
-1
0
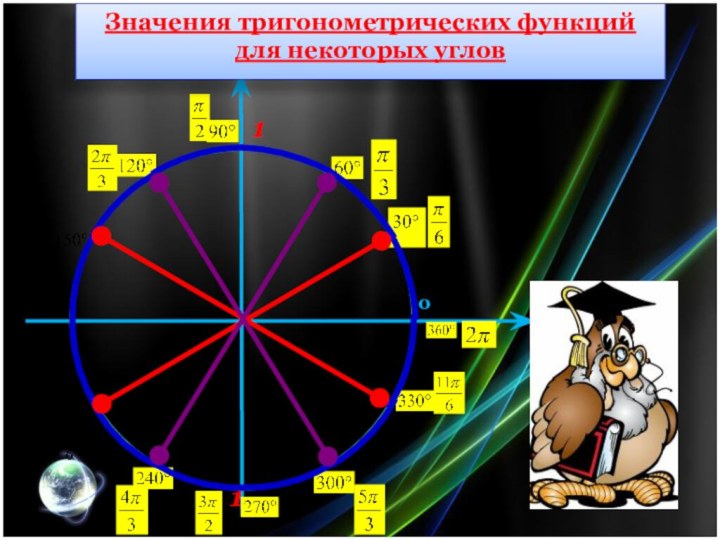
Значения тригонометрических функций для некоторых углов
Слайд 37
Значения тригонометрических функций для некоторых углов
1
1
-1
-1
0
Слайд 38
Значения тригонометрических функций для некоторых углов
1
1
-1
-1
0
Слайд 39
С
А
В
0
D
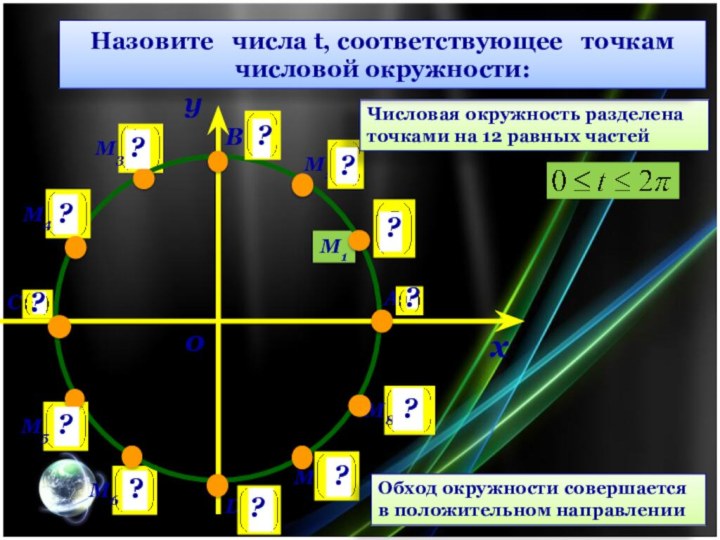
Числовая окружность разделена
точками на 12 равных частей
Обход
окружности совершается
в положительном направлении
?
?
?
?
?
?
?
?
?
?
?
?
y
x
Назовите числа t, соответствующее
точкам числовой окружности:
Слайд 40
y > 0
y < 0
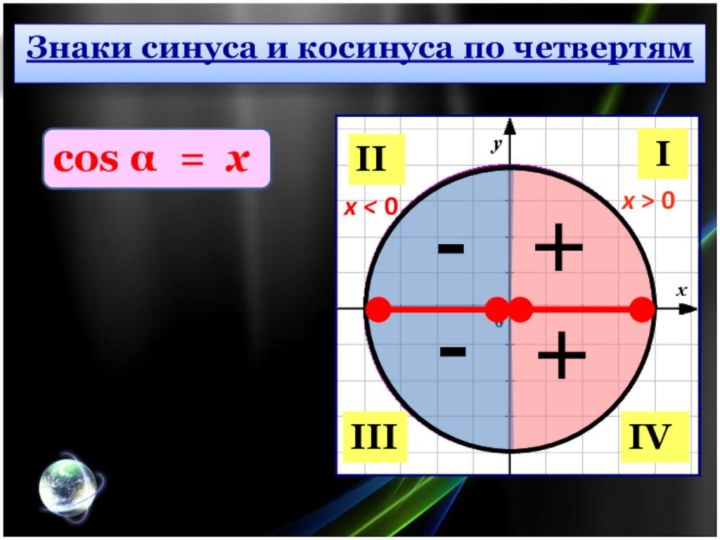
Знаки синуса и косинуса
по четвертям
Слайд 41
Знаки синуса и косинуса по четвертям
x > 0
x
Слайд 42
I
II
III
IV
sin α > 0
cos α > 0
sin α > 0
cos α < 0
sin
α < 0
cos α < 0
sin α < 0
cos α > 0
Знаки синуса и косинуса по четвертям
tg α > 0
сtg α > 0
tg α > 0
сtg α > 0
tg α 0
сtg α 0
tg α 0
сtg α 0
Слайд 43
sin a
–
+
+
+
+
+
+
–
–
–
–
–
cos a
tg a
x
1
–1
1
–1
Знаки тригонометрических функций
Слайд 44
х
у
0
A (x; y)
1
-1
1
̶ 1
α
Это основное тригонометрическое тождество
Для любого угла α справедливы неравенства
или
Слайд 46
Посчитаем устно! Устный счет – «ум в порядок
приводит»!
cos 300
cos 1800
sin 450
cos 900
tg 300
tg 00
cos 2700
sin 3600
cos
3000
sin 1500
tg 1200
Слайд 47
Дано: sin α = /3
α четверти
3
?
cos α =
/3
tg α = /
ctg α = /
По заданному значению
функции найдите значения остальных тригонометрических функций:
А, слабо решить задачу?
Слайд 50
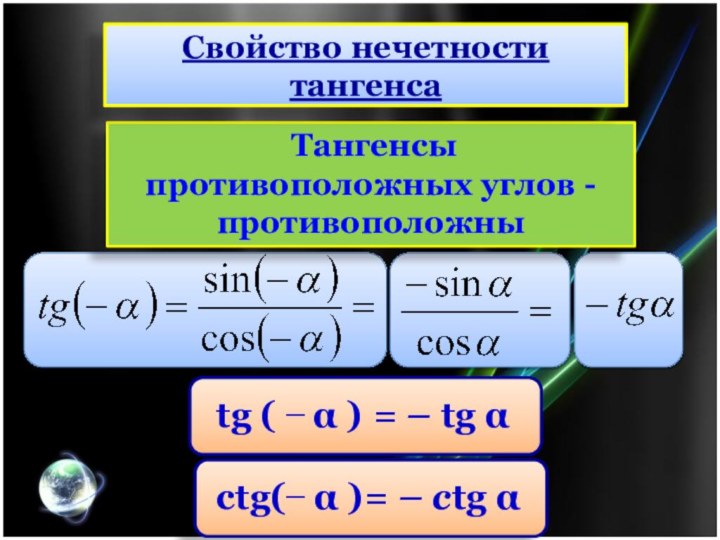
Тангенсы противоположных углов - противоположны
Свойство нечетности тангенса
Слайд 51
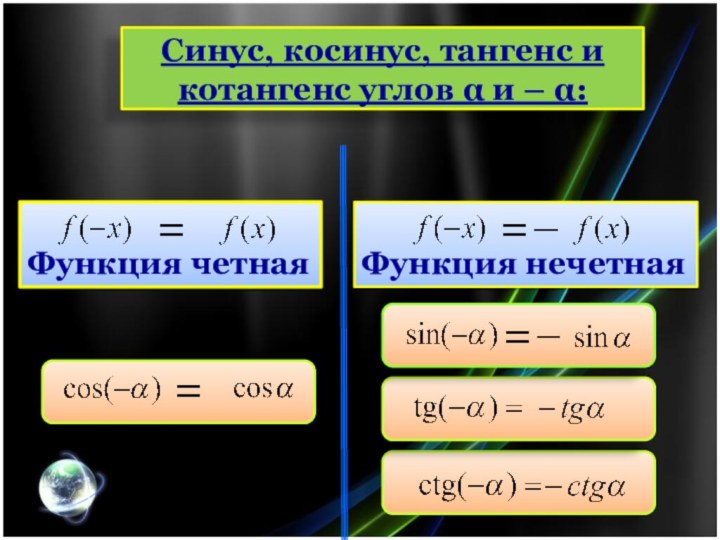
Синус, косинус, тангенс и котангенс углов и
– :
Слайд 52
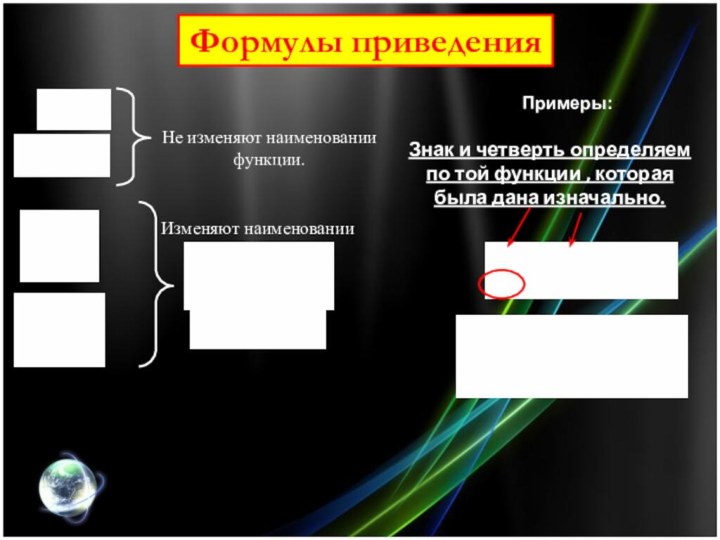
Формулы приведения
Изменяют наименовании функции:
Не изменяют наименовании функции.
Примеры::
Знак и
четверть определяем по той функции , которая была дана
изначально.
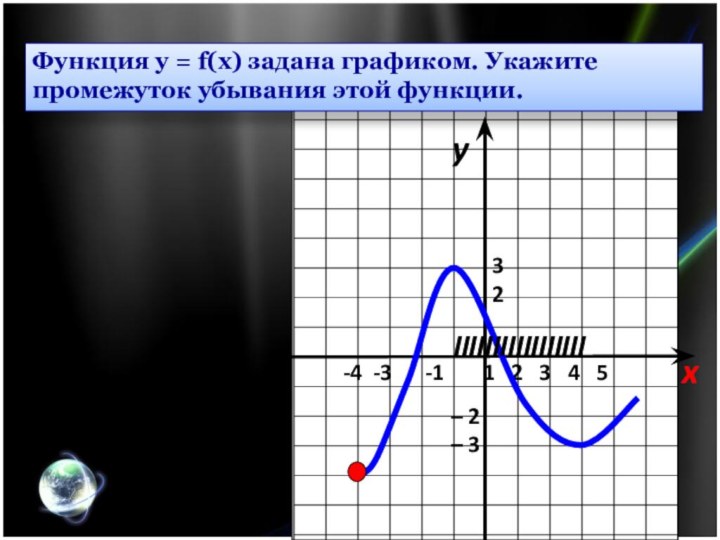
1 2 3 4 5
IIIIIIIIIIIII
–
2
– 3
3
2
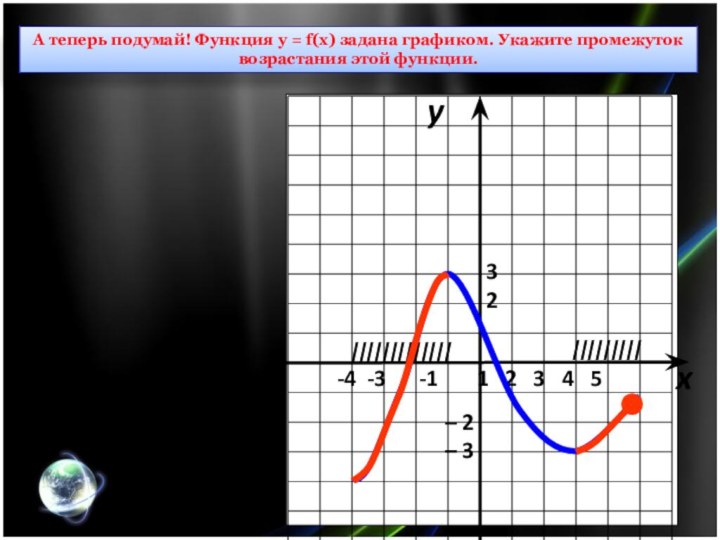
А теперь подумай! Функция у = f(x) задана графиком. Укажите промежуток возрастания этой функции.
IIIIIIIII
1 2 3 4 5
IIIIIIIIIIIIIIIII
–
2
– 3
3
2
Функция у = f(x) задана графиком. Укажите промежуток убывания этой функции.
Слайд 56
x0
O
x
y
-1
x1
x2
x3
x4
x5
x6
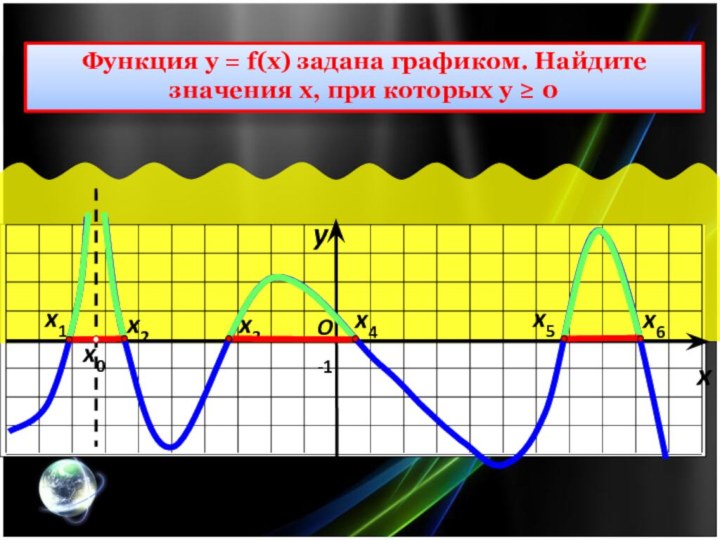
Функция у = f(x) задана графиком. Найдите значения
х, при которых у ≥ 0
Слайд 57
O
a
y
-1
x1
x2
x3
x4
x5
x6
b
Функция у = f(x) задана графиком. Найдите значения
х, при которых у < 0
x0
Слайд 58
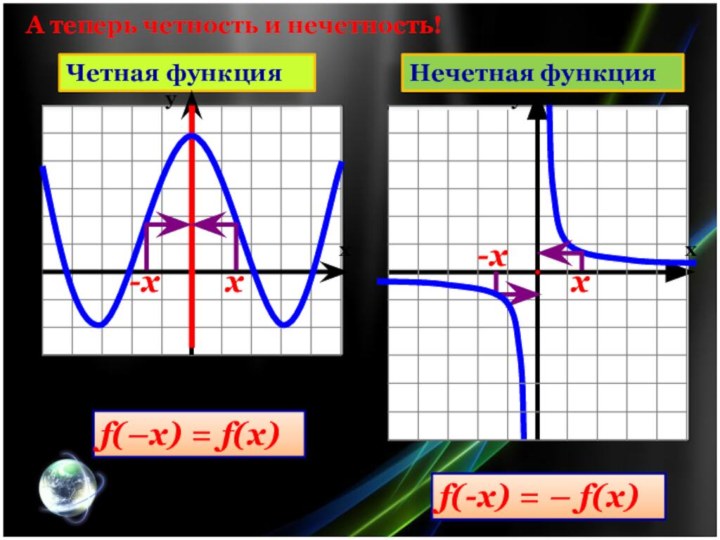
Четная функция
х
у
f(–x) = f(x)
-x
x
f(-x) = – f(x)
х
у
-x
x
Нечетная
функция
А теперь четность и нечетность!
Слайд 59
2
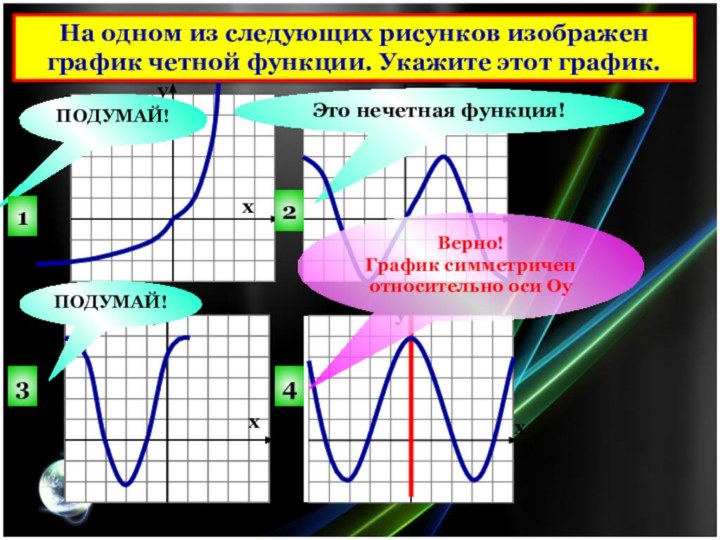
На одном из следующих рисунков изображен график четной
функции. Укажите этот график.
х
у
х
у
х
у
х
у
Это нечетная функция!
Верно!
График симметричен относительно
оси Оу
ПОДУМАЙ!
1
ПОДУМАЙ!
4
3
Слайд 60
На одном из следующих рисунков изображен график нечетной
функции. Укажите этот график.
3
4
2
1
ПОДУМАЙ!
у
х
х
х
х
у
у
Это четная функция!
у
ПОДУМАЙ!
Верно!
График симметричен относительно
точки О
Слайд 61
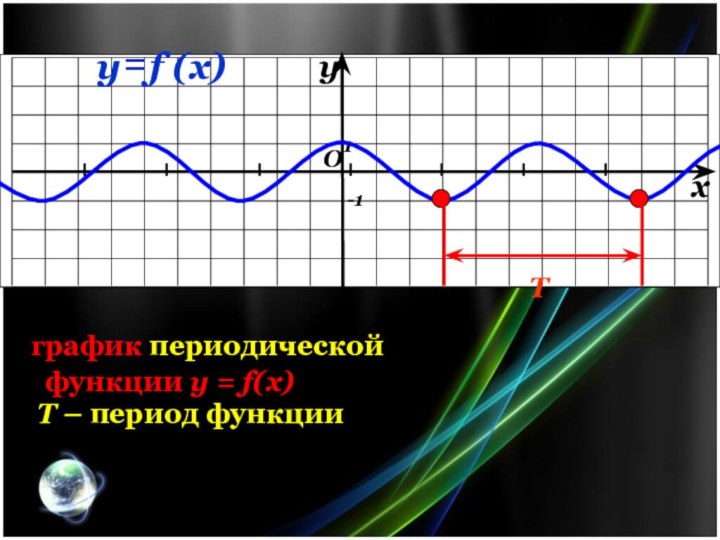
Функция называется периодической, если существует такое число Т
0, что для любого х из области определения этой
функции выполняется равенство:
число T называют периодом функции y = f(x)
f (x – T) = f(x) = f (x + T)
Свойства функции
I
I I I I I I
O
x
y
-1
1
график периодической
функции y = f(x)
T
T – период функции
Слайд 63
Периодичность sina, cosa, tga и ctga.
Слайд 65
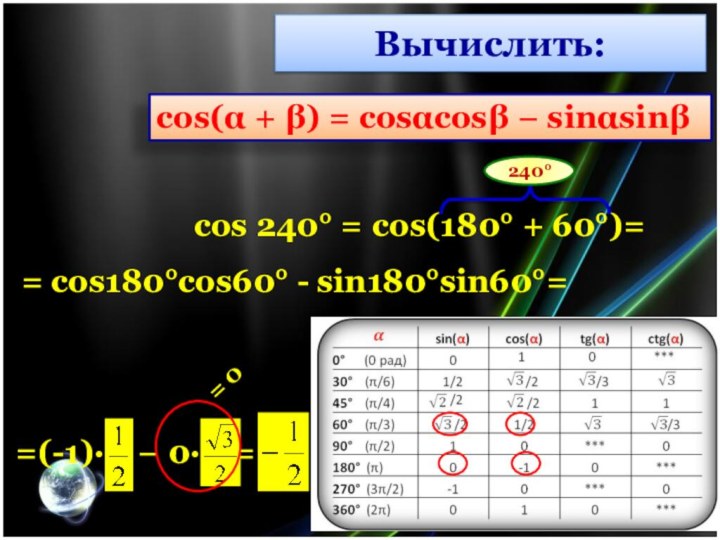
cos 240° =
cos(180° + 60°)=
240°
= cos180°cos60° - sin180°sin60°=
=(-1)·
− 0· =
= 0
Вычислить:
cos(α + β) =
cosαcosβ − sinαsinβ
Слайд 66
cos 3α cosα – sinα sin3α =
cosxcosy – sinxsiny =cos(x + y)
= cos(3α +
α) =
cos 4α.
cosxcosy + sinxsiny = cos(x − y)
− 1
Упростить выражение:
Слайд 68
Формулы преобразования произведения функций в сумму и обратно
Слайд 69
Формулы преобразования суммы функций в произведение и обратно
Слайд 70
Уравнение есть равенство, которое еще не является истинным,
но которое стремятся сделать истинным, не будучи уверенными, что
этого можно достичь. А Фуше
А теперь тригонометрические уравнения! Вспомним, что изучали ранее.
Тригонометр, то есть отметим точку на тригонометрической окружности и укажем угол поворота.
Слайд 71
y
x
1
Тригонометр
укажи угол поворота
π/3
3π/4
-2π/3
-π
-π/6
5π/6
-5π/6
-7π/6
Слайд 72
Вы в курсе, что тригонометрические уравнения могут быть
моделями задач физики, астрономии, сейсмологии, архитектуры, экономики, компьютерной графики
и многих других сфер жизни и деятельности человека.
Учимся решать как элементарные, так и достаточно сложные тригонометрические уравнения.
Слайд 73
4) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и
уметь отмечать их на числовой окружности.
1) уметь отмечать точки
на числовой
окружности;
3) знать свойства основных тригонометрических функций;
Чтобы успешно решать простейшие тригонометрические уравнения, необходимо:
2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности;
Слайд 74
y
x
1
Решение уравнения вида cos t = a
a
Ответ:
Cos
Слайд 75
3
2
1
π/3
-π/3
½
Решим уравнение:
x = 2n , nZ
Решений нет
x1=
π/3+2n , nZ
x2=–π/3+2n , nZ
cos x=1,5
cos x=1
cos x=0,5
Слайд 76
π
0
arccos а
а
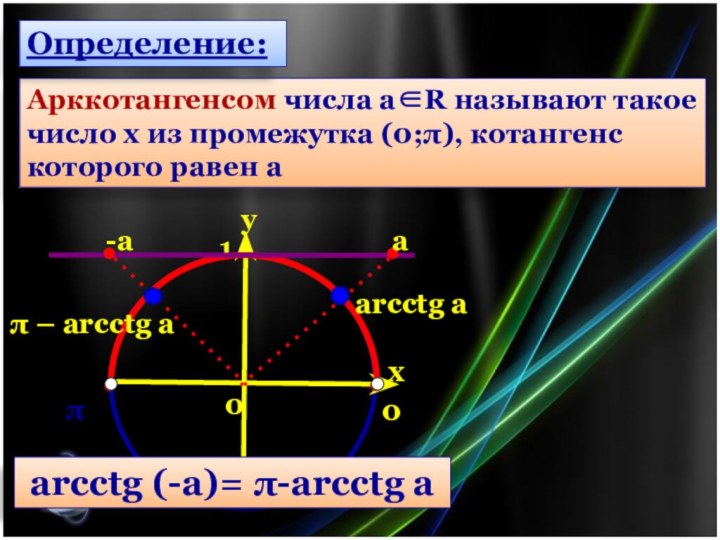
arccos (-a)= π -arccos a
–а
π – arccos
a
Определение:
Арккосинусом числа а [-1;1 ] называют такое число х
из промежутка [0;π ], косинус которого равен а
Слайд 77
1
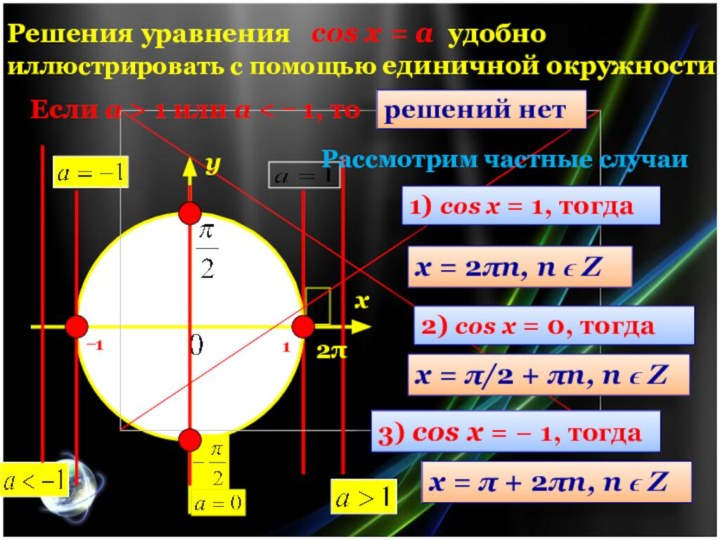
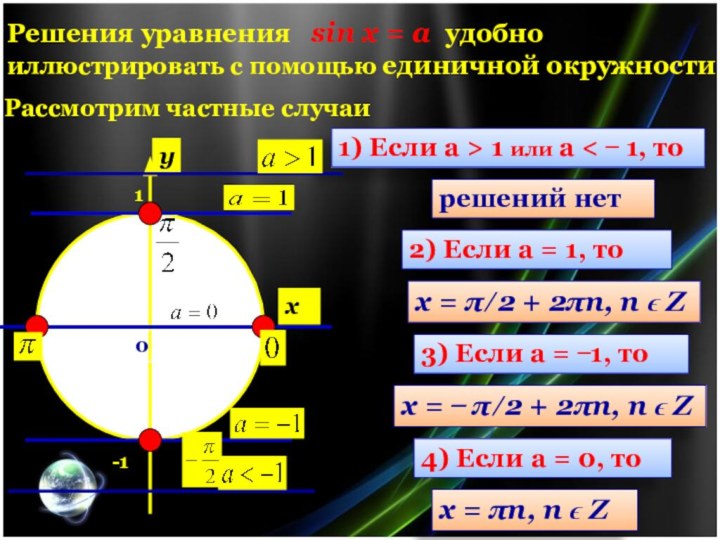
Решения уравнения cos х = a удобно
иллюстрировать с помощью единичной окружности
Рассмотрим частные случаи
Если a
> 1 или a < ̶ 1, то
решений нет
1) cos х = 1, тогда
х = 2πn, n ϵ Z
2) cos х = 0, тогда
х = π/2 + πn, n ϵ Z
3) cos х = − 1, тогда
х = π + 2πn, n ϵ Z
y
x
̶ 1
2π
Слайд 78
Вы должны знать:
1) Если │а │> 1, то
решений нет.
2) Частные случаи:
3) Общая формула для
Слайд 79
3
2
1
π/6
5π/6
½
x = π/2+2n , nZ
Решений нет
x1= π/6+2n
, nZ
x2=5π/6+2n , nZ
Решим уравнение:
sin x=1,5
sin x=1
sin x=0,5
Слайд 80
arcsin а
а
arcsin (-a)= –arcsin a
-а
-arcsin а
Арксинусом числа а
[-1;1 ] называют такое число х из промежутка
[–π/2;π/2], синус которого равен а
Определение:
Слайд 81
1) Если a > 1 или a
̶ 1, то
y
x
1
-1
решений нет
2) Если а = 1,
то
Рассмотрим частные случаи
Решения уравнения sin х = a удобно иллюстрировать с помощью единичной окружности
х = π ̸ 2 + 2πn, n ϵ Z
3) Если а = ̶ 1, то
х = ̶ π ̸ 2 + 2πn, n ϵ Z
4) Если а = 0, то
х = πn, n ϵ Z
0
Слайд 82
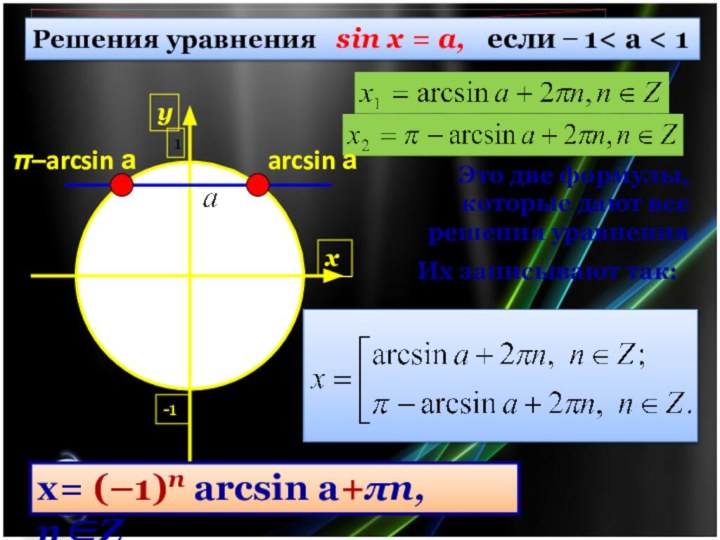
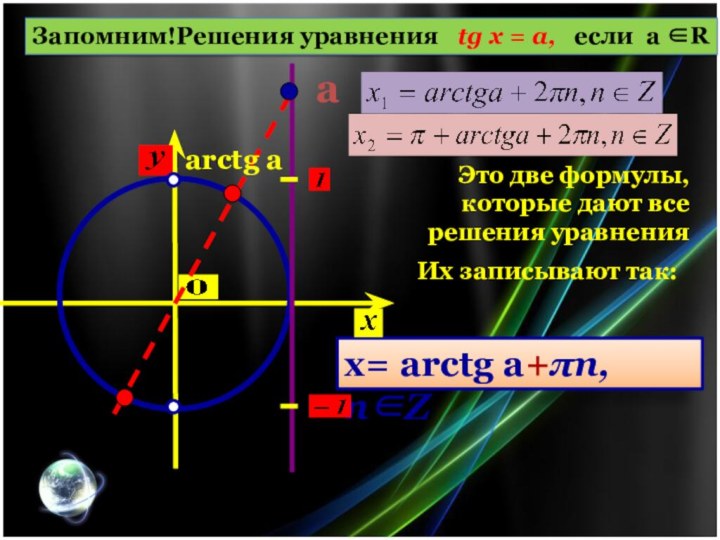
Это две формулы, которые дают все решения уравнения
Их
записывают так:
Решения уравнения sin х = a,
если ̶ 1< a < 1
х= (–1)n arcsin а+n, nZ
arcsin а
–arcsin а
Слайд 83
1) Если │а │> 1, то решений нет.
2)
Частные случаи:
3) Общая формула для
А это стоит запомнить!
Слайд 84
Потренируемся в решении уравнений?
Слайд 85
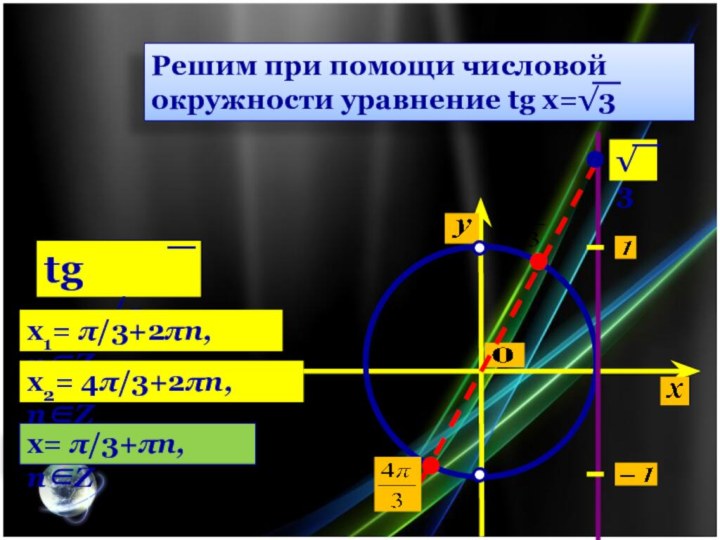
Решим при помощи числовой окружности уравнение tg х=3
tg
х=3
х1= /3+2n, nZ
х2= 4/3+2n, nZ
х= /3+n, nZ
Слайд 86
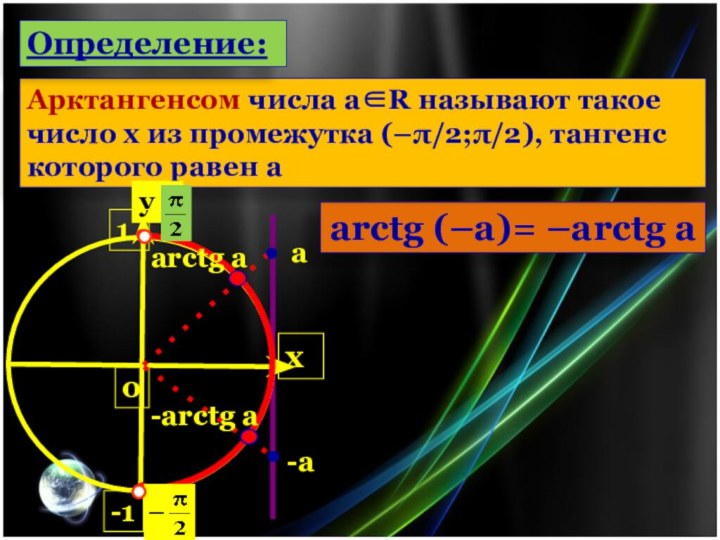
arctg (–a)= –arctg a
Арктангенсом числа аR называют такое
число х из промежутка (–π/2;π/2), тангенс которого равен а
Определение:
arctg
a
а
-а
-arctg a
Слайд 87
Это две формулы, которые дают все решения уравнения
Их
записывают так:
Запомним!Решения уравнения tg х = a,
если a R
х= arctg а+n, nZ
а
arctg a
Слайд 88
Арккотангенсом числа аR называют такое число х из
промежутка (0;π), котангенс которого равен а
Определение:
π
у
х
0
1
0
-а
arcctg a
а
π – arcctg
a
arcctg (-a)= π-arcctg a
Слайд 89
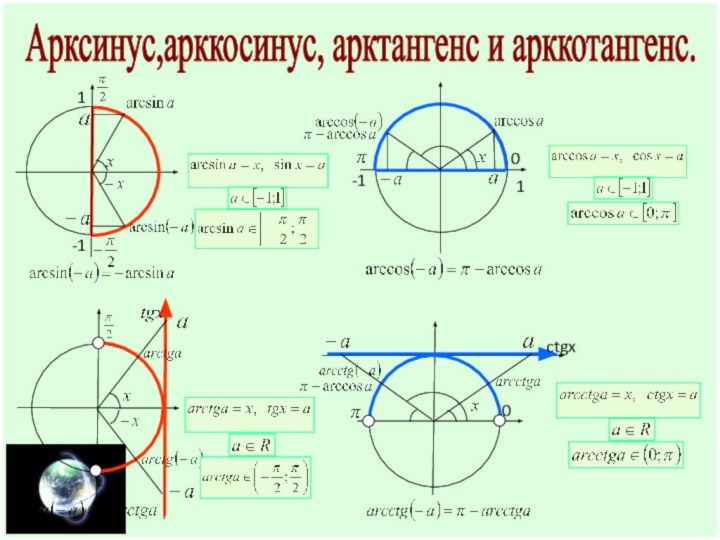
Арксинус,арккосинус, арктангенс и арккотангенс.
0
0
-1
1
-1
1
ctgx
Слайд 90
Это две формулы, которые дают все решения уравнения
Их
записывают так:
Решения уравнения сtg х = a,
если a R
х= arсctg а+n, nZ
сtg х=а
arcctg a
а
Слайд 92
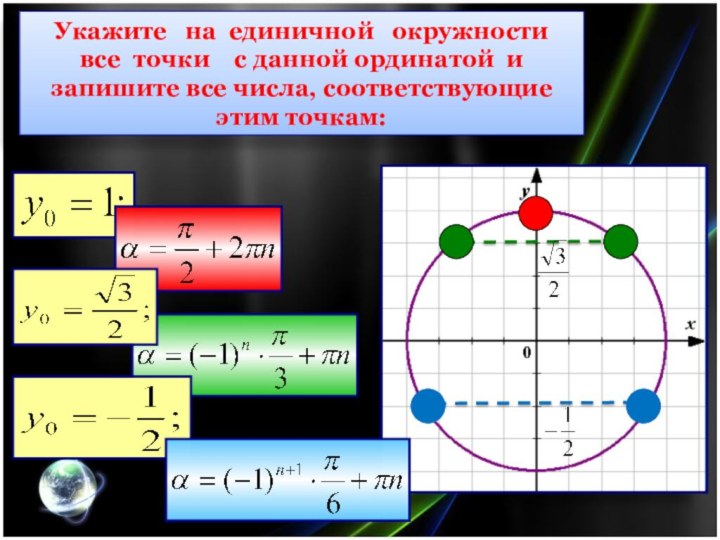
Укажите на единичной окружности все
точки с данной ординатой и запишите все числа,
соответствующие этим точкам:
Слайд 93
Укажите на единичной окружности все
точки с данной ординатой и запишите все числа,
соответствующие этим точкам:
Слайд 94
Решить уравнение:
В ответе запишите наибольший отрицательный корень
1
В ответе
запишите наибольший отрицательный корень
2
В ответе запишите наибольший отрицательный корень
3
Слайд 95
На Оу отмечаем значение
и соответствующие точки на окружности
Выделяем
нижнюю часть окружности (обход совершаем против
часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Ответ:
kZ
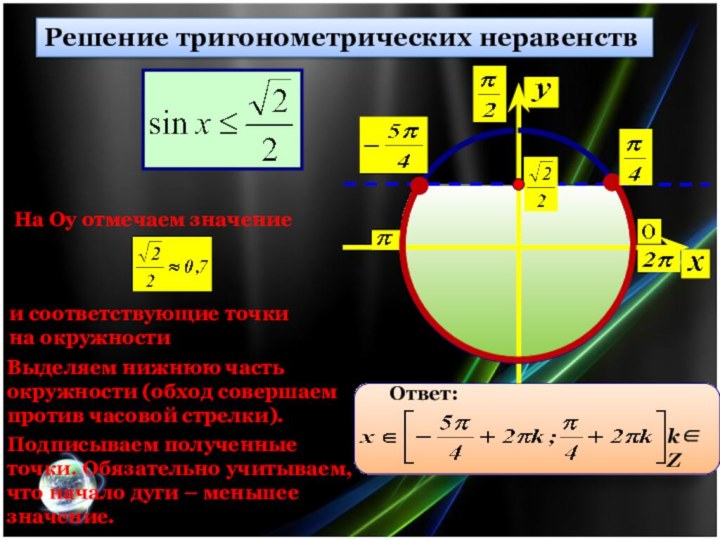
Решение тригонометрических неравенств
Слайд 96
Решение тригонометрических неравенств
На Оу отмечаем значение
и соответствующие точки
на окружности
Выделяем верхнюю часть окружности (обход
совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Ответ:
kZ
Слайд 97
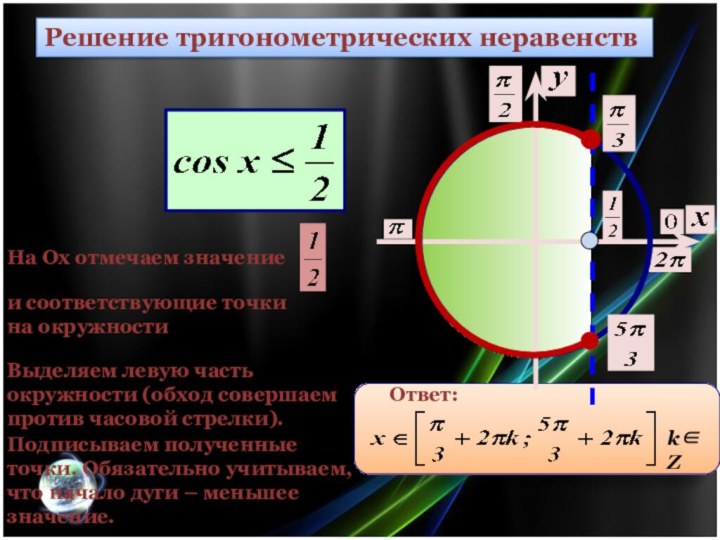
Решение тригонометрических неравенств
На Ох отмечаем значение
и соответствующие точки
на окружности
Выделяем правую часть окружности (обход
совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Ответ:
kZ
Слайд 98
Решение тригонометрических неравенств
kZ
На Ох отмечаем значение
и соответствующие точки
на окружности
Выделяем левую часть окружности (обход
совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Ответ:
Слайд 99
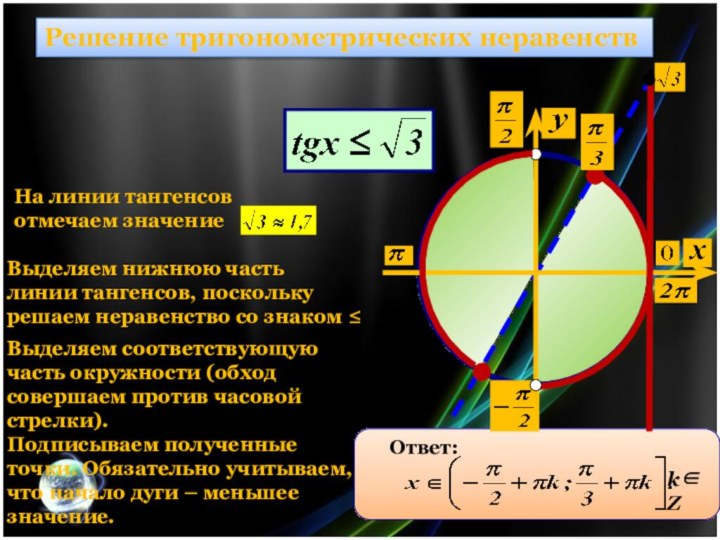
kZ
Ответ:
На линии тангенсов отмечаем значение
Выделяем нижнюю часть
линии тангенсов, поскольку решаем
неравенство со знаком ≤
Выделяем соответствующую часть окружности (обход совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Решение тригонометрических неравенств
Слайд 100
Решение тригонометрических неравенств
kZ
Ответ:
На линии тангенсов отмечаем значение 1.
Выделяем
верхнюю часть линии тангенсов, поскольку
решаем неравенство со знаком ≥
Выделяем соответствующую часть окружности (обход совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Слайд 101
Основные методы решения тригонометрических уравнений
Метод введения новой переменной
Метод
разложения на множители
Функционально - графический
Слайд 102
Тригонометрические уравнения, приводимые к алгебраическим уравнениям относительно одной
тригонометрической функции
Слайд 103
Тригонометрические уравнения, решаемые путем преобразований тригонометрическими формулами
Слайд 104
Тригонометрические уравнения, решаемые путем понижения степени уравнения
Слайд 105
Решение однородных тригонометрических уравнений
Определение: Тригонометрическое уравнение называется однородным,
если показатели степени слагаемых равны.
Слайд 106
Ну, а теперь – графики! На первый взгляд
сложные и непонятные графики тригонометрических функций.
Знакомьтесь! График функции
синус!
Слайд 107
х
у
0
0
2π
1
-1
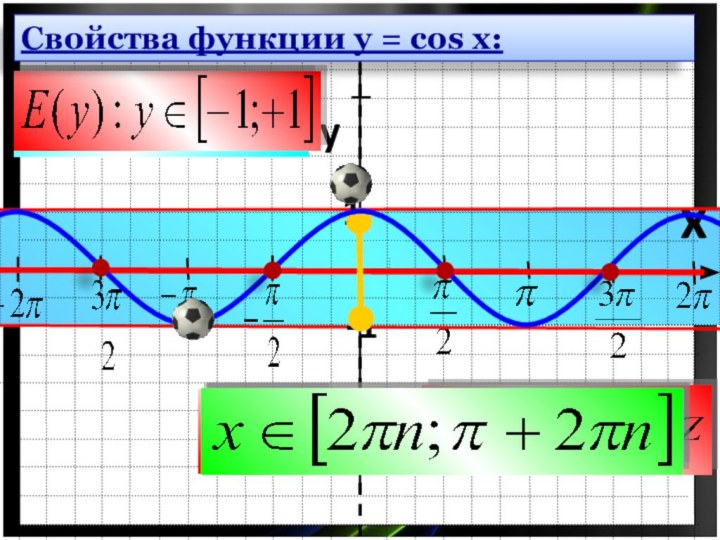
D(у) = (- ∞ ; + ∞ )
Е(у)=
[-1; 1]
Область определения.
Область значений функции.
Область определения
функции
синус ̶ любое
действительное число, т. е.
2) Область значений функции синус ̶ отрезок
от -1 до 1, т. е.
х, т. е.
f (− х)= − f (х)
функция нечетная
f (х +Т) = f (х –Т) = f (х) Функция периодическая,
T = 2π – наименьший положительный период
Периодичность
sin (x +2n) = sin х, n ϵ Z
Чётность, нечётность
x
y
0
0
M
y
2
-y
x
-x
Слайд 109
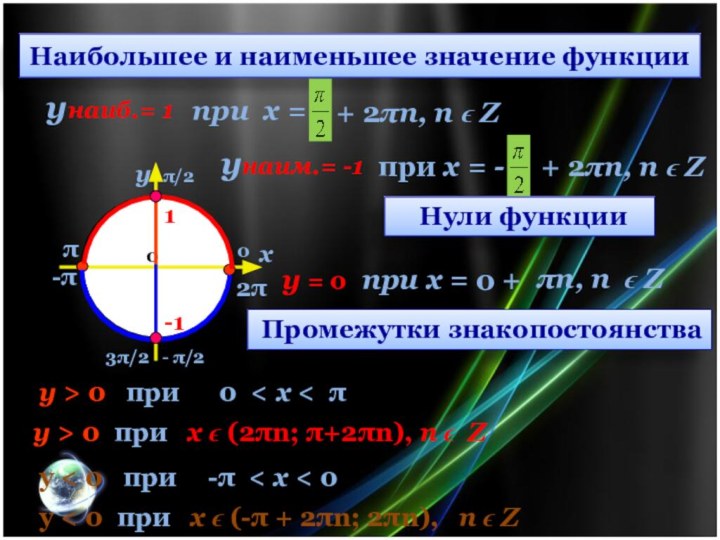
Наибольшее и наименьшее значение функции
y > 0
при 0 < x < π
y > 0 при х ϵ (2πn; π+2πn), n ϵ Z
y < 0 при -π < x < 0
y < 0 при х ϵ (-π + 2πn; 2πn), n ϵ Z
у
- π/2
3π/2
2π
х
0
-π
0
π
π/2
при х =
при х = -
1
-1
унаиб.= 1
+ 2n, n ϵ Z
унаим.= -1
+ 2n, n ϵ Z
у = 0
πn, n ϵ Z
0
+
Промежутки знакопостоянства
Нули функции
Слайд 110
Промежутки монотонности
у
2
π
х
0
0
π
-π
-
2
π
π
2
3
у 1
у 2
М 1
М 2
Функция возрастает на
- /2 + 2n; /2 + 2n
, n
Функция убывает на /2 + 2n; 3/2 + 2n , n Z
Z
х1
х2
I. х 1 х 2
IV х 1 х 2
sin х 1 sin х 2
II. х 1 х 2
sin х1 sin х 2
III. х 1 х 2
sin х 1 sin х 2
sin х 1 sin х2
Слайд 111
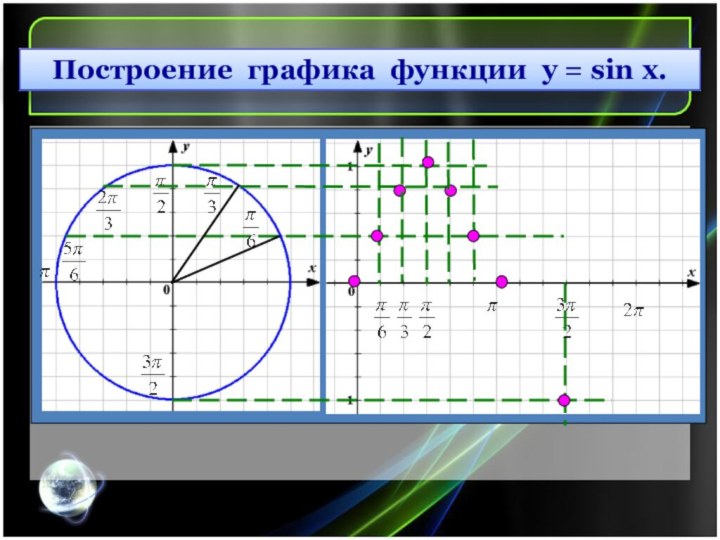
Построение графика функции y = sin x.
Слайд 112
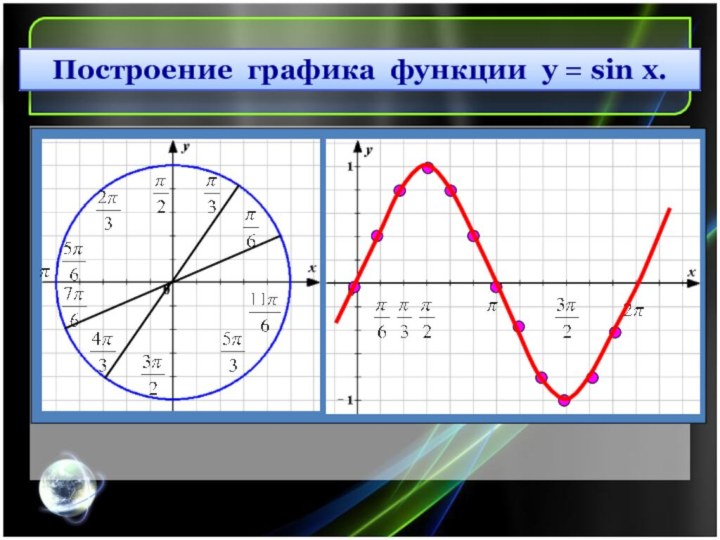
Построение графика функции y = sin x.
Слайд 113
Построение графика функции y = sin x.
I
I I I I
O
x
y
-1
1
1/2
Найти все корни уравнения sin x = 1/2
принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
y = sin x.
Ответ: х = π/6; х = 5π/6
Пример №1
I
I I I I
O
x
y
-1
1
1/2
Найти все решения неравенства sin x ≥ 1/2
принадлежащих промежутку –3π/2 ≤ х ≤ π .
y = sin x.
Ответ:
Пример №2
Слайд 116
y
x
1
-1
cos
=
x
y
Построение графика функции:
Слайд 119
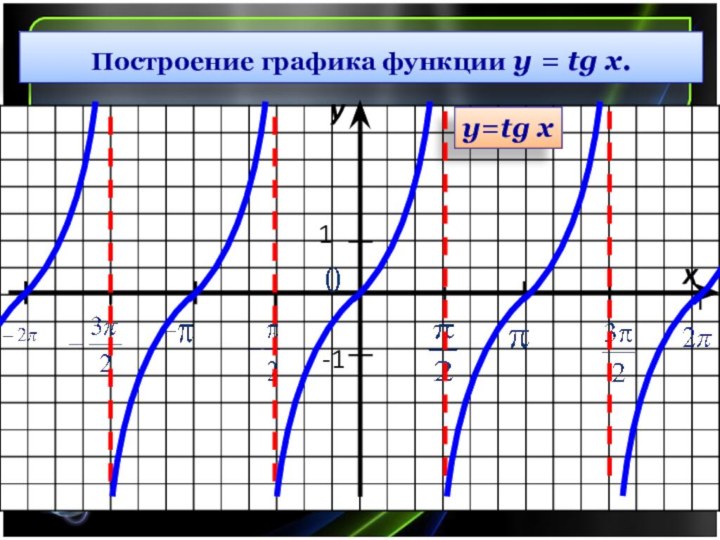
Построение графика функции y = tg x.
y
x
1
-1
у=tg
Слайд 120
y
x
1
-1
у=tg x
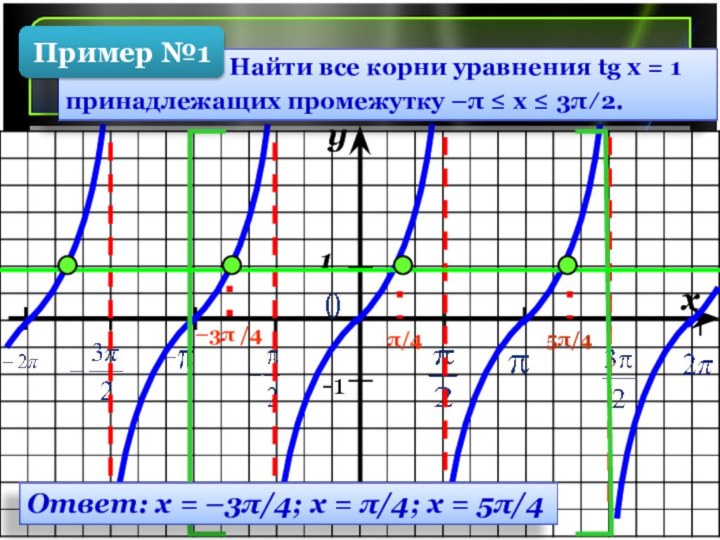
Построение графика функции y = tg x.
Найти все корни
уравнения tg x = 1
принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
–3π /4
π/4
5π/4
Ответ: х = –3π/4; х = π/4; х = 5π/4
Пример №1
Слайд 122
y
x
1
-1
–3π /4
π/4
5π/4
Ответ:
Найти все
решения неравенства tg x ≥ 1
принадлежащих промежутку –3π/2 ≤ х ≤ π .
Пример №2
Слайд 124
Ох, уж эта тригонометрия! Опять ЕГЭ! Решаем задания
из ЕГЭ!
! !
!
По мнению многих учеников, запись «n €
Z» - избыточная. А как думаете, Вы?
Тригонометрия
на ЕГЭ Задания В5
Решите уравнение .
В ответе напишите наибольший отрицательный корень.
Задания В7
Найдите значение выражения .
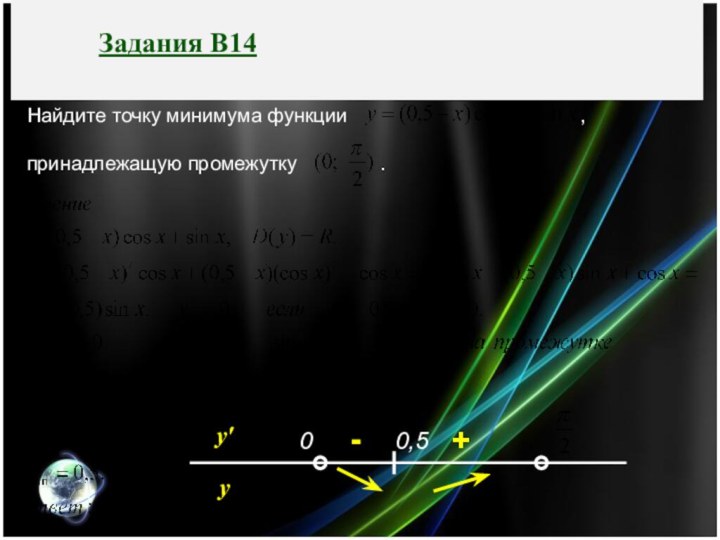
Задания В14
Найдите точку минимума функции ,
принадлежащую промежутку .
у'
у
0,5
0
-
+
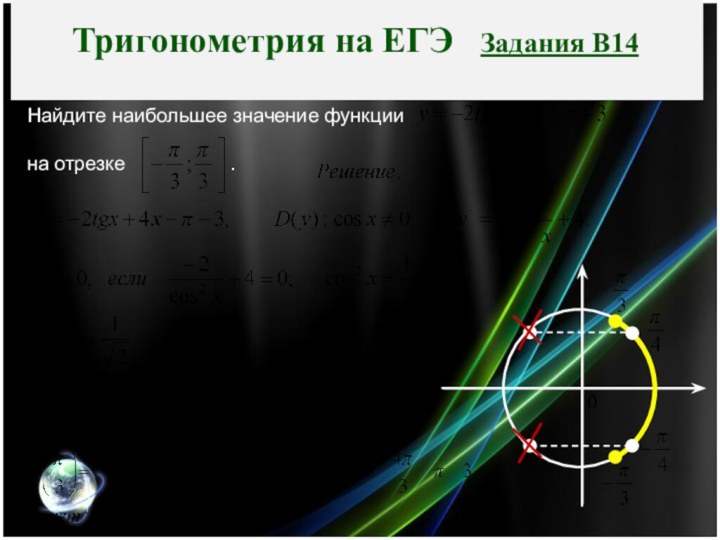
Тригонометрия
на ЕГЭ Задания В14
Найдите наибольшее значение функции
на отрезке .




















































![Презентация Электронное пособие по тригонометрии arcsin ааarcsin (-a)= –arcsin a-а-arcsin аАрксинусом числа а [-1;1 ] называют](/img/tmb/7/666698/074c8b722aa5b201d495f32e8735f6b9-720x.jpg)















![Презентация Электронное пособие по тригонометрии ху002π1-1D(у) = (- ∞ ; + ∞ )Е(у)= [-1; 1] Область определения.](/img/tmb/7/666698/9da3266b4b9fae7f241874bfeb122ace-720x.jpg)