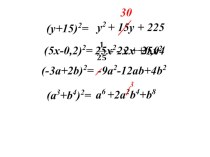- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параметры в тригонометрии 10-11 класс
Содержание
- 2. Подходы решений тригонометрических уравнений с параметрами Рассмотрим
- 3. Введение дополнительных переменныхНайдите все значения параметра a,
- 4. Вспомогательные преобразованияНайти а при котором имеет по крайней мере одно решение уравнение
- 5. Решение: Преобразуем это уравнение, используя формулы сокращенного умножения и основное тригонометрическое тождество:
- 6. Разделим обе части уравнения на 4:
- 7. В левой части уравнения вынесем за скобки
- 8. Зная, что следовательно значит Ответ: при
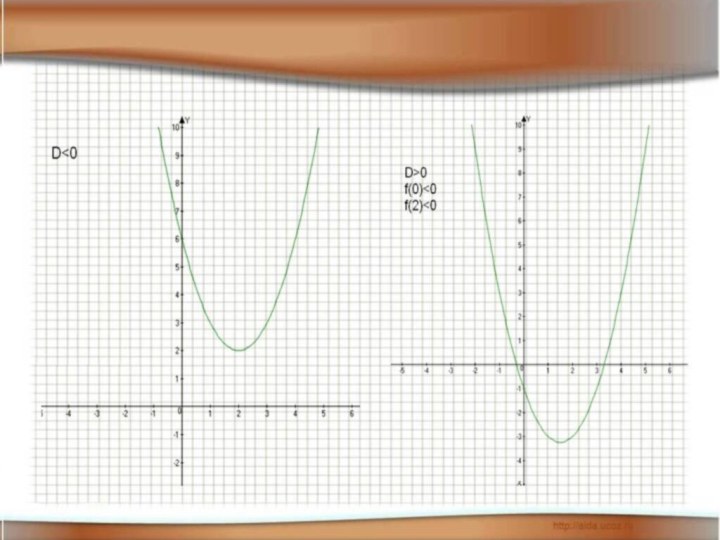
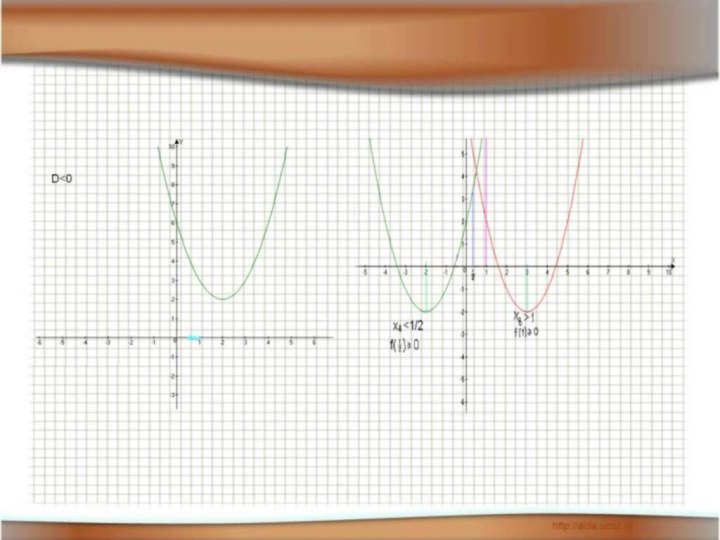
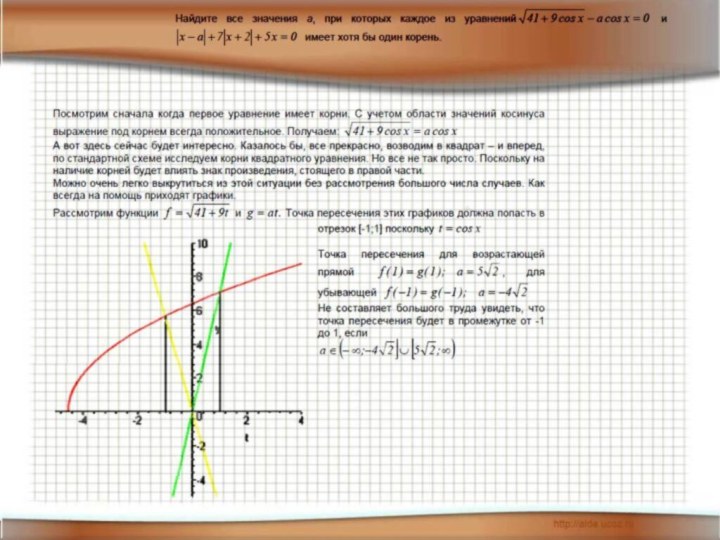
- 9. Графический метод.
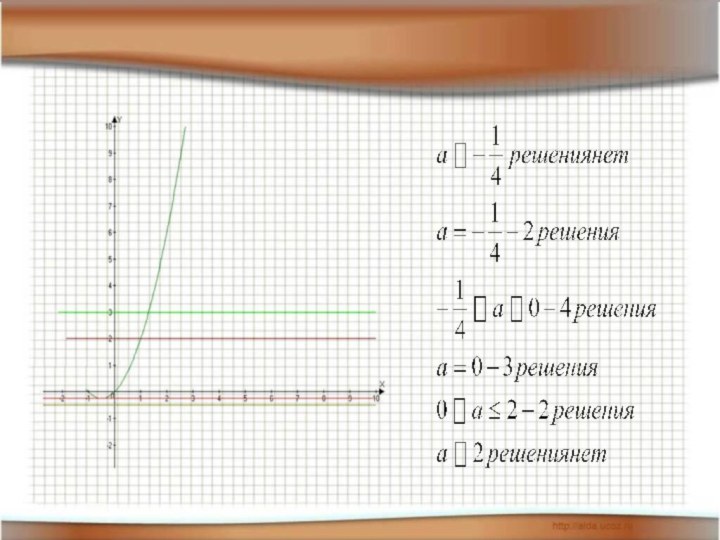
- 12. Найти все значения параметра а, при которых уравнение имеет ровно 2 корня.
- 13. При всех значениях параметра а решите уравнение
- 18. Выясните, при каких значениях параметра а неравенствовыполняется на отрезке
- 20. Выясните, сколько корней в зависимости от а на имеет уравнение
- 27. Применение классических формулНайти наибольшее значение функциигде
- 28. Решение: Найдем наибольшее значение квадрата этой функцииС учетом того, что имеем
- 29. Выражение примет наибольшее значение тогда, когда наибольшее значение будет иметь подкоренное выражение. Имеем
- 30. Если сумма двух положительных переменных постоянна, то
- 31. В этом случае каждое из подкоренных выражений
- 32. Скачать презентацию
- 33. Похожие презентации
Подходы решений тригонометрических уравнений с параметрами Рассмотрим некоторые общие подходы при решении определенных типов тригонометрических уравнений с параметрами. В дальнейшем будем обозначать вектор параметров уравнения через a.




























Слайд 3
Введение дополнительных переменных
Найдите все значения параметра a, при
котором неравенство справедливо при всех значениях X.
|3sin2x
+ 2a sinx cosx + cos2x + a| <= 3
Слайд 4
Вспомогательные преобразования
Найти а при котором имеет по крайней
мере одно решение уравнение
Слайд 5 Решение: Преобразуем это уравнение, используя формулы сокращенного умножения
и основное тригонометрическое тождество:
Слайд 7
В левой части уравнения вынесем за скобки
и
получим:
значит решений нет
При
При
получаем
При
получаем
При
получаем
При
При
При
Зная, что
следовательно
значит
Слайд 29 Выражение примет наибольшее значение тогда, когда наибольшее значение
будет иметь подкоренное выражение. Имеем
Слайд 30 Если сумма двух положительных переменных постоянна, то произведение
этих переменных имеет наибольшее значение, когда оба сомножителя принимают
одинаковые значения.Если
то
Слайд 31 В этом случае каждое из подкоренных выражений равно
(1+a)/2 и
Если , то значение функции будет
2.Ответ: