Слайд 2
Решая задачи по теории вероятностей, мы постоянно используем
одну и ту же формулу, которая одновременно является классическим
определением вероятности:
где k — число благоприятных исходов, n — общее число исходов.
Теория вероятностей
Слайд 3
Напомним, что ответом к задачам с кратким ответом
могут быть только целые числа или конечные десятичные дроби,
поэтому полученную обыкновенную дробь необходимо переводить в десятичную.
Во избежание ошибок следует различать два типа условий. В условиях вида «из 100 сумок 8 дефектных» имеется в виду, что всего сумок 100, из них дефектных — 8, качественных — 92. В условиях вида «на каждые 100 сумок приходится 8 дефектных» предполагается, что всего сумок 108, из них дефектных — 8, качественных — 100.
Приведем пример такого задания.
Задание. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной.
Результат округлите до сотых.
Решение. По условию из 108 сумок 100 являются качественными. Поэтому искомая вероятность равна
Ответ: 0,93.
Слайд 4
Задача .Изготовили 100 деталей,
из которых 97 стандартных и
3 бракованных.
Какова вероятность выбора стандартной детали и выбора
бракованной детали?
Ответ: 0,97 ; 0,03
Задача .Бросают игральную кость.
Найти вероятность того, что: а) выпадет четное число очков (А); б) выпадет число очков, кратное 3 (В); в) выпадет любое число очков, кроме 5 (С).
Слайд 5
Задача .Известно, что 5%
всех мужчин и 0,25%
всех женщин – дальтоники. Наудачу выбранное лицо страдает дальтонизмом.
Какова вероятность того, что это лицо – мужчина (считать, что мужчин и женщин одинаковое число).
Слайд 7
На семинар приехали 3 ученых из Норвегии, 3
из России и 4 из Испании. Порядок докладов определяется
жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Заметим, что поскольку порядок докладов определяется жеребьевкой, вероятность того, что восьмым окажется доклад ученого из России такая же, как вероятность того, что доклад ученого из России окажется первым. То есть эта вероятность не зависит от номера выступления.
Слайд 8
Научная конференция проводится в 5 дней. Всего запланировано
75 докладов — первые три дня по 17 докладов,
остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Слайд 9
Вася выбирает трехзначное число. Найти вероятность того, что
оно делится на 6. Ответ округлите до сотых.
Слайд 11
Перед началом первого тура чемпионата по бадминтону участников
разбивают на игровые пары случайным образом с помощью жребия.
Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Слайд 12
В случайном эксперименте симметричную монету бросают четырежды. Найдите
вероятность того, что орел не выпадет ни разу.
Слайд 13
Задача .Если абонент ждет телефонного вызова с 2
до 3 часов, то какова вероятность того, что этот
вызов пройдет с 2ч 30мин до 2ч 40мин.?
Задача .На листок бумаги в клетку
со стороной 10 мм падает кружок
диаметра 2 мм. Какова вероятность того, что кружок целиком попадет внутрь клетки?
Слайд 14
Задача .Внутри прямоугольного параллелепипеда, измерения которого равны 4,
6, 10см, наудачу выбирается точка М.
Какова вероятность того,
что она окажется внутри данного куба, ребро которого 3см?
Слайд 15
Вероятность того, что электронная книга прослужит больше трёх
лет, равна 0,86. Вероятность того, что она прослужит больше
пяти лет, равна 0,72. Найдите вероятность того, что она прослужит меньше пяти лет, но больше трёх.
Р = 0,86(5 лет)-0,72(3 года)=0,14(больше 3, но меньше 5)
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
Р = 0,82-0,51=0,31 (число пассажиров от 10 до 17)
Слайд 16
Задача .Набирая номер телефона,
абонент забыл одну цифру
и набрал ее наудачу.
Найти вероятность того,
что набрана
нужная цифра.
Слайд 17
Задача .Набирая номер телефона,
абонент забыл две цифры
и набрал их наудачу.
Определить вероятность того,
что найдены
нужные цифры.
Слайд 18
Задача .Набирая номер телефона, абонент забыл две цифры
и набрал их наудачу. Определить вероятность того,
что найдены
нужные цифры.
Слайд 19
Задача .Даны 5 точек, никакие
3 из которых
не лежат на одной прямой. Найти вероятность того, что,
выбрав наугад 2 точки, ученик получит нужную прямую.
Формула прекрасно работает до тех пор, пока задачи были легкими, а числа, стоящие в числителе и знаменателе — очевидными.
Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений n и k становится проблематичным. В таком случае на помощь приходит комбинаторика.
Слайд 23
Задача .Даны 5 точек, никакие 3 из которых
не лежат на одной прямой. Найти вероятность того, что,
выбрав наугад 2 точки, ученик получит нужную прямую.
Слайд 24
Задача .Декан факультета вызвал
через старосту трех студентов
из группы, состоящую из 5 не выполнивших задания человек.
Староста забыл фамилии
вызванных студентов и послал наудачу трех студентов
из указанной группы. Какова вероятность того, что к декану явятся именно вызванные
им студенты?
Слайд 26
В случайном эксперименте симметричную монету бросают четырежды. Найдите
вероятность того, что орел не выпадет ни разу.
Можно эту
задачу решить и таким способом:
Пусть монету бросают n раз. Тогда вероятность того, что орел (решка) выпадет ровно k раз, можно найти по формуле:
Слайд 27
Задача .Буквы а, а, в, к, к, о,
х написаны на отдельных карточках.
Какова вероятность того,
что извлекая
все эти карточки
по одной наудачу
(без возвращения обратно), получим в порядке их выхода слово Каховка?
Слайд 29
Задача .В ящик, имеющий два отделения, брошено два
шарика.
Какова вероятность того,
что в каждом отделении будет
находиться один шарик?
Слайд 30
Задача .В библиотечке 25 книг.
Наудачу выбирается 3
книги.
Какова вероятность того,
что будут выбраны
нужные книги?
Слайд 31
Задача .Проверено 100 деталей.
Среди них оказалось 80
стандартных. Какова относительная частота появления стандартной детали?
Слайд 32
Во время вероятностного эксперимента монету бросили 1000 раз,
532 раза выпал орел. На сколько частота выпадения решки
в этом эксперименте отличается от вероятности этого события?
Частота события x -- отношение N(x) / N числа N(x) наступлений этого события в N испытаниях к числу испытаний N.
Если орел выпал 532 раза, то решка выпала 1000-532=468
Частота этого события равна
Вероятность выпадения решки равна 0,5. Следовательно, частота выпадения решки в этом эксперименте отличается от вероятности этого события на |0,5-0,468|=0,032
Ответ: 0,032
Слайд 33
Задача .Естествоиспытатель К.Пирсон подбрасывал монету и записывал полученный
результат. Проделав эту операцию 24000 раз, обнаружил, что герб
выпадал в 12012 случаях.
Какова относительная частота выпадения герба?
Слайд 34
Задача .Отдел технического контроля обнаружил
5 бракованных книг
в партии из случайно
отобранных 100 книг. Найти относительную
частоту появления бракованных книг.
Ответ: 0,05.
Задача .При испытании партии приборов относительная частота
годных приборов 0,9. Найти число годных приборов, если всего было проверено 200 приборов.
Ответ: 180.
Слайд 35
Задача .Два друга Х и У условились встретиться
в определенном месте между
12 и 13 часами, при
этом пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи друзей Х и У, если приход каждого из них в течение указанного часа может произойти
наудачу и моменты прихода
независимы?
Х
У
Слайд 36
Пусть момент прихода друзей Х и У соответственно
x и y.
Для того, чтобы встреча произошла, необходимо и
достаточно выполнения неравенства |х-у| ≤ 20, или -20 ≤ х-у ≤ 20.
В прямоугольной системе координат множество точек (х;у),
координаты которых удовлетворяют неравенству, образуют полосу (рис.в):
у
у
у
у
х
х
х
х
20
-20
20
-20
20
20
-20
-20
0
60
60
х-у ≤20
-20≤ х-у
а)
б)
в)
г)
-20≤ х-у≤ 20
Слайд 37
Задача .В урне 5 белых шаров,
3 черных,
2 в полоску и 7 в клетку.
Найти вероятность
того, что из урны будет извлечен одноцветный шар.
Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P (A) + P (B).
Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании. В противном случае события называются совместными.
Слайд 38
Задача .Имеется 100 лотерейных билетов.
Известно, что на
5 билетов попадает выигрыш
по 20 руб., на 10
– по 15 руб., на 15 – по 10 руб.,
на 25 – по 2 руб. и на остальные – ничего.
Найти вероятность того, что на купленный билет будет получен выигрыш не меньше 10 руб.
Слайд 39
Задача .В коробке 250 лампочек, из них
100
по 100 Вт, 50 – по 60 Вт, 50
- по 25 Вт,
50 - по 15 Вт. Вычислить вероятность того, что мощность любой взятой наугад лампочки
не превысит 60 Вт.
Слайд 40
Задача .В коробке лежат 30 галстуков, причем 12
из них красные, остальные белые.
Определить вероятность того, что
из 4 наудачу вынутых галстуков все они окажутся одного цвета.
Слайд 41
Задача .Вероятность того, что студент сдаст экзамен на
отлично, равна 0,2; на хорошо – 0,4; на удовлетворительно
– 0,3;
на неудовлетворительно – 0,1. Определить вероятность того,
что студент сдаст экзамен.
1 способ.
Р(А+В+С) = Р(А)+Р(В)+Р(С) = 0,2+0,4+0,3 = 0,9
2 способ.
Сумма вероятностей событий, образующих полную систему, равна 1, тогда
Р(А+В+С) = 1 – Р(D) = 1 - 0,1 = 0,9
Ответ: 0,9.
Слайд 42
Задача .В ящике 10 лампочек по15 Вт,
10
– по 25 Вт, 15 – по 60 Вт
и 25 – по 100 Вт.
Определить вероятность того, что взятая наугад лампочка имеет мощность более 60 Вт,
если известно, что число ватт на взятой лампочке – четное.
Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей: P (AB) = P (A) P (B).
Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.
Слайд 43
Задача .В ящике 10 лампочек по15 Вт,
10
– по 25 Вт, 15 – по 60 Вт
и 25 – по 100 Вт.
Определить вероятность того, что взятая наугад лампочка имеет мощность более 60 Вт,
если известно, что число ватт на взятой лампочке – четное.
Слайд 44
Задача .В первой урне находятся
6 черных и 4
белых шара,
во второй – 5 черных и 7
белых.
Из каждой урны извлекают
по одному шару. Какова вероятность того, что оба шара окажутся белыми?
Слайд 45
Найдите вероятность того, что пятизначный цифровой код доступа
не содержит нулей
Слайд 46
Задача. Прибор состоит из двух элементов, работающих независимо.
Вероятность
выхода из строя
первого элемента равна 0,2;
Вероятность выхода из
строя
второго элемента равна 0,3.
Найти вероятность того, что:
а) оба элемента выйдут из строя;
б) оба элемента будут работать.
Пусть событие А – выход из строя первого элемента, событие Е – выход
из строя второго элемента. Эти события независимы ( по условию).
а) одновременно появление А и Е есть событие АЕ Р(АЕ) = 0,2·0,3 = 0,06
б) если работает первый элемент, то имеет место событие Ā (противоположное событию А – выходу этого элемента из строя);
Если работает второй элемент – событие Ē, противоположное событию Е
Р(Ā) =1- 0,2 = 0,8 и Р(Ē) = 1-0,3 = 0,7
Тогда событие, состоящее в том, что будут работать оба элемента,
есть ĀĒ. Р(ĀĒ) = Р(Ā)·Р(Ē) = 0,8·0,7 = 0,56.
Событие A, состоящее в том, что событие A не происходит, называют противоположным к событию A.
Слайд 47
Задача .В экзаменационные билеты включено по 2 теоретических
вопроса
и по 1 задаче.
Всего составлено 28 билетов.
Вычислить
вероятность того,
что, вынув наудачу билет,
студент ответит на все вопросы,
если он подготовил 50 теоретических вопросов
и 22 задачи.
Слайд 49
Задача .В Санкт-Петербург – 15 мест на практику,
в Киев – 10, в Баку – 5. Какова
вероятность того, что определенные три студента попадут в один город?
Слайд 50
Задача .Какова вероятность того,
что при 10 бросаниях
игрального кубика «четверка» выпадет: а) ровно 3 раза;
б)
ровно 2 раза; в) ровно 6 раз;
г) не выпадет ни разу?
Пусть проведена серия независимых испытаний, в каждом из которых вероятность появления события A равна p (схема Бернулли). Тогда вероятность того, что в серии из n испытаний событие A появится ровно k раз, выражается формулой Бернулли
Слайд 52
Задача .Найти вероятность того, что при 9 бросаниях
монеты «орел» выпадет ровно 4 раза.
Или еще способ решения
этой задачи:
Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Слайд 53
Задача .За один выстрел стрелок поражает мишень с
вероятностью 0,1.
Найти вероятность того,
что при 5 выстрелах он
хотя бы раз попадет
в мишень.
Слайд 54
Задача .В следующих испытаниях найдите вероятности «успеха» и
«неудачи»:
а) Бросают пару различных монет. «Неудача» – выпадение двух
орлов.
б) Бросают игральный кубик.
«Успех» – выпадение числа, кратного трем.
в) Бросают пару различных кубиков.
«Неудача» – выпадение двух
четных чисел.
г) Из 36 игральных карт берут 5.
«Успех» – среди них нет дамы пик.
Ответы:
а) 0,75 , 0,25
б) 1 , 2
3 3
в) 0,75 , 0,25
г) 31 , 5
36 36
Слайд 55
Задача .Напишите формулы,
по которым следует находить вероятность
того, что при 4 бросаниях игрального кубика «тройка» выпадет:
а)
ровно 2 раза
б) ровно 3 раза
в) ровно 4 раза
г) не выпадет ни разу
д) вычислите вероятности
этих событий
Слайд 56
Задача .Из набора домино случайно вытаскивают одну «доминошку»,
записывают сумму очков на ней, и возвращают ее обратно.
Так
делают 3 раза.
Найдите вероятность того, что:
а) дубль появляется ровно 1 раз;
б) дубль появляется ровно 2 раза;
в) дубль появляется хотя бы раз;
г) сумма очков на «доминошке» каждый раз больше 9.
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Слайд 58
Правило произведения. Пусть требуется выполнить последовательно k действий.
Если первое действие можно выполнить n1 способами, второе действие
n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Слайд 59
Задача . В первый ящик положили
5 мобильников,
а во второй – 3 мобильника. Сколькими способами можно
вытащить один мобильник?
Из 1 ящика можно вытащить пятью способами, а из 2 – тремя способами. Всего существует 5+3 = 8 способов.
Задача . В первом ящике 5 мобильников с зеленым корпусом, а во втором – 3 мобильника с красным корпусом.
Сколькими способами можно вытащить один зеленый и один красный мобильник?
Зеленые мобильники можно выбрать пятью способами, красные – тремя способами. Всего 1 зеленый и 1 красный можно выбрать
3 · 5 = 15 способами.
Слайд 60
Задача . Сколько не более чем трехзначных чисел
можно составить из цифр 1,2,3,4,5 так, чтобы цифры в
числах
не повторялись?
Надо узнать, сколько можно составить
однозначных, двузначных или трехзначных чисел.
По правилу суммы их будет N = N1+N2+N3.
Однозначных чисел будет 5, значит, N1 = 5.
На месте десятков двузначных чисел можно поставить
любую из пяти цифр. После каждого такого выбора на месте единиц можно поставить любую из четырех оставшихся цифр, т.к. цифры в числе не должны повторяться. По правилу произведения N2 = 5·4 = 20.
Рассуждая аналогично, получим число различных трехзначных чисел N3 = 5· 4· 3 = 60.
Следовательно, N = 5+20+60 = 85.
Слайд 61
Задача .В одной вазе лежит
5 яблок, а в
другой -8 мандаринов.
Сколькими способами можно выбрать:
а) яблоко или
мандарин;
б) яблоко и мандарин?
Ответы:
а) N = 5+8 = 13
б) N = 5· 8 = 40
Задача .Ученик должен выполнить
практическую работу по математике.
Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии.
Сколькими способами он может выбрать одну тему для практической работы?
N = 17+13 = 30
Ответ: 30.
Слайд 62
Задача .В танцевальном кружке
5 мальчиков и
4 девочки.
Руководитель хочет отобрать пару, состоящую из 1
мальчика и 1 девочки для участия в соревнованиях.
Сколько он должен посмотреть пар, чтобы выбрать лучшую пару?
N = 5·4 = 20
Ответ: 20.
Слайд 63
Задача . Имеется 5 билетов
денежно-вещевой лотереи,
6 билетов
спортлото
и 10 билетов автомотолотереи.
Сколькими способами можно выбрать 1
билет из спортлото
или автомотолотереи?
Денежно-вещевая лотерея в выборе не участвует, поэтому 10+6=16
Задача .Сколько имеется путей,
которыми можно попасть
из города А в город С через город В, если из А в В ведут две дороги,
а из В и С – три дороги?
N = 2·3 = 6
Ответ: 6.
Слайд 64
Задача .На книжной полке стоят
25 книг по
математике,
15 – по физике,
10 – по астрономии.
Сколькими способами
можно
выбрать 3 книги так, чтобы одна книга была по математике,
другая – по физике и третья – по астрономии?
N = 25· 15· 10 = 3750
Ответ: 3750.
Слайд 65
Задача .Сколько четных двузначных чисел можно составить из
цифр 0,1,2,4,5,9?
Составим таблицу: слева от первого столбца – первые
цифры искомых чисел, а выше первой строки – вторые цифры этих чисел (учитывая, что числа – четные, т.е. оканчиваются на 0,2,4).
5 строк · 3 столбика = 15 чисел
Ответ: 15.
Слайд 66
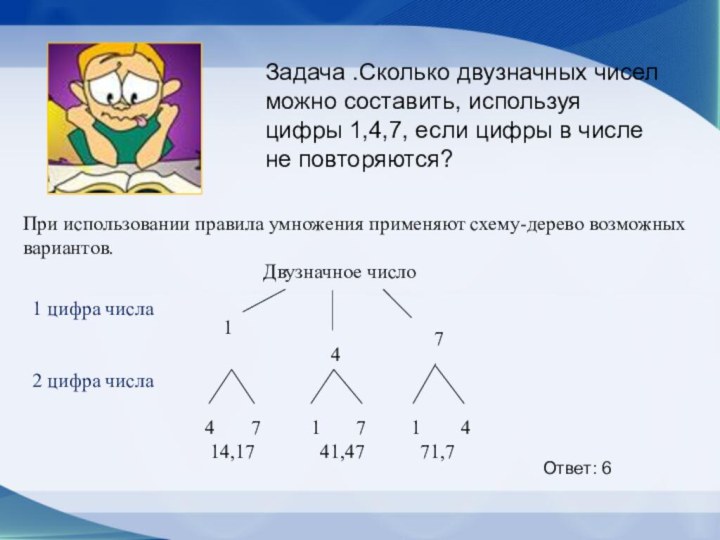
Задача .Сколько двузначных чисел можно составить, используя цифры
1,4,7, если цифры в числе не повторяются?
Ответ: 6
Слайд 67
Задача .На завтрак Вова может выбрать плюшку, бутерброд,
пряник или кекс,
а запить их он может кофе,
соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Составим таблицу.
3 строки · 4 столбика = 12 вариантов завтрака
Ответ: 12.
Слайд 68
Задача. Сколько двузначных чисел
можно записать в десятичной
системе
счисления?
9 строк ·10 столбиков = 90 чисел
М
С К
2 овощ С К М К М С
Варианты МС, МК, СМ, СК, КМ, КС
6 вариантов, но блюда МС и СМ, МК и КМ, КС и СК совпадают, поэтому 3 пары блюд Ответ: 3.
Задача. Служитель зоопарка должен дать зайцу 2 различных овоща.
Сколькими способами он может
это сделать, если у него есть морковь, свекла и капуста?
Завтрак зайца
Слайд 70
Задача. Туристическая фирма планирует посещение туристами
в
Италии трех городов:
Венеции, Рима и Флоренции.
Сколько существует вариантов
такого маршрута?
Варианты ВРФ, ВФР, РВФ, РФВ ФВР, ФРВ
Ответ: 6.
Слайд 71
Задача. Несколько стран в качестве символа своего государства
решили использовать флаг в виде трех горизонтальных полос одинаковых
по ширине,
но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой,
отличный от других, флаг?
Ответ: 6.
Слайд 72
1 способ. По правилу умножения: N = 2·
2· 2 = 8
2 способ. + горит,
- не горит
+++
++-
+-+
+--
-++
---
-+-
--+
Ответ: 8.
Задача. В коридоре висят
три лампочки.
Сколько различных способов
освещения коридора?
Слайд 73
Задача .Сколько различных пятизначных чисел можно составить из
цифр 1,2,3,4,5 при условии, что ни одна цифра в
числе не повторяется?
Р5 = 5! = 1· 2· 3· 4 ·5 = 120
Задача. В соревнованиях участвовало 4 команды.
Сколько вариантов распределения мест между ними возможно?
Р4 = 4! = 1· 2· 3· 4 = 24
Задача .Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?
Р8= 8!=1· 2· 3· 4· 5· 6· 7· 8 = 40320
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Слайд 74
Задача .Сколькими способами
можно разместить 12 человек
за
столом, возле которого поставлены 12 стульев?
Р12 = 12! =
479001600
Задача .Сколькими способами
7 книг разных авторов
можно расставить на полке
в один ряд?
Р7 = 7! = 5040
Слайд 75
Задача .Сколько двузначных чисел можно составить из пяти
цифр 1,2,3,4,5 при условии, что ни одна
из них
не повторяется?
Задача .У нас есть 9 книг из серии «Занимательная математика». Сколькими способами можно подарить 3 из них?
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Слайд 76
Задача .Сколько существует вариантов распределения трех призовых мест,
если в розыгрыше участвуют 7 команд?
Задача .Сколько вариантов расписания
можно составить на один день, если всего имеется
8 учебных предметов, а в расписании на день могут быть включены
только три из них?
Слайд 77
Задача .Сколько вариантов распределения
трех путевок в санатории
различного профиля
можно составить
для пяти претендентов?
Задача .В городе проводится
первенство по футболу.
Сколько в нем состоится матчей,
если участвуют
12 команд?
Слайд 78
Задача .Сколько сигналов можно подать 5 различными флажками,
поднимая
их в любом количестве
и в произвольном порядке?
Слайд 79
Задача .Сколько трехзначных чисел можно составить из цифр
1,2,3,4,5?
Классической задачей комбинаторики является задача о числе размещений с
повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Слайд 81
Задача .В тренировках участвовали
12 баскетболистов. Сколько различных
стартовых пятерок
может образовать тренер?
Задача .Сколькими способами
можно заполнить
лотерейный билет «5 из 36»?
Задача .Сколькими способами читатель может выбрать
2 книжки из 6 имеющихся?
Слайд 82
Задача .Сколькими способами можно составить дозор из трех
солдат и одного офицера, если имеется 80 солдат и
3 офицера?
Задача .Сколькими способами можно выбрать двух человек в президиум, если на собрании присутствует 78 человек?
Слайд 83
Задача .Номер автомашины состоит из трех букв русского
алфавита и трех цифр. Сколько различных номеров
автомашин можно
составить?
Слайд 84
Задача . В кондитерском магазине продают 4 сорта
пирожных: эклеры, песочные, бисквитные и слоеные. Сколькими способами можно
купить 7 пирожных?
Слайд 85
Задача .В книжный магазин поступили
романы Ф.Купера «Прерия», Зверобой»,
«Шпион», «Пионеры», «Следопыт»
по одинаковой цене. Сколькими способами библиотека
может закупить 17 книг на выбранный чек?
Слайд 86
Задача . Сколькими способами можно переставить буквы слова
«ананас»?
Для случая, когда среди выбираемых n элементов есть одинаковые
(выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Задача .Сколько перестановок
можно сделать из букв
слова «Миссисипи»?