Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Высшая математика. Линейная алгебра

Содержание

2. СодержаниеЭлементы линейной алгебрыЗадачи линейного программированияГрафический метод решения ЗЛПСимплексный метод решения ЗЛПДвойственные задачиТранспортная задачаАнализ временных рядов
3. Элементы линейной алгебрыЛекция 1
4. Определители Определение. Определителем 2-го порядка
5. Определителем 3-го порядка называется выражение
6. Правило треугольника Способ вычисления определителей 3-го порядка
7. Пример Найдем определитель
8. Ранг матрицы. Рассмотрим матрицу А
9. Определение. Наивысший порядок отличного от
10. Можно показать, что элементарные преобразования
11. Пример С помощью элементарных преобразований вычислить ранг матрицы
12. Система m линейных уравнений с n неизвестными
13. Для того чтобы система линейных
14. Метод Гаусса решения систем линейных уравнений
15. Назовем матрицей системы матрицу, составленную
16. Элементарные преобразования Для того чтобы решить
17. Разрешается: 1) изменять порядок
18. Пример Решить систему
19. Общее решение системы линейных уравнений
20. Пример Решить систему Расширенная матрица этой системы
21. Переменные
22. Метод Жордана –Гаусса решения СЛАУ Решаем систему уравнений
23. В процессе решения могут встретиться
24. 2)на некотором этапе получилась матрица ,
25. Придавая каждой из
26. Пример. Решить методом Жордана-Гаусса систему Расширенная матрица системы
27. 1-я итерация. За направляющий элемент берем
28. Вторая итерация. Выбираем направляющий элемент
29. Третья итерация. Берем за направляющий элемент
30. Исходная система равносильна следующей:
31. Метод Жордана –Гаусса в excel. Открыть
32. Функции МУМНОЖ—умножение матриц ТРАНСП—транспонирование
34. Вычислить определитель#число!
36. Решить в excel систему
37. Решить в excel систему Мы
39. Следующее действие Нажимаем одну за другой
42. Скачать презентацию
43. Похожие презентации

СодержаниеЭлементы линейной алгебрыЗадачи линейного программированияГрафический метод решения ЗЛПСимплексный метод решения ЗЛПДвойственные задачиТранспортная задачаАнализ временных рядов

Главная
Алгебра
Высшая математика. Линейная алгебра

Высшая математикаКафедра математики и моделированияПреподаватель Никулина Л. С.Четвертый семестр.

СодержаниеЭлементы линейной алгебрыЗадачи линейного программированияГрафический метод решения ЗЛПСимплексный метод решения ЗЛПДвойственные задачиТранспортная задачаАнализ временных рядов

Определители Определение. Определителем 2-го порядка называется выражение

Определителем 3-го порядка называется выражение

Правило треугольника Способ вычисления определителей 3-го порядка называется правилом треугольника. Элементы, входящие

Ранг матрицы. Рассмотрим матрицу А размера

Определение. Наивысший порядок отличного от нуля минора матрицы называется ее

Можно показать, что элементарные преобразования не меняют ранга матрицы.

Пример С помощью элементарных преобразований вычислить ранг матрицы

Система m линейных уравнений с n неизвестными Рассмотрим систему m линейных

Для того чтобы система линейных уравнений была совместной, необходимо и

Метод Гаусса решения систем линейных уравнений Для того чтобы решить систему

Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу,

Элементарные преобразования Для того чтобы решить систему уравнений выписывают расширенную матрицу

Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению

Общее решение системы линейных уравнений Определение. Если ранг матрицы равен

Пример Решить систему Расширенная матрица этой системы имеет вид Минор 3-го

Метод Жордана –Гаусса решения СЛАУ Решаем систему уравнений

В процессе решения могут встретиться следующие случаи : 1) в

2)на некотором этапе получилась матрица , содержащая единичных столбцов.

Придавая каждой из стоящих в правых частях равенств

Пример. Решить методом Жордана-Гаусса систему Расширенная матрица системы

1-я итерация. За направляющий элемент берем

Вторая итерация. Выбираем направляющий элемент

Третья итерация. Берем за направляющий элемент

Исходная система равносильна следующей: Общее решение имеет вид:

Метод Жордана –Гаусса в excel. Открыть окно и установить «Поиск решения».

Функции МУМНОЖ—умножение матриц ТРАНСП—транспонирование МОПРЕД—вычисление определителя МОБР—вычисление обратной

Решить в excel систему Мы уже видели, что эта система

Следующее действие Нажимаем одну за другой клавиши F2+Ctrl+Shift+Enter.

Нажимаем клавиши F2+Ctrl+Shift+Enter. Получили первое базисное решение ,

Слайды презентации

Слайд 2 Содержание
Элементы линейной алгебры
Задачи линейного программирования
Графический метод решения ЗЛП
Симплексный

метод решения ЗЛП
Двойственные задачи
Транспортная задача
Анализ временных рядов

Слайд 3 Элементы линейной алгебры
Лекция 1

Слайд 4 Определители
Определение. Определителем 2-го порядка

называется выражение

(1)

Числа , , , называются элементами определителя. Они расположены в двух строках и двух столбцах. Определитель 2-го порядка равен разности произведений его элементов главной и побочной диагоналей.

Слайд 5
Определителем 3-го порядка называется выражение

Слайд 6 Правило треугольника
Способ вычисления определителей 3-го порядка
называется

Правило треугольника Способ вычисления определителей 3-го порядка называется правилом треугольника. Элементы,

правилом треугольника.
Элементы, входящие в определитель со знаком +

и со знаком –, выбираются из определителя, как показано на рисунках.

Слайд 7 Пример
Найдем определитель

Слайд 8 Ранг матрицы.
Рассмотрим матрицу А размера

.

Выберем в этой матрице произвольно k строк и k столбцов, где k ≤ m и k≤ n. Из элементов, стоящих на пересечении выделенных k строк и k столбцов, составим определитель k-го порядка. Все такие определители называют минорами k-го порядка матрицы А.

Слайд 9
Определение. Наивысший порядок отличного от нуля

минора матрицы называется ее рангом.
Для вычисления

ранга матрицы ее сначала приводят к более простому виду с помощью так называемых элементарных преобразований, к которым относятся:
1)перестановка строк матрицы;
2)умножение какой-либо строки на одно и то же отличное от нуля число;
3)прибавление к элементам строки соответствующих элементов другой строки, предварительно умноженных на некоторое число.

Слайд 10
Можно показать, что элементарные преобразования не

Можно показать, что элементарные преобразования не меняют ранга матрицы. Если

меняют ранга матрицы.
Если с помощью элементарных преобразований

получить нули ниже главной диагонали матрицы, то ранг исходной матрицы будет равен числу ненулевых строк преобразованной матрицы.

Слайд 11 Пример
С помощью элементарных преобразований вычислить

ранг матрицы

Слайд 12 Система m линейных уравнений с n неизвестными

Рассмотрим систему m линейных уравнений с n неизвестными:

Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца свободных членов, называют расширенной матрицей:

Слайд 13

Для того чтобы система линейных уравнений

была совместной, необходимо и достаточно, чтобы ранг матрицы системы

был равен рангу ее расширенной матрицы.
Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.

Слайд 14 Метод Гаусса решения систем линейных уравнений
Для того

чтобы решить систему уравнений

выписывают расширенную матрицу этой

системы

Слайд 15
Назовем матрицей системы матрицу, составленную из

коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца

свободных членов, называют расширенной матрицей:

Слайд 16 Элементарные преобразования
Для того чтобы решить систему

уравнений выписывают расширенную матрицу этой системы и над строками

этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы

будут располагаться нули.

Слайд 17
Разрешается:
1) изменять порядок строк

матрицы, что соответствует изменению порядка уравнений;
2) умножать строки

на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа;
3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.

Слайд 18 Пример
Решить систему

Слайд 19 Общее решение системы линейных уравнений
Определение. Если

ранг матрицы равен ,

то любой отличный от нуля минор порядка этой матрицы называется базисным.
Решить систему уравнений

Слайд 20 Пример
Решить систему

Расширенная матрица этой системы имеет

вид

Минор 3-го порядка в левой части матрицы-

базисный. Он равен единице.

Слайд 21
Переменные

Переменные -базисные, а остальные –свободные. Их

-базисные, а остальные –свободные. Их находят,

перенося свободные неизвестные в правые части уравнений.
Обозначим Тогда

Слайд 22 Метод Жордана –Гаусса решения СЛАУ
Решаем систему уравнений

Слайд 23
В процессе решения могут встретиться следующие

случаи :
1) в результате преобразования получилась матрица вида

В этом случае система совместная,
определенная и имеет единственное решение

Слайд 24
2)на некотором этапе получилась матрица , содержащая

единичных столбцов. Например,

..

Тогда система совместна и имеет бесчисленное множество решений. Общее решение можно записать в виде

Слайд 25

Придавая каждой из стоящих

Придавая каждой из стоящих в правых частях равенств свободных

в правых частях равенств свободных переменных произвольные значения, получаем

частные решения системы.
Базисным решением СЛАУ называется частное решение . в котором свободные переменные имеют нулевые значения:
.

Слайд 26 Пример.
Решить методом Жордана-Гаусса систему

Расширенная матрица

системы

Слайд 27
1-я итерация. За направляющий элемент берем

. Преобразуем 1-ый столбец

в единичный. Для этого прибавим ко 2-й и 3-й строкам 1-ю, умноженную на -1. Получим матрицу

Слайд 28
Вторая итерация. Выбираем направляющий элемент

Вторая итерация. Выбираем направляющий элемент Т.к. он

Т.к. он отличен от

нуля, то разделим третью строку на -1 и преобразуем второй столбец в единичный. Для этого к первой строке прибавим третью, умноженную на -2. Получим

Слайд 29
Третья итерация. Берем за направляющий элемент

Третья итерация. Берем за направляющий элемент Т.к. он

Т.к. он отличен от нуля,

то разделим вторую строку на -1. Преобразуем третий столбец в единичный. Для этого умножим вторую строку на -1 и прибавим к третьей. Получим матрицу

Слайд 30
Исходная система равносильна следующей:

Общее

решение имеет вид:

Переменные

являются базисными, остальные – свободными. Если свободные переменные положить равными нулю, т.е. , то получим первое базисное решение (1,3,2,0,0).

Слайд 31 Метод Жордана –Гаусса в excel.
Открыть окно

и установить «Поиск решения».
В меню :Сервис /Надстройки/

Поиск решения (ставим галочку).вычисления производим с помощью функций Нажимаем кнопки Вставка, функции. В окне Мастер функций выбираем нужную.

Слайд 32 Функции
МУМНОЖ—умножение матриц
ТРАНСП—транспонирование

Функции МУМНОЖ—умножение матриц ТРАНСП—транспонирование МОПРЕД—вычисление определителя МОБР—вычисление обратной матрицы Функции

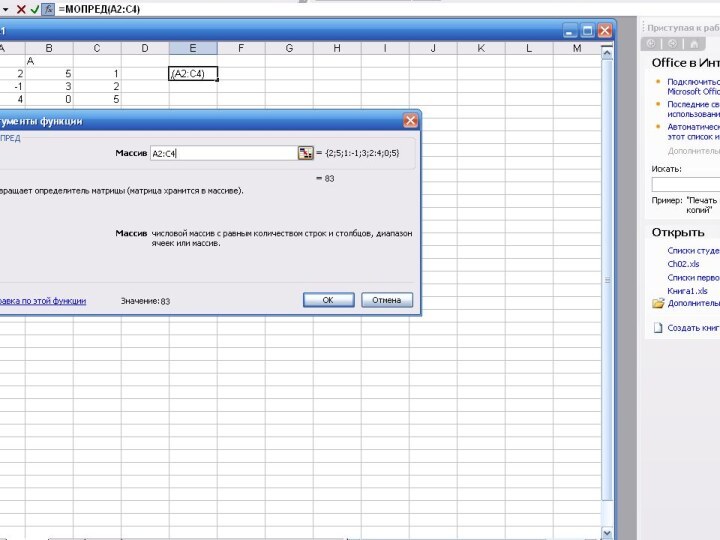
МОПРЕД—вычисление определителя
МОБР—вычисление обратной матрицы
Функции для

выполнения действий с матрицами находятся в категории МАТЕМАТИЧЕСКИЕ.
Если определитель обратной матрицы равен нулю, то при вычислении ее появляется знак ошибки #число!

Слайд 33

Слайд 34 Вычислить определитель

#число!

Слайд 35

Слайд 36 Решить в excel систему

Слайд 37 Решить в excel систему
Мы уже

видели, что эта система имеет множество решений, причем нами

уже найдено одно базисное решение. Общее число базисных решений будет не более, чем

Здесь число 5 –это число всех переменных, а 3-число базисных переменных. Рассмотрим по шагам получение всех базисных решений, начиная с первого