Слайд 2
Цели урока:
Определение квадратного уравнения
Виды квадратных уравнений
Способы решения квадратных
уравнений:
1) Разложение левой части уравнения на множители
2)Решение квадратных
уравнений по формуле
3)Решение уравнений с использованием теоремы Виета
4)Решение уравнений способом переброски
5)Свойства коэффициентов квадратного уравнения
6) Графическое решение квадратного уравнения
7) Решение квадратных уравнений с помощью циркуля и линейки
8) Решение квадратных уравнений с помощью номограммы
Слайд 3
Определение квадратного уравнения
Квадратное уравнение – алгебраическое
уравнение общего вида
ax2+bx+c = 0,
где x - свободная переменная,
a,b,c – коэффициенты, причём a ≠ 0.
Выражение ax2+bx+c называют квадратным трёхчленом, а элементы квадратного уравнения имеют собственные названия:
a называют первым или старшим коэффициентом,
b называют вторым, средним или коэффициентом при x,
c называют свободным членом.
Слайд 4
Виды квадратных уравнений
Квадратные уравнения могут быть:
Полными
- это квадратное уравнение, все коэффициенты которого отличны от
нуля.
Неполными - это квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Приведёнными - это квадратное уравнение, в котором старший коэффициент равен единице.
Слайд 5
Например:
Полное квадратное уравнение:
ax2+bx+c=0,
где коэффициенты b и с отличны от нуля;
Неполное квадратное уравнение:
ax2+bx=0, ax2+c=0 или ax2=0
т.е. хотя бы один из коэффициентов b или c равен нулю;
Приведённое квадратное уравнение:
x2+bx+c=0,
т.е. уравнение, первый коэффициент которого равен единице (а=1)
Слайд 6
Способы решений квадратных уравнений
1. Разложение левой части уравнения
на множители
Решим уравнение х + 10х –
24 = 0.
Разложим левую часть уравнения на множители:
х + 10х – 24 = х + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + +12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и - 12 являются корнями уравнения х + 10х – 24 = 0.
Слайд 8
4х – 4х + 1 = 0,
а =4,
b = - 4, с = 1.
D =
b – 4ас= 16 – 4∙4∙1 = 0,
D = 0, один корень;
х =
2х² +3х + 4 = 0
а =2, b= 3, с = 4
D = b – 4ас=9 – 4∙2∙4 =9 – 32 =
- 13
D < 0. Уравнение не имеет корней.
Слайд 9
3.Решение уравнений с использованием теоремы Виета
(прямой и обратной)
Как
известно, приведенное квадратное уравнение имеет вид:
х² + px
+ q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид:
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
Теорема Виета для квадратного уравнения ах +вх +с = 0 имеет вид:
Слайд 11
Решим уравнение 2х² – 11х + 15 =
0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим
уравнение у² – 11y +30 = 0.
Согласно теореме Виета:
Слайд 13
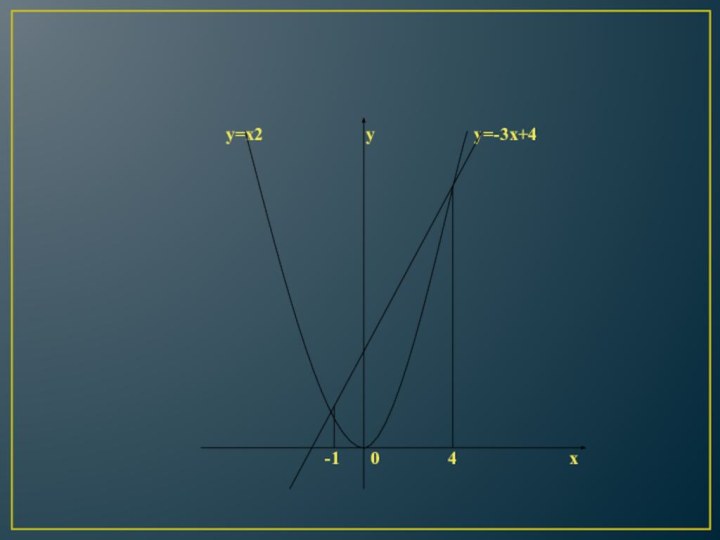
6.Графическое решение квадратного уравнения
Решим графически уравнение
х²
– 3х – 4 = 0.
Запишем уравнение в
виде
х² = 3х + 4 .
Построим параболу у = х² и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и х2 = 4.
Слайд 17
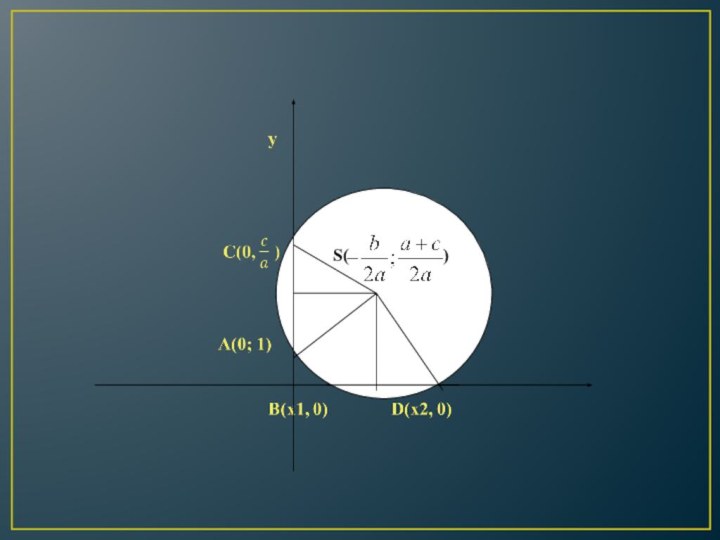
Решим графически уравнение х² – 2х – 3
= 0.
Определим координаты точки центра окружности по формулам
х
= -
у = =
Проведем окружность радиуса S A, где А (0;1).
Ответ: х1 = – 1 , х2 = 3
Слайд 18
8.Решение квадратных уравнений с помощью номограммы
Это старый и
незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83
(см. Брадис В.М. Четырехзначные математические таблицы. – М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z²+pz+q=0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Слайд 19
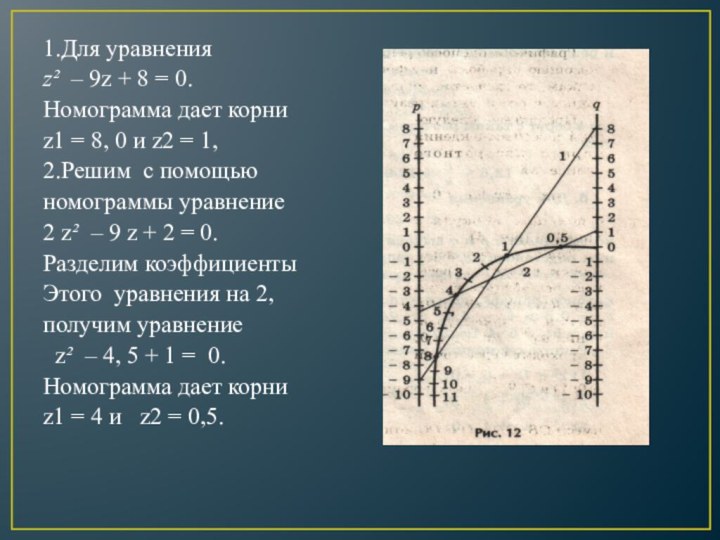
1.Для уравнения
z² – 9z + 8 =
0.
Номограмма дает корни
z1 = 8, 0 и
z2 = 1,
2.Решим с помощью
номограммы уравнение
2 z² – 9 z + 2 = 0.
Разделим коэффициенты
Этого уравнения на 2,
получим уравнение
z² – 4, 5 + 1 = 0.
Номограмма дает корни
z1 = 4 и z2 = 0,5.
Слайд 20
3. Для уравнения
z² + 5 z – 6
= 0
номограмма дает положительный
корень z1 = 1,0, а отрицательный
корень
находим, вычитая
положительный корень
из – р, т.е. z2 = – р – 1 =
= – 5 – 1 = – 6,0 (рис.13.)
4. Для уравнения
z² – 2z – 8 = 0
номограмма дает положительный
корень z1 = 4,0, отрицательный
равен z2 = – р – z1 = 2 – 4 = – 2,0.