Слайд 2
Содержание :
Числовая последовательность.
Арифметическая прогрессия.
Геометрическая прогрессия.
Слайд 3
Числовая последовательность
Слайд 4
В повседневной практике часто используется нумерация различных предметов,
чтобы указать порядок их расположения. Например, в сберегательном банке
по номеру лицевого счета вкладчика можно легко найти этот счет и посмотреть, какой вклад на нем лежит. Пусть на счете № 1 лежит вклад a 1 рублей, на счете № 2 лежит вклад a 2 рублей и т. д. Получается числовая последовательность
a 1,a 2,a 3…,a N
где N — число всех счетов. Здесь каждому натуральному числу n от 1 до N поставлено в соответствие число a N
Слайд 5
В математике изучаются бесконечные числовые последовательности :
a 1,a
2,a 3…,a N
Число a 1 называют первым членом последовательности,
число a 2— вторым членом последовательности, число a 3— третьим членом последовательности и т. д.
Число a N называют n-м (энным) членом последовательности, а натуральное число n — его номером.
Слайд 6
Задача 1.
Числовая последовательность задана формулой а
n = n (n - 2). Вычислить сотый член
этой последовательности.
Решение:
a 100=100 (100 - 2) = 9800.
Ответ:9800.
Слайд 7
Задача 2.
Числовая последовательность задана формулой
x n= 2n + 3. Найти номер члена последовательности,
равного: 1) 43; 2) 50.
Решение:
1) По условию 2n + 3 = 43, откуда n = 20.
2) 2n + 3 = 50, откуда n = 23,5. Так как искомый номер — натуральное число, то в данной последовательности нет члена, равного 50.
Ответ:1)20 ; 2)50.
Слайд 9
Числовая последовательность
а 1, а 2, а 3,
…, а n, .…
называется арифметической прогрессией, если для
всех натуральных n выполняется равенство
a n+1= а n+d,
где d – некоторое число.
Из этой формулы следует, что а n+1 – а n =d. Число d называют разностью арифметической прогрессии.
Натуральный ряд чисел 1, 2, 3, 4, ..., n,
... является арифметической прогрессией. Разность этой прогрессии d = 1.
2) Последовательность целых отрицательных чисел -1, -2, -3, ..., -n, ... — арифметическая прогрессия с разностью d = -1.
3) Последовательность 3, 3, ..., 3, ... —арифметическая прогрессия с разностью d = 0.
Слайд 11
каждый член арифметической прогрессии, начиная со второго, равен
среднему арифметическому двух соседних с ним членов. Этим объясняется
название «арифметическая» прогрессия.
Слайд 12
Формула n-го члена арифметической прогрессии:
an = a1 +
(n-1)d (1)
Слайд 13
Задача 1.
Найти сотый член арифметической прогрессии, если первый
её член равен -6 и d = 4.
►
По формуле (1) имеем
а100 = -6 + (100-1) * 4 = 390.
Слайд 14
Задача 2.
Число 99 является членом арифметической прогрессии 3,
5, 7, 9, ... Найти номер этого члена.
► Пусть
n — искомый номер. Так как
а1 = 3 и d = 2, то по формуле (1) имеем
99 = 3 + (n - 1) 2.
Поэтому 99 = 3 + 2n - 2; 98 = 2n, n = 49.
Ответ : n = 49.
Слайд 15
Задача 3.
В арифметической прогрессии а8 = 130 и
а12 = 166. Найти формулу n-го члена.
► Используя формулу
(1), находим:
а8 = а1 + 4d, а12 = а1 + 11d.
Подставив данные значения а8 и а12, получим систему уравнений относительно а1 и d:
Слайд 16
Вычитая из второго уравнения первое, получаем:
4d= 36, d
= 9. Следовательно,
а1 = 130 - 7d = 130
- 63 = 67.
Запишем формулу n-го члена прогрессии:
аn = 67 + 9 (n - 1) = 67 + 9n - 9 = 58 + 9n.
Ответ : аn = 9n + 58.
Слайд 17
Сумма n первых членов арифметической прогрессии
Слайд 18
Задача
Найти сумму 38 + 35 + 32 +
... + (-7), если известно, что ее слагаемые являются
последовательными членами арифметической прогрессии.
► По условию а1 = 38, d = -3, аn = -7.
Применяя формулу аn = а1 + (n – 1)d, получаем
-7 = 38 + (n - 1) (-3), откуда n = 16.
По формуле (2) находим: S16 = 248.
Слайд 20
Числовая последовательность b1, b2, b3, ..., bn, ...
называется
геометрической прогрессией, если для всех натуральных n выполняется равенство
bn+1=bnq ,
где bn ≠ 0, q — некоторое число, не равное нулю.
Из этой формулы следует, что
Число q называется знаменателем геометрической прогрессии.
Слайд 21
Если все члены прогрессии положительны, то
т. е.
каждый член геометрической прогрессии, начиная со второго, равен среднему
геометрическому двух соседних с ним членов. Этим объясняется название «геометрическая» прогрессия.
Слайд 22
Сумма n первых членов геометрической прогрессии (со знаменателем
q≠1)
Формула n-го члена геометрической прогрессии.
Слайд 23
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее
знаменателя меньше единицы.
Слайд 24
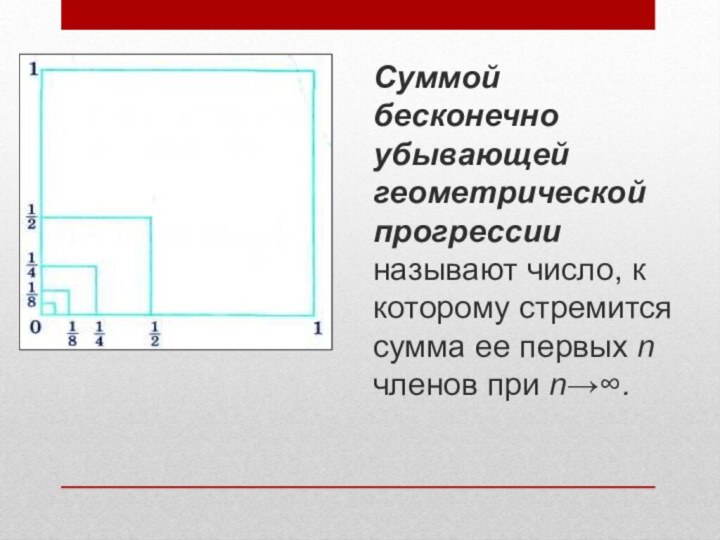
Суммой бесконечно убывающей геометрической прогрессии называют число, к
которому стремится сумма ее первых n членов при n→∞.
Слайд 25
Сумма бесконечно убывающей геометрической прогрессии