- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задания по функциям
Содержание
- 2. Область определения функции Рекомендуемое время исполнения 45
- 3. Область определения функции Рекомендуемое время исполнения 45
- 4. Область определения функции Рекомендуемое время исполнения 45
- 5. Область определения функции Ответ номер 3 А1
- 6. Область определения функции Чтобы выполнить пример, нужно
- 7. Область определения функции 2 Найдите область
- 8. Область определения функции Рекомендуемое время исполнения 45
- 9. Область определения функции Рекомендуемое время исполнения 45
- 10. Область определения функции Рекомендуемое время исполнения 45
- 11. Область определения функции Ответ номер 3 2
- 12. Область определения функции Чтобы выполнить пример, нужно
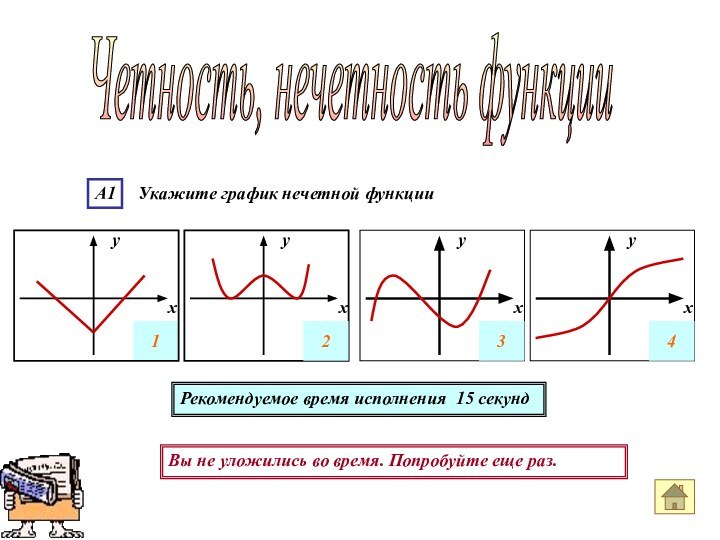
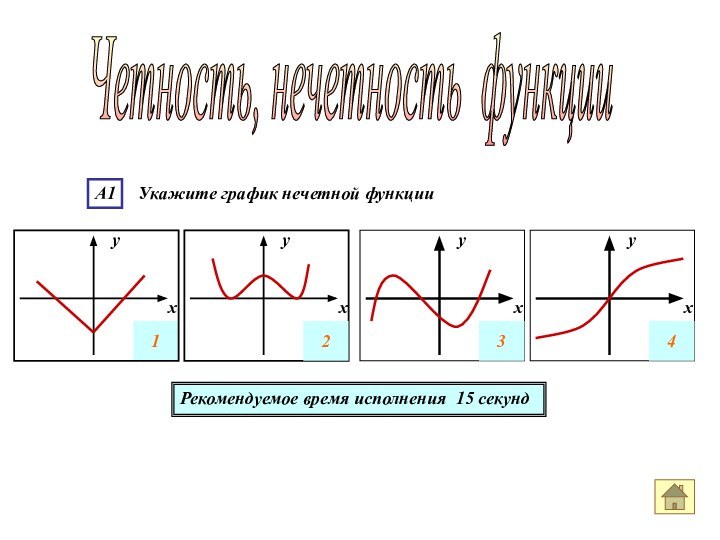
- 13. А1 Укажите график нечетной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции
- 14. 1А1 Укажите график нечетной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции 432
- 15. 1А1 Укажите график нечетной функцииРекомендуемое
- 16. 1А1 Укажите график нечетной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции 432
- 17. 1А1 Укажите график нечетной функцииЧетность, нечетность функции 432Ответ номер 4
- 18. 1А1 Укажите график нечетной функцииЧетность,
- 19. А2 Укажите график четной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции
- 20. А2 Укажите график четной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции 1432
- 21. А2 Укажите график четной функцииРекомендуемое
- 22. А2 Укажите график четной функцииРекомендуемое время исполнения 15 секундЧетность, нечетность функции 1432
- 23. А2 Укажите график четной функцииЧетность, нечетность функции Ответ номер 21432
- 24. А2 Укажите график четной функцииЧетность,
- 25. Четность, нечетность функции Рекомендуемое время исполнения 25 секунд
- 26. Четность, нечетность функции Рекомендуемое время исполнения 25
- 27. Рекомендуемое время исполнения 45 секундВы не уложились
- 28. Рекомендуемое время исполнения 45 секундЧетность, нечетность функции
- 29. Ответ номер 2 Четность, нечетность функции 1)
- 30. Четность, нечетность функции Ответ номер 2 График
- 31. Рекомендуемое время исполнения 15 секундСвойства функций
- 32. Свойства функций Рекомендуемое время исполнения 15 секунд1)
- 33. Вы не уложились во время. Попробуйте еще
- 34. Свойства функций Рекомендуемое время исполнения 15 секунд1)
- 35. Свойства функций Ответ номер 3 1)
- 36. Ответ номер 3Свойства функций Часть графика, где
- 37. Рекомендуемое время исполнения 15 секундСвойства функций
- 38. Свойства функций Рекомендуемое время исполнения 15 секунд1)
- 39. Вы не уложились во время. Попробуйте еще
- 40. Свойства функций Рекомендуемое время исполнения 15 секунд1)
- 41. Свойства функций Ответ номер 41) [-3;2]
- 42. Ответ номер 4Свойства функций Для определения промежутков
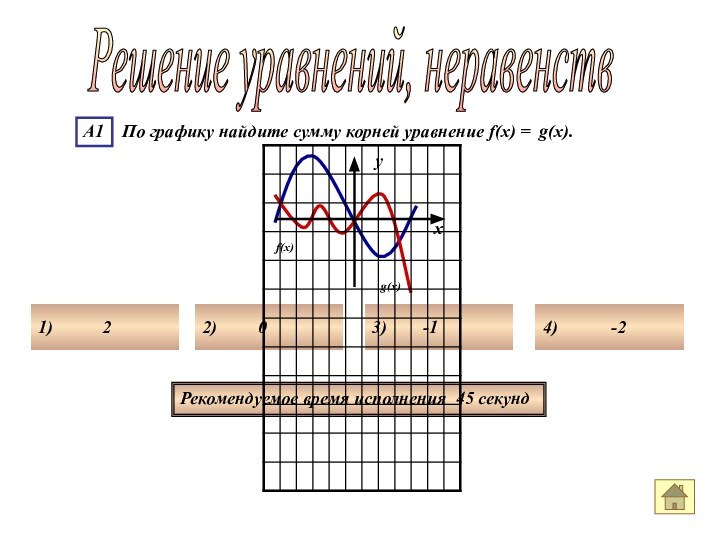
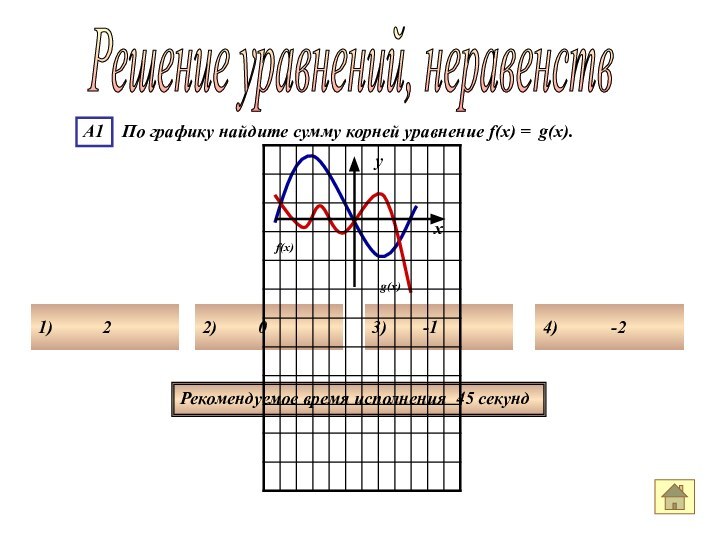
- 43. Рекомендуемое время исполнения 45 секундРешение уравнений, неравенств
- 44. Решение уравнений, неравенств Рекомендуемое время исполнения 45
- 45. Вы не уложились во время. Попробуйте еще
- 46. Решение уравнений, неравенств Рекомендуемое время исполнения 45
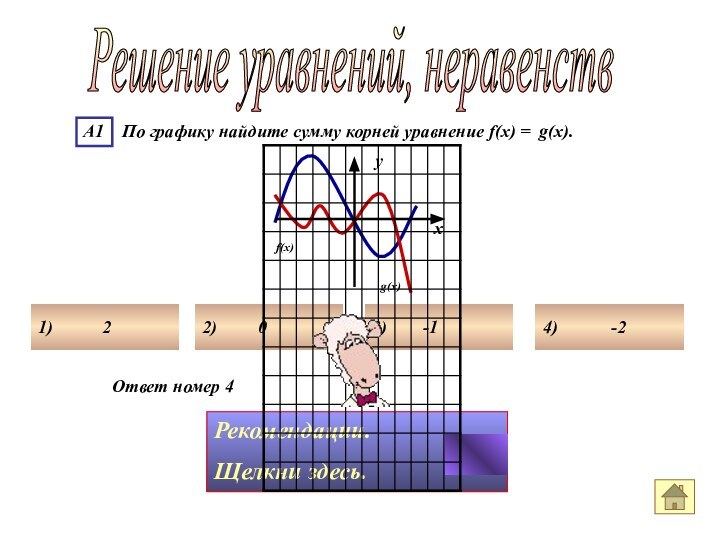
- 47. Ответ номер 4Решение уравнений, неравенств 1)
- 48. Ответ номер 4Решение уравнений, неравенств Чтобы найти
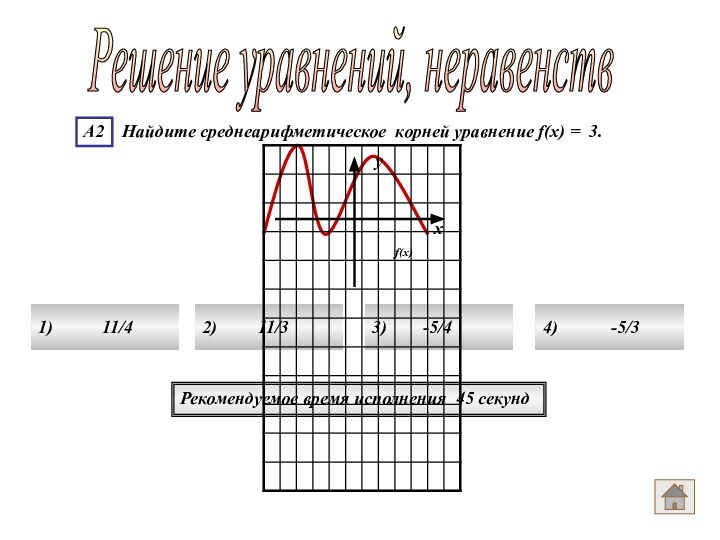
- 49. Рекомендуемое время исполнения 45 секундРешение уравнений, неравенств f(x) ух
- 50. Решение уравнений, неравенств Рекомендуемое время исполнения 45
- 51. Вы не уложились во время. Попробуйте еще
- 52. Решение уравнений, неравенств Рекомендуемое время исполнения 45
- 53. Ответ номер 3Решение уравнений, неравенств 1)
- 54. Ответ номер 3Решение уравнений, неравенств Решением уравнения
- 55. Рекомендуемое время исполнения 45 секундРешение уравнений, неравенств
- 56. Ответ номер 4Решение уравнений, неравенств 1)
- 57. Ответ номер 4Решение уравнений, неравенств Чтобы найти
- 58. Рекомендуемое время исполнения 45 секундРешение уравнений, неравенств f(x) ух
- 59. Решение уравнений, неравенств Рекомендуемое время исполнения 45
- 60. Вы не уложились во время. Попробуйте еще
- 61. Решение уравнений, неравенств Рекомендуемое время исполнения 45
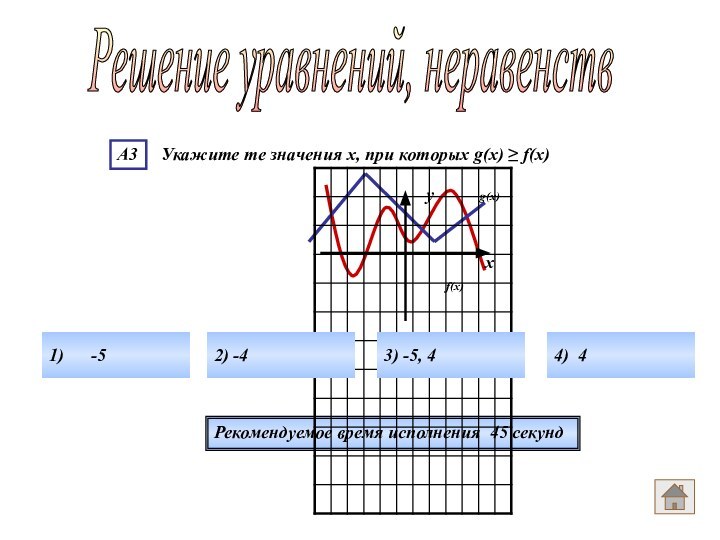
- 62. 1) -5 2) -4 3)
- 63. Ответ номер 2Решение уравнений, неравенств Для того,
- 64. Рекомендуемое время исполнения 45 секундРешение уравнений, неравенств
- 65. Решение уравнений, неравенств Рекомендуемое время исполнения 45 секунд1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)
- 66. Вы не уложились во время. Попробуйте еще
- 67. Решение уравнений, неравенств Рекомендуемое время исполнения 45 секунд1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)
- 68. Ответ номер 4Решение уравнений, неравенств 1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)
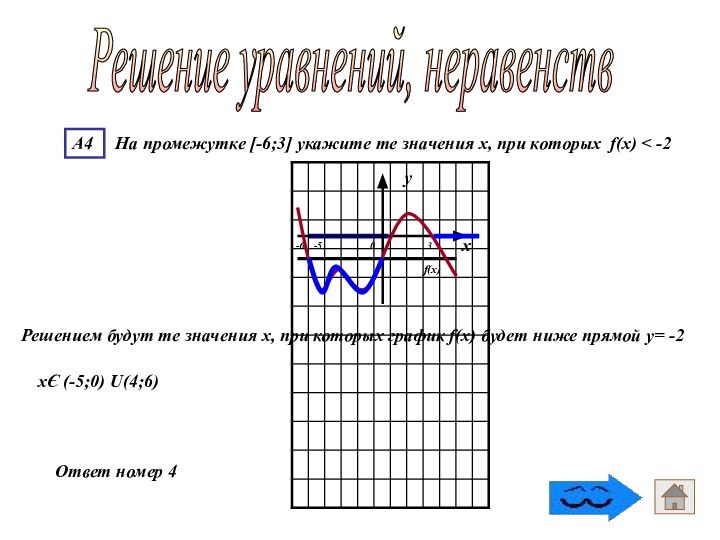
- 69. Ответ номер 4Решение уравнений, неравенств Решением будут
- 70. Множество значений функции Рекомендуемое время исполнения 45 секунд
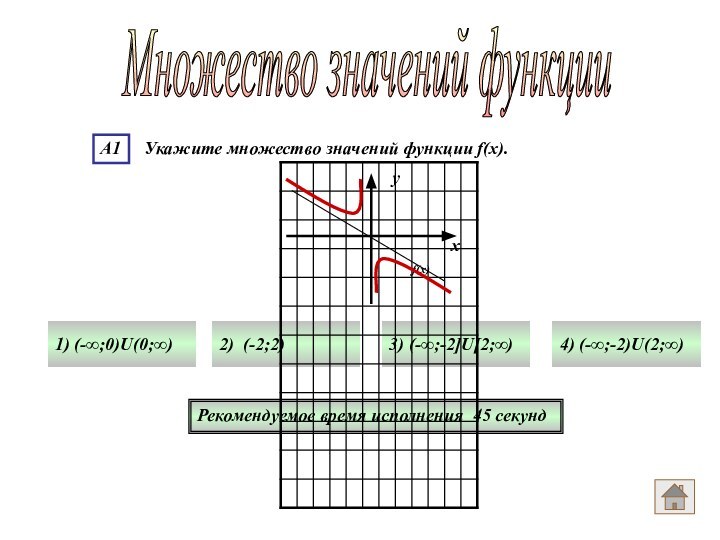
- 71. Множество значений функции Рекомендуемое время исполнения 45 секунд1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)
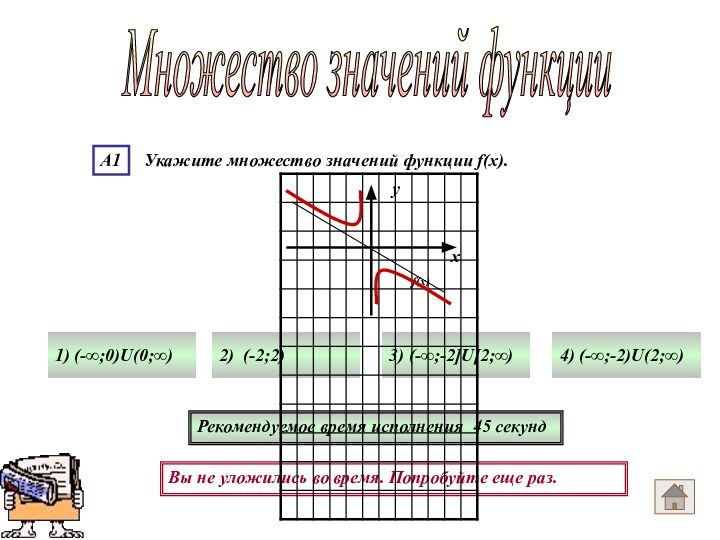
- 72. Вы не уложились во время. Попробуйте еще
- 73. Множество значений функции Рекомендуемое время исполнения 45 секунд1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)
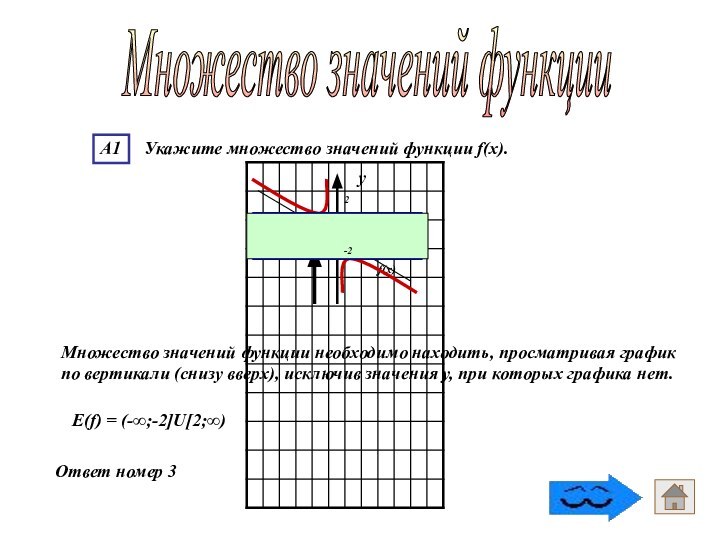
- 74. Ответ номер 3Множество значений функции 1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)
- 75. Скачать презентацию
- 76. Похожие презентации























![Задания по функциям Свойства функций Рекомендуемое время исполнения 15 секунд1) [-3;2]](/img/tmb/11/1044255/d6247ab0f270631aa58058026564a837-720x.jpg)
![Задания по функциям Свойства функций Рекомендуемое время исполнения 15 секунд1) [-3;2]](/img/tmb/11/1044255/94fe11f1e67f45d573199dbdab12fe09-720x.jpg)
![Задания по функциям Свойства функций Ответ номер 41) [-3;2] 2) (-3;-1,5)U(2;∞)3)](/img/tmb/11/1044255/499569a7994627691b8551b6a5214bae-720x.jpg)










![Задания по функциям Решение уравнений, неравенств Рекомендуемое время исполнения 45 секунд1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)](/img/tmb/11/1044255/063bfc85d7f58e0ce6e6b9ca322bce0e-720x.jpg)

![Задания по функциям Решение уравнений, неравенств Рекомендуемое время исполнения 45 секунд1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)](/img/tmb/11/1044255/c606ba5303d314479f07592e24d8a76e-720x.jpg)
![Задания по функциям Ответ номер 4Решение уравнений, неравенств 1) [-5;-2] 2) (-4,5;-2]3) (-∞;-5)U(0;3)4) (-5;0) U(4;6)](/img/tmb/11/1044255/74e5773bb85710e99cece700ed245c53-720x.jpg)
![Задания по функциям Множество значений функции Рекомендуемое время исполнения 45 секунд1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)](/img/tmb/11/1044255/d3127d1bbde6cdad8e1610bb6b482deb-720x.jpg)
![Задания по функциям Множество значений функции Рекомендуемое время исполнения 45 секунд1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)](/img/tmb/11/1044255/145cc396c3058595600d8610fa3afa1f-720x.jpg)
![Задания по функциям Ответ номер 3Множество значений функции 1) (-∞;0)U(0;∞) 2) (-2;2)3) (-∞;-2]U[2;∞)4) (-∞;-2)U(2;∞)](/img/tmb/11/1044255/f10c206a47235030c082735f95097c26-720x.jpg)
Слайд 3
Область определения функции
Рекомендуемое время исполнения 45 секунд
Вы
не уложились во время. Попробуйте еще раз.
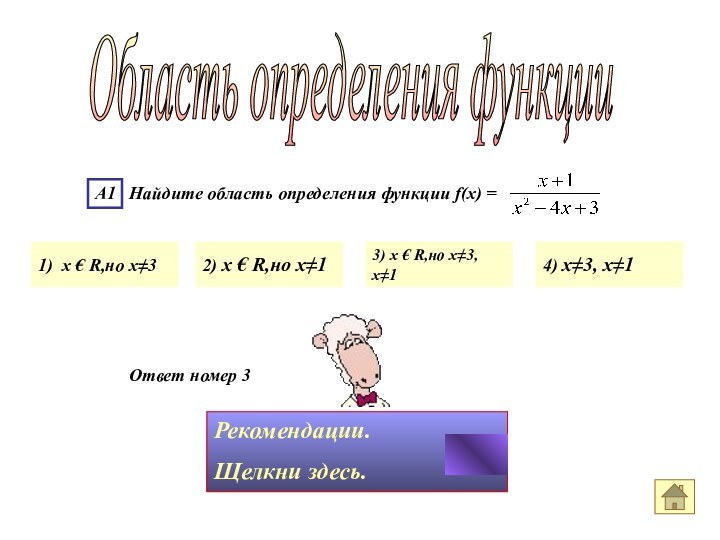
А1 Найдите
область определения функции f(x) =
Слайд 4
Область определения функции
Рекомендуемое время исполнения 45 секунд
А1
Найдите область определения функции f(x) =
Слайд 6
Область определения функции
Чтобы выполнить пример, нужно определить
какие виды «запретов» имеет функция.
Первый запрет: корень четной
степени Второй запрет: знаменатель не равен нулю
Следовательно,
хЄ R, но х ≠ 1, х ≠ 3
Ответ номер 3
х2 – 4х + 3 = 0. х = 1, х = 3
А1 Найдите область определения функции f(x) =
Слайд 7
Область определения функции
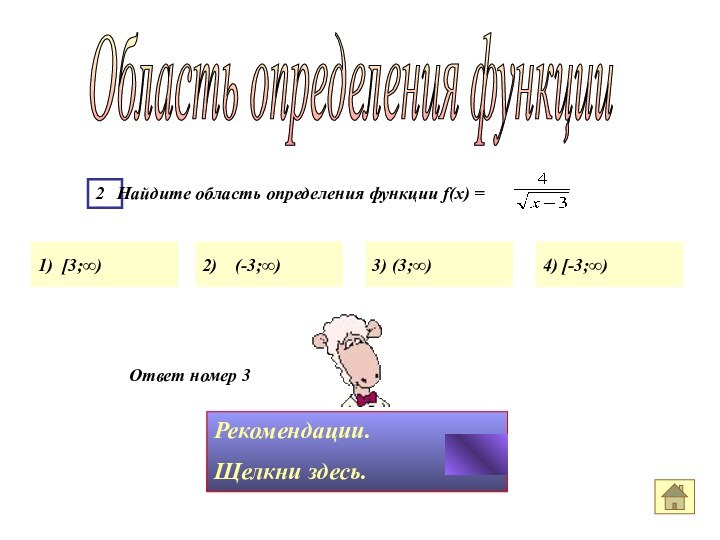
2 Найдите область определения
функции f(x) =
Рекомендуемое время исполнения
45 секунд
Слайд 8
Область определения функции
Рекомендуемое время исполнения 45 секунд
2
Найдите область определения функции f(x) =
Слайд 9
Область определения функции
Рекомендуемое время исполнения 45 секунд
Вы
не уложились во время. Попробуйте еще раз.
2 Найдите
область определения функции f(x) =
Слайд 10
Область определения функции
Рекомендуемое время исполнения 45 секунд
2
Найдите область определения функции f(x) =
Слайд 12
Область определения функции
Чтобы выполнить пример, нужно определить
какие виды «запретов» имеет функция.
Первый запрет: корень четной
степени Второй запрет: знаменатель
Следовательно,
хЄ (0;∞)
Ответ номер 3
2 Найдите область определения функции f(x) =
Слайд 13
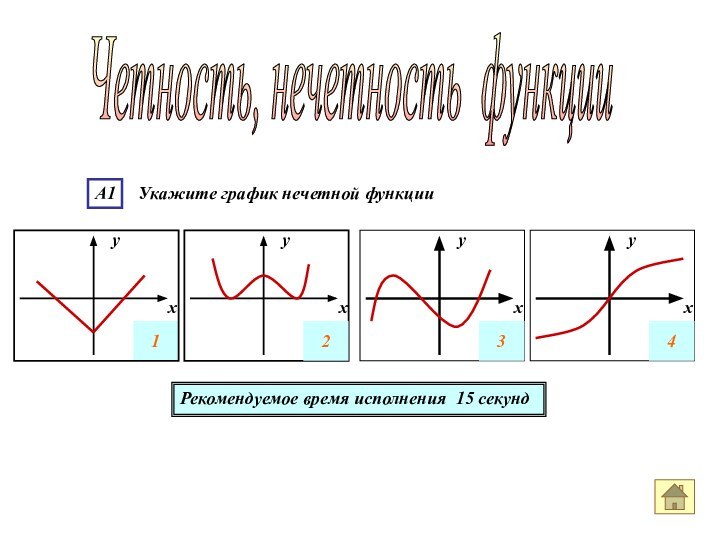
А1 Укажите график нечетной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
Слайд 14
1
А1 Укажите график нечетной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
4
3
2
Слайд 15
1
А1 Укажите график нечетной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
4
3
2
Вы не уложились во
время. Попробуйте еще раз.
Слайд 16
1
А1 Укажите график нечетной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
4
3
2
Слайд 18
1
А1 Укажите график нечетной функции
Четность, нечетность
функции
3
2
График нечетной функции симметричен относительно начала координат.
Симметрия относительно
начала координат наблюдается только у графика 4.Ответ номер 4
Слайд 19
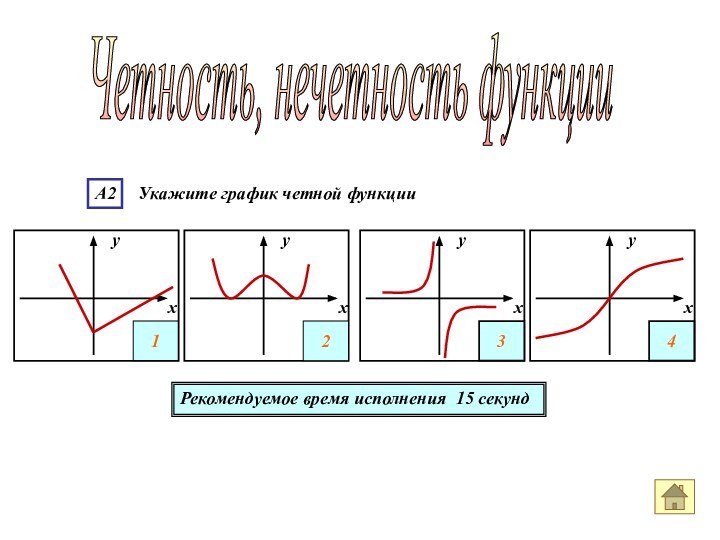
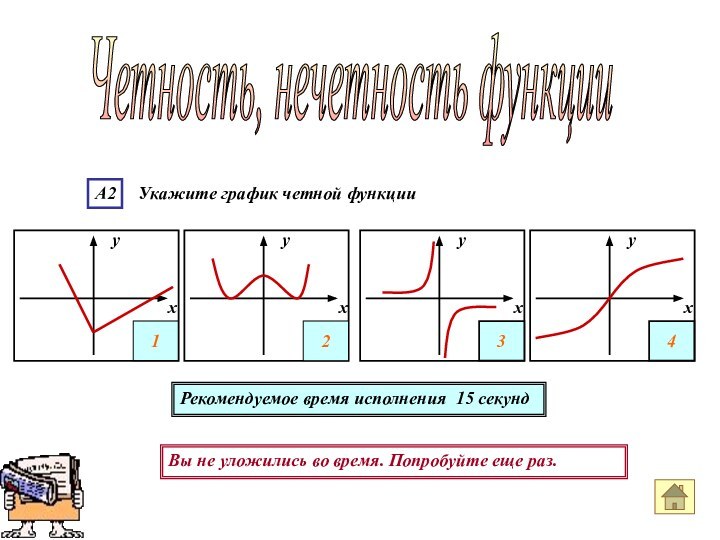
А2 Укажите график четной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
Слайд 20
А2 Укажите график четной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
1
4
3
2
Слайд 21
А2 Укажите график четной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
Вы не уложились во
время. Попробуйте еще раз.1
4
3
2
Слайд 22
А2 Укажите график четной функции
Рекомендуемое время
исполнения 15 секунд
Четность, нечетность функции
1
4
3
2
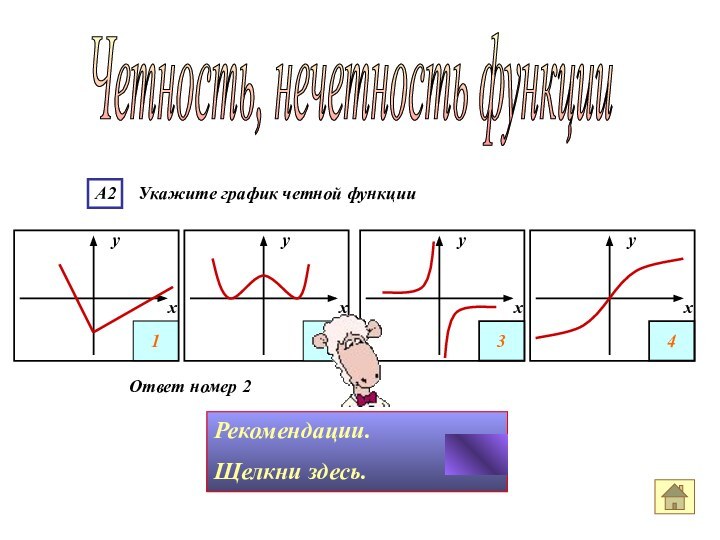
Слайд 24
А2 Укажите график четной функции
Четность, нечетность
функции
График четной функции симметричен относительно оси ОУ.
Симметрия относительно
оси ОУ наблюдается только у графика 2.Ответ номер 2
1
4
3
Слайд 27
Рекомендуемое время исполнения 45 секунд
Вы не уложились во
время. Попробуйте еще раз.
Четность, нечетность функции
1)
6
2) 7
3) 5
4) 3
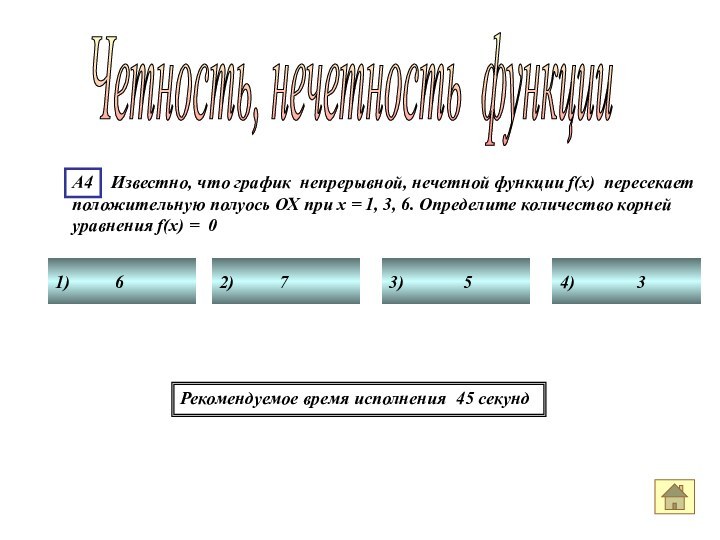
Слайд 30
Четность, нечетность функции
Ответ номер 2
График непрерывной,
нечетной функции f(x) проходит через начало координат и симметричен
относительно начала координат.Следовательно, если уравнение f(x) = 0 имеет корень х = х0 , то уравнение имеет корень и х = - х0 . Так как график проходит через начало координат, то
х = 0 является корнем уравнения.
Наше уравнение имеет корни х = 1, х = 3, х = 6, следовательно имеет корни х = -1, х = -3, х = -6. В силу непрерывности функции, график проходит через начало координат, следовательно, х = 0 – корень уравнения.
Всего корней 7.
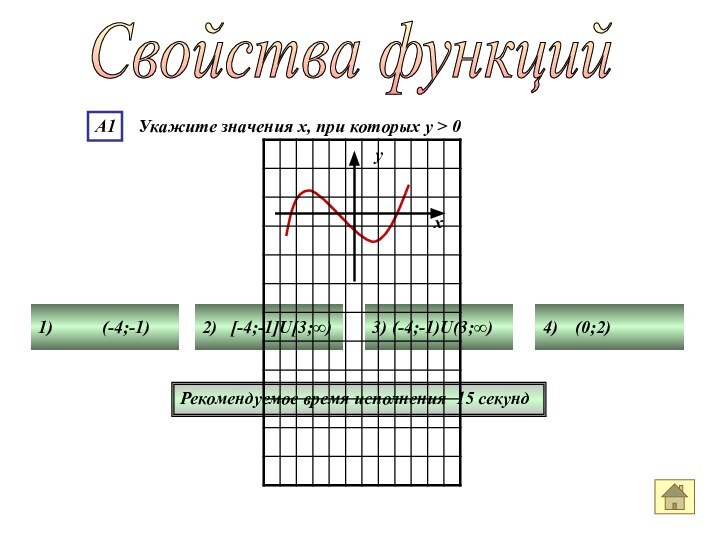
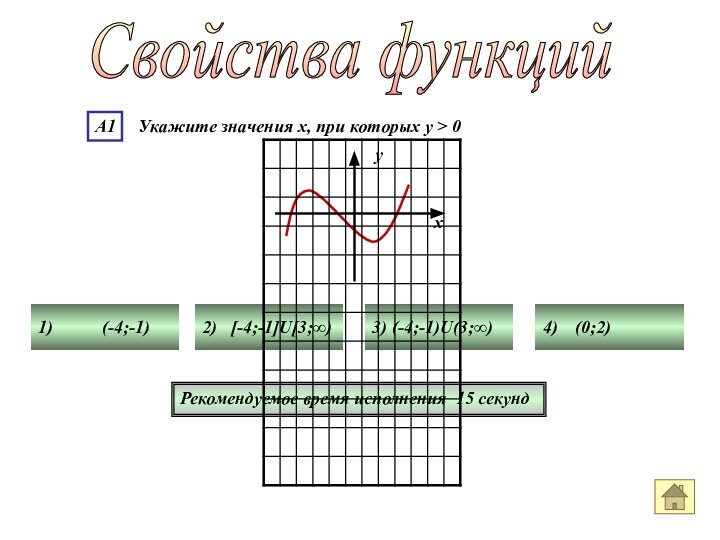
Слайд 32
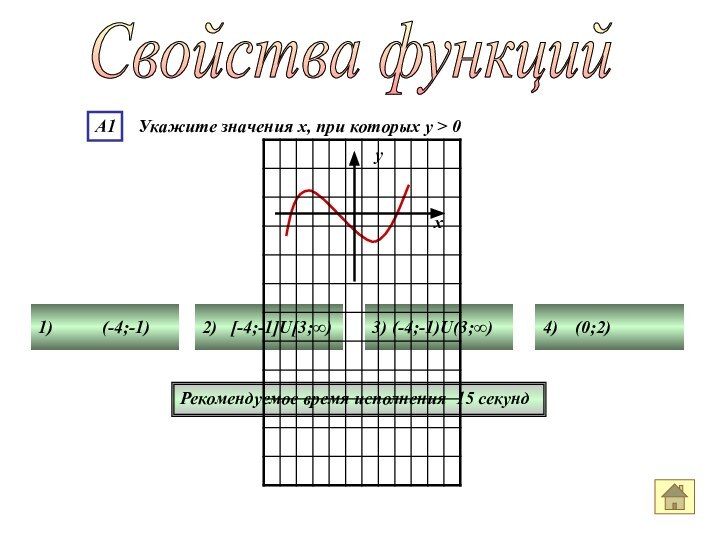
Свойства функций
Рекомендуемое время исполнения 15 секунд
1)
(-4;-1)
2) [-4;-1]U[3;∞)
3)
(-4;-1)U(3;∞) 4) (0;2)
Слайд 33
Вы не уложились во время. Попробуйте еще раз.
Свойства
функций
Рекомендуемое время исполнения 15 секунд
1)
(-4;-1) 2) [-4;-1]U[3;∞)
3) (-4;-1)U(3;∞)
4) (0;2)
Слайд 34
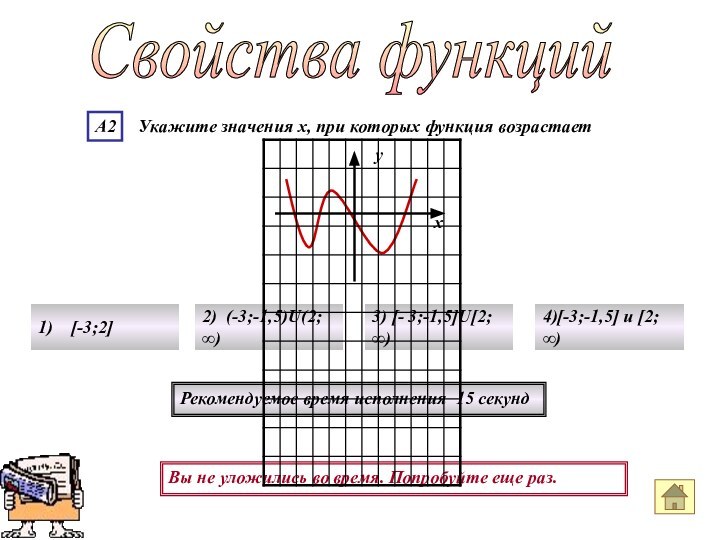
Свойства функций
Рекомендуемое время исполнения 15 секунд
1)
(-4;-1)
2) [-4;-1]U[3;∞)
3)
(-4;-1)U(3;∞) 4) (0;2)
Слайд 36
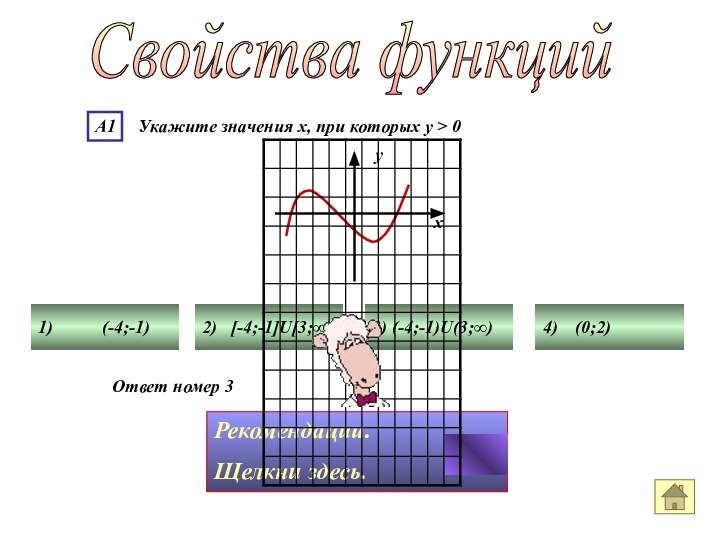
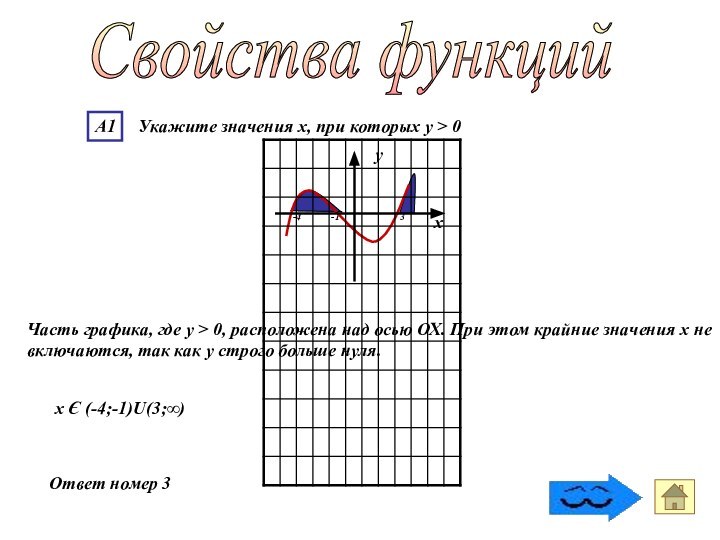
Ответ номер 3
Свойства функций
Часть графика, где у
> 0, расположена над осью ОХ. При этом крайние
значения х не включаются, так как у строго больше нуля.-4 -1 3
х Є (-4;-1)U(3;∞)
Слайд 38
Свойства функций
Рекомендуемое время исполнения 15 секунд
1)
[-3;2]
2) (-3;-1,5)U(2;∞)
3) [- 3;-1,5]U[2;∞)
4)[-3;-1,5] и
[2;∞)
Слайд 39
Вы не уложились во время. Попробуйте еще раз.
Свойства
функций
Рекомендуемое время исполнения 15 секунд
1) [-3;2]
2) (-3;-1,5)U(2;∞)
3) [- 3;-1,5]U[2;∞)
4)[-3;-1,5] и [2;∞)
Слайд 40
Свойства функций
Рекомендуемое время исполнения 15 секунд
1)
[-3;2]
2) (-3;-1,5)U(2;∞)
3) [- 3;-1,5]U[2;∞)
4)[-3;-1,5] и
[2;∞)
Слайд 41
Свойства функций
Ответ номер 4
1) [-3;2]
2) (-3;-1,5)U(2;∞)
3) [- 3;-1,5]U[2;∞)
4)[-3;-1,5] и [2;∞)
Слайд 42
Ответ номер 4
Свойства функций
Для определения промежутков монотонности
проведите по графику слева направо. Определите промежутки возрастания.
-3 -1,5 2х Є [-3;-1,5] и [2;∞)
Помните! Если промежутков несколько, то знак объединения не ставится
Слайд 44
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
2
2)
0 3) -1
4) -2
Слайд 45
Вы не уложились во время. Попробуйте еще раз.
Решение
уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
2 2) 0
3) -1
4) -2
Слайд 46
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
2
2)
0 3) -1
4) -2
Слайд 48
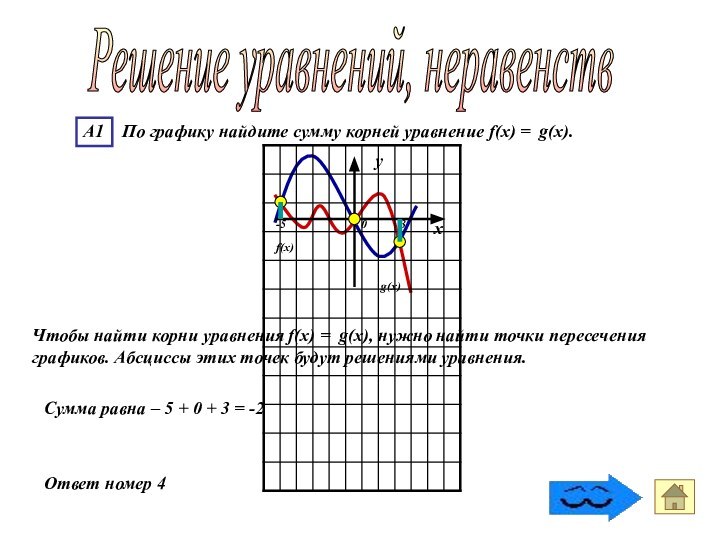
Ответ номер 4
Решение уравнений, неравенств
Чтобы найти корни
уравнения f(x) = g(x), нужно найти точки пересечения графиков.
Абсциссы этих точек будут решениями уравнения.-5 0 3
Сумма равна – 5 + 0 + 3 = -2
Слайд 50
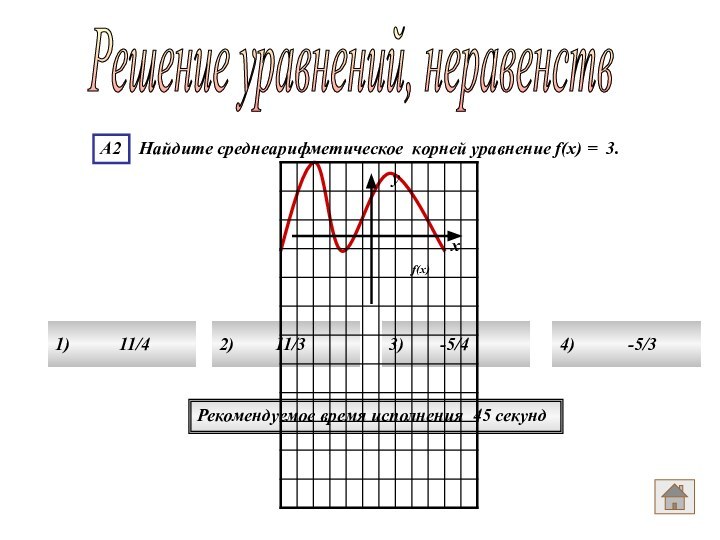
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
11/4
2)
11/3 3) -5/4
4) -5/3
f(x)
у
х
Слайд 51
Вы не уложились во время. Попробуйте еще раз.
Решение
уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
11/4 2) 11/3
3) -5/4
4) -5/3
f(x)
у
х
Слайд 52
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
11/4
2)
11/3 3) -5/4
4) -5/3
f(x)
у
х
Слайд 54
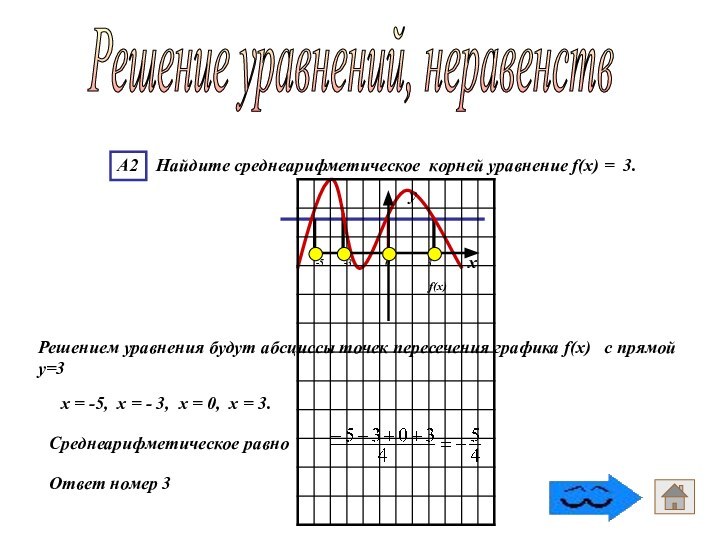
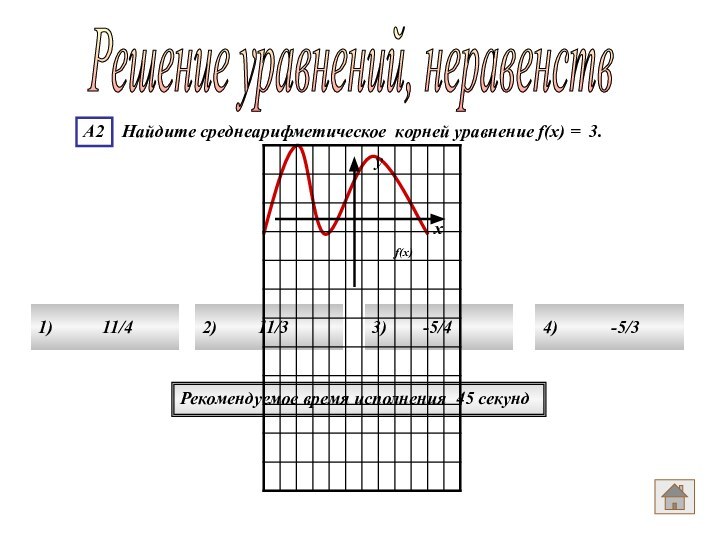
Ответ номер 3
Решение уравнений, неравенств
Решением уравнения будут
абсциссы точек пересечения графика f(x) с прямой у=3
-5
-3 0 3х = -5, х = - 3, х = 0, х = 3.
f(x)
у
х
Слайд 55
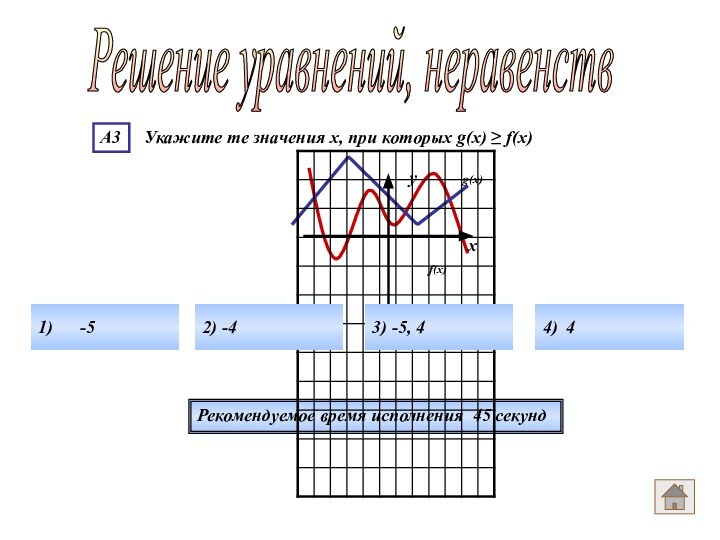
Рекомендуемое время исполнения 45 секунд
Решение уравнений, неравенств
1)
-5
2) -4
3) -5, 4
4) 4
f(x)
у
х
Слайд 57
Ответ номер 4
Решение уравнений, неравенств
Чтобы найти корни
уравнения f(x) = g(x), нужно найти точки пересечения графиков.
Абсциссы этих точек будут решениями уравнения.-5 0 3
Сумма равна – 5 + 0 + 3 = -2
Слайд 59
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
f(x)
у
х
1) -5
2) -4
3) -5, 4
4)
4
Слайд 60
Вы не уложились во время. Попробуйте еще раз.
Решение
уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
f(x)
у
х
1)
-5 2) -4
3) -5, 4
4) 4
Слайд 61
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
f(x)
у
х
1) -5
2) -4
3) -5, 4
4)
4
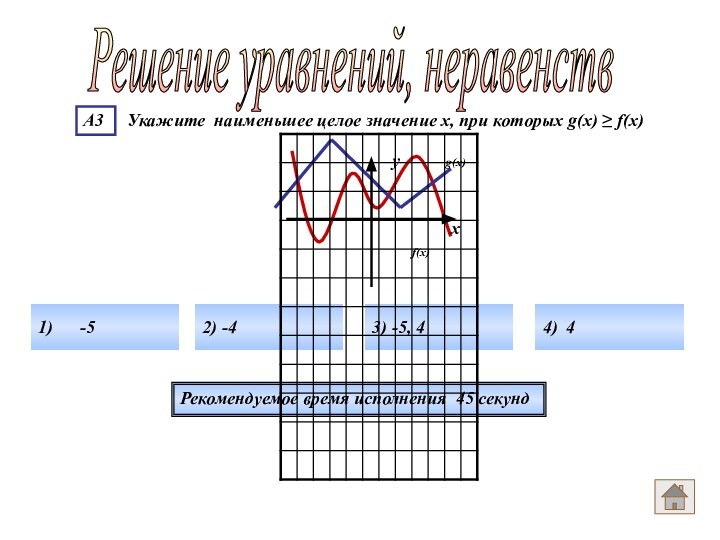
Слайд 63
Ответ номер 2
Решение уравнений, неравенств
Для того, чтобы
соблюсти условие, что g(x) ≥ f(x), надо выбрать ту
часть графика, где g(x) выше графика f(x). -5 1 4
хЄ [-5;1]U[4;∞)
f(x)
у
х
Слайд 65
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
[-5;-2]
2) (-4,5;-2]
3) (-∞;-5)U(0;3)
4) (-5;0) U(4;6)
Слайд 66
Вы не уложились во время. Попробуйте еще раз.
Решение
уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
[-5;-2] 2) (-4,5;-2]
3) (-∞;-5)U(0;3)
4) (-5;0) U(4;6)
Слайд 67
Решение уравнений, неравенств
Рекомендуемое время исполнения 45 секунд
1)
[-5;-2]
2) (-4,5;-2]
3) (-∞;-5)U(0;3)
4) (-5;0) U(4;6)
Слайд 68
Ответ номер 4
Решение уравнений, неравенств
1)
[-5;-2]
2) (-4,5;-2]
3) (-∞;-5)U(0;3)
4) (-5;0) U(4;6)
Слайд 69
Ответ номер 4
Решение уравнений, неравенств
Решением будут те
значения х, при которых график f(x) будет ниже прямой
у= -2хЄ (-5;0) U(4;6)
-6 -5 0 3
Слайд 71
Множество значений функции
Рекомендуемое время исполнения 45 секунд
1)
(-∞;0)U(0;∞)
2) (-2;2)
3) (-∞;-2]U[2;∞)
4) (-∞;-2)U(2;∞)
Слайд 72
Вы не уложились во время. Попробуйте еще раз.
Множество
значений функции
Рекомендуемое время исполнения 45 секунд
1) (-∞;0)U(0;∞)
2)
(-2;2)3) (-∞;-2]U[2;∞)
4) (-∞;-2)U(2;∞)